I denne artikel vil jeg introducere de grundlæggende principper for opretholdelse af kvalitet.

Dette omfatter kvalitetssikring, kvalitetskontrol og metrologi. Vi bruger kvalitetssikring til at få tillid til, at kvalitetskravene vil blive opfyldt. Kvalitetskontrol bruges til at kontrollere, at kravene er blevet opfyldt. Der er tale om en subtil forskel, og i praksis anvendes begreberne undertiden i flæng. Metrologi er videnskaben om måling. Det er den måde, hvorpå vi sikrer, at vi med sikkerhed kan sammenligne resultaterne af målinger, der foretages over hele verden.

Disse principper kan gælde for produkter eller en tjenesteydelse, men jeg vil fokusere på fremstilling, og hvordan disse tre grundlæggende begreber forholder sig til hinanden i den sammenhæng. Jeg har derfor undgået detaljerne i specifikke metoder, og jeg går ikke ind i nogen af de matematiske detaljer. Det gemmer jeg til en senere artikel.

Målingens oprindelse

Ægypterne brugte målestandarder med regelmæssige kalibreringer for at sikre, at stenene passede sammen i deres store byggeprojekter. Men de moderne kvalitetssystemer begyndte først rigtigt i løbet af den industrielle revolution. Før da blev mekaniske varer fremstillet af håndværkere, som finpudsede hver enkelt del individuelt, så den passede ind i en samling. Det betød, at hver maskine og hver enkelt del i den var unik. Hvis en del skulle udskiftes, skulle håndværkeren montere en ny del.

I slutningen af det 18. århundrede begyndte de franske våbenfabrikanter at fremstille musketer med standarddele. Det betød, at hæren kunne medbringe reservedele og hurtigt udskifte dem for ødelagte dele. Disse udskiftelige dele blev stadigvæk tilpasset til samlingen, men i stedet for at tilpasse hver enkelt del til den enkelte pistol, blev de tilpasset til en hoveddel .

Nogle få år senere begyndte de amerikanske våbenfabrikanter at bruge denne metode, men tilpassede den til deres uuddannede arbejdere. De filede målere til at passe til hoveddelen, og arbejderne indstillede gerigter og produktionsmaskiner ved hjælp af målere, og de brugte også målerne til at kontrollere delene. Dette gjorde det muligt for en række maskiner, der hver især udførte en enkelt operation med en ufaglært operatør, at fremstille nøjagtige dele. Disse dele kunne derefter hurtigt samles til komplekse maskiner.

Grundlaget for den moderne produktion var således blevet lagt, over 100 år før Ford ville anvende disse idéer på en bevægelig produktionslinje.

Kalibrering, sand værdi og målefejl

Et system af hoveddele, målere og maskiner til engangsbrug fungerede, da et helt produkt blev fremstillet på en enkelt fabrik. Moderne globale forsyningskæder har brug for et andet system.

I stedet for at have en fysisk masterpart har vi en tegning eller en digital CAD-model. Specificerede tolerancer sikrer, at delene passer sammen og fungerer efter hensigten. I stedet for at alle producenter kommer til en enkelt hoveddel for at indstille deres målere, får de kalibreret deres måleinstrumenter. Instrumenterne bruges derefter til at indstille produktionsmaskinerne og til at kontrollere de producerede dele.

Al kvalitet afhænger af denne kalibreringsproces.

Det vigtigste begreb at forstå er, at alle målinger har en usikkerhed. Hvis jeg bad dig om at vurdere højden af denne tekst, ville du måske sige: ” den er ca. 4 mm” . Ved at bruge ordet “ca.” antyder du, at der er en vis usikkerhed i dit skøn.

Faktisk kan vi aldrig kende den nøjagtige sande værdi af noget som helst, alle målinger er faktisk skøn, og de har en vis usikkerhed. Forskellen mellem et måleresultat og den sande værdi er målefejlen . Da vi ikke kan kende den sande værdi, kan vi heller ikke kende fejlen: det er uvisse størrelser.

Alt, hvad vi kan kvantificere om verden omkring os, er resultaterne af målinger, og disse har altid en vis usikkerhed, selv om denne usikkerhed er meget lille.

Nøjagtighed og usikkerhed. (Billedet er venligst udlånt af forfatteren.)

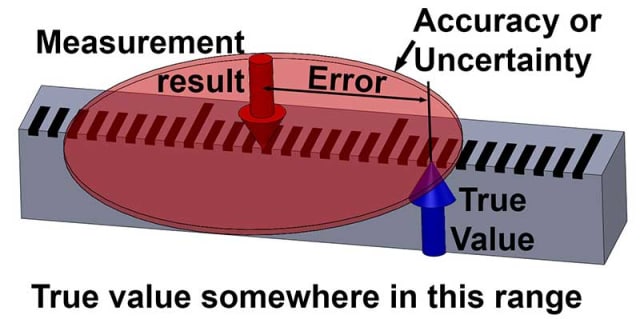
Hvis du anslår højden af denne tekst til ” ca. 4 mm, plus/minus 1 mm”, har du nu sat nogle grænser for din usikkerhed. Men du kan stadig ikke være 100 procent sikker på, at det er rigtigt.

Du kan måske have en vis grad af sikkerhed, lad os sige 95 procent, for at det er sandt. Hvis du øger grænserne, til f.eks. plus/minus 2 mm , så vil din sikkerhed stige, måske til 99 procent. Så usikkerheden giver nogle grænser, inden for hvilke vi har en vis grad af tillid til, at den sande værdi ligger.

OK, filosofiundervisningen er slut!

I et fremtidigt indlæg vil jeg uddybe disse idéer, og hvordan usikkerheden for et bestemt konfidensniveau kan beregnes.

Usikkerhed og kvalitet

Når vi har bestemt usikkerheden (eller “nøjagtigheden”) af en måling, kan vi derefter anvende denne til at afgøre, om en del overholder en bestemt tolerance. Lad os f.eks. sige, at en del er specificeret til at være 100 mm +/- 1 mm. Vi måler den og får et resultat på 100,87 mm.

Er emnet i overensstemmelse med specifikationen?

Det enkle svar er: “Vi ved det ikke, måske er den det, men måske var der en fejl i vores måling, og faktisk er delen mere end 101 mm. Måske var der en endnu større fejl, og delene er faktisk mindre end 99 mm!”

Medmindre vi ved, hvad måleusikkerheden er, har vi ingen idé om, hvor sikre vi kan være på, at delen er inden for specifikationerne. Lad os antage, at målingens usikkerhed blev angivet, så måleresultatet er 100,87 mm +/- 0,1 mm med 95 procent sikkerhed. Nu kan vi med mere end 95 % sikkerhed sige, at emnet er inden for specifikationerne.

Så forståelse og kvantificering af måleusikkerheden ved målinger er afgørende for at opretholde kvaliteten.

Lad os nu se på kalibrering og det tilhørende koncept om sporbarhed. Dette er et grundlæggende aspekt af usikkerhed. En kalibrering er en sammenligning med en reference, og usikkerheden ved denne sammenligning skal altid medtages, af de grunde, der forklares nedenfor.

En sporbar måling er en måling, som har en ubrudt kæde af kalibreringer, der går hele vejen tilbage til den primære standard. I forbindelse med målinger af længder er den primære standard definitionen af meteren, dvs. den afstand, som lys tilbagelægger i et vakuum på 1/299 792 458 sekunder, som er fastlagt af Det Internationale Bureau of Weights and Measures (BIPM) i Paris.

En måling er sporbar, hvis der er en ubrudt kæde af kalibreringer tilbage til den primære standard. (Billede venligst udlånt af forfatteren.)

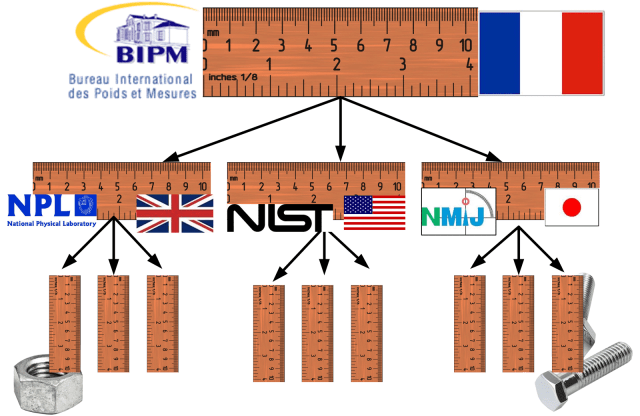
Siden 1930’erne har tomme været defineret som 25,4 mm og er derfor også sporbar til den samme meterstandard. Alle målinger skal kunne spores tilbage til den samme standard for at sikre, at dele, der er fremstillet i forskellige lande, passer sammen.

Usikkerhed og fejl

Usikkerheden ved målinger opstår fra forskellige kilder. Nogle af disse vil føre til en konsekvent fejl, eller bias, i resultatet.

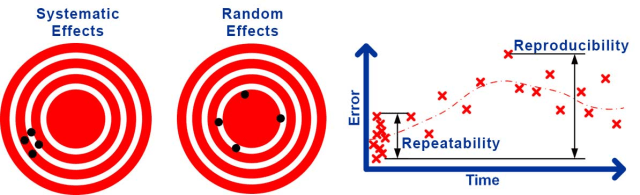
F.eks. vil den ukendte fejl, der var til stede, da et instrument blev kalibreret, føre til en konstant fejl, når det anvendes. Denne type virkning er kendt som en systematisk usikkerhed, der fører til en systematisk fejl . Andre kilder vil føre til fejl, som ændrer sig tilfældigt, hver gang der foretages en måling.

For eksempel kan turbulens i luften forårsage små, tilfældigt skiftende forstyrrelser i lasermålinger, og mekanisk spil og justering kan forårsage tilfældigt skiftende fejl i mekaniske målinger. Denne type virkning er kendt som en tilfældig usikkerhed, der fører til en tilfældig fejl .

Det er konventionelt at opdele den tilfældige usikkerhed i repeterbarhed , den tilfældige usikkerhed af resultater under de samme betingelser, og reproducerbarhed , den tilfældige usikkerhed under ændrede betingelser.

Selvfølgelig kan betingelserne aldrig være nøjagtigt ens eller helt forskellige, så sondringen er noget uklar. De typer af betingelser, der kan ændres, er at foretage målingen på et andet tidspunkt, med en anden operatør, et andet instrument, ved hjælp af en anden kalibrering og i et andet miljø.

Systematiske vs. tilfældige effekter. (Billedet er venligst udlånt af forfatteren.)

Der findes to almindeligt anvendte metoder til at kvantificere usikkerheden ved en måling. Kalibreringslaboratorier og videnskabelige institutioner udfører normalt usikkerhedsvurdering i henhold til Guide to the Expression of Uncertainty in Measurement (GUM) .

GUM-metoden indebærer, at man først tager hensyn til alle de påvirkninger, der kan påvirke måleresultatet. Derefter skal der fastlægges en matematisk model, som giver måleresultatet som en funktion af disse påvirkende størrelser. Ved at tage hensyn til usikkerheden i hver enkelt inputmængde og anvende “loven om usikkerhedens udbredelse” kan der beregnes et estimat for den samlede usikkerhed ved målingen.

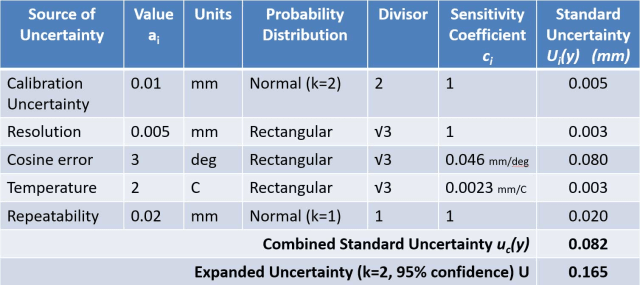
GUM-tilgangen beskrives undertiden som bottom-up , da den starter med en betragtning af hver enkelt påvirkning. Hver påvirkning er normalt opført i en tabel, der kaldes et usikkerhedsbudget, som bruges til at beregne den kombinerede usikkerhed.

Eksempel på usikkerhedsbudget. (Billedet er venligst stillet til rådighed af forfatteren.)

Industrielle måleprocesser evalueres typisk ved hjælp af en Measurement Systems Analysis (MSA)-tilgang, som anbefalet inden for Six-Sigma-metodologien og normalt efter retningslinjerne i Automotive Industry Action Group (AIAG) MSA Reference Manual .

MSA indebærer udførelse af måleundersøgelser, hvor gentagne målinger sammenlignes med en reference under forskellige betingelser for at bestemme bias, repeterbarhed og undertiden reproducerbarhed.

En type-1 måleundersøgelse er den hurtige kontrol, der normalt udføres for i første omgang at forstå variationen i en måle. Det indebærer, at en enkelt operatør måler en enkelt kalibreret referencedel 25 eller flere gange og derefter vurderer variationen og bias i resultaterne. Denne type test kaldes ofte en repeterbarhedsundersøgelse uden for MSA.

En undersøgelse af gentagelighed og reproducerbarhed af måleinstrumenter (Gage R&R) bruges til at få en mere detaljeret forståelse af en måleproces. Typisk måles 10 dele hver to gange af mindst tre forskellige operatører. Derefter anvendes en statistisk teknik kaldet ANOVA til at bestemme, hvor meget variation der skyldes instrumentet (“måleinstrumentet”), og hvor meget der skyldes operatøren. Hermed anses skiftet af operatør og efterfølgende ændringer i tid og miljø for at være en fuldstændig repræsentation af reproducerbarhedsforholdene.

MSA betegnes undertiden som top-down, da den i vid udstrækning behandler måleprocessen som en black-box og eksperimentelt bestemmer systematiske og tilfældige usikkerheder. To vigtige begreber i MSA er nøjagtighed , der anvendes som ækvivalent for usikkerhed, og præcision , der anvendes som ækvivalent for tilfældig usikkerhed.

Fordelen ved usikkerhedsevaluering er, at den er i stand til at tage hensyn til alle usikkerhedskilder og, hvis den udføres korrekt, giver det mest nøjagtige skøn over usikkerheden. Problemerne ved denne fremgangsmåde er bl.a., at den kræver en metrolog, der er i stand til at udarbejde den matematiske model, og at der er risiko for menneskelige fejl, der fører til, at væsentlige påvirkninger udelades eller vurderes forkert.

GUM-metoden er også kun gyldig for en individuel måling, som er udført med kendte værdier for eventuelle anvendte korrektioner. Det er derfor vanskeligt at anvende usikkerhedsvurderingen korrekt til at forudsige usikkerheden i en industriel måleproces.

MSA kan anvendes meget lettere og er beregnet til at give en forudsigelse af nøjagtigheden af en industriel måleproces. Problemet med denne fremgangsmåde er, at der ikke tages hensyn til visse systematiske virkninger, og at reproducerbarhedsbetingelser måske ikke er fuldt ud repræsenteret, hvilket fører til en undervurdering af usikkerheden.

Et eksempel på udeladelse af systematiske virkninger er, at der ved bestemmelse af bias foretages en sammenligning med en reference, som behandles som den sande værdi – i virkeligheden har referencen også en usikkerhed, som bør medtages. Denne metode er baseret på, at alle reproducerbarhedsbetingelser varieres, således at deres virkninger kan ses i variationen af resultaterne ved gentagne målinger. Det er sandsynligt, at den måde, hvorpå disse betingelser varieres, ikke fuldt ud vil afspejle den variation, der ses i løbet af den faktiske måleproces.

Måling og kvalitetssikring

Indtil videre har jeg fokuseret på kvalitetskontrol, dvs. hvordan målinger kan bevise, at dele er i overensstemmelse med specifikationerne, efter at de er blevet produceret. Lad os nu kort se på kvalitetssikring, dvs. den måde, hvorpå vi sikrer, at processen overhovedet producerer gode dele.

Dette aspekt af kvalitet behandles i vid udstrækning af statistisk processtyring (SPC) . En proces kan evalueres ved at fremstille flere dele og måle dem for at bestemme variationen og skævheden i fremstillingsprocessen. I stedet for at give disse resultater direkte, er det normalt at dividere deletolerancen med procespræcisionen for at få værktøjsmaskinekapaciteten ( C P ) eller med procesnøjagtigheden for at få proceskapaciteten ( C PK ).

SPC svarer på mange måder til MSA. Den anvender en top-down-tilgang for at forstå tilfældige og systematiske virkninger. I stedet for at evaluere målinger anvendes den imidlertid til at evaluere procesoutput. Den har generelt de samme fordele og ulemper som MSA, og der kan anvendes en bottom-up tilgang til usikkerhedsevaluering, hvis disse er et problem.

Det kan umiddelbart se ud til, at der er grundlæggende forskelle mellem MSA og SPC på grund af den meget forskellige terminologi inden for SPC. Variation af almindelig årsag (eller variation af tilfældig årsag i ældre litteratur) svarer imidlertid til præcision; korttidsvariabilitet svarer til repeterbarhed; langtidsvariabilitet svarer til reproducerbarhed; og variation af særlig årsag (eller variation af henførbar årsag i ældre litteratur) svarer til bias.

SPC lægger også meget større vægt på at sikre, at en proces er under “statistisk kontrol”. I store træk betyder dette, at virkningerne er tilfældige og normalfordelte, og at der er korrigeret for eventuelle væsentlige systematiske virkninger. Dette er et af SPC’s stærke punkter, som nogle gange overses i både usikkerhedsevaluering og MSA.

Det vigtigste værktøj, der anvendes i SPC til at kontrollere, om en proces er “under kontrol”, er kontroldiagrammet . Dette giver en enkel grafisk visning af en proces, hvor det er let at se, hvornår en proces er ved at glide eller producerer fejl, som ikke kan forklares ved normale tilfældige variationer. Hvis f.eks. flere punkter alle er stigende eller faldende, tyder det på, at processen er ved at glide.

Eksempel på kontroldiagram. (Billedet er venligst udlånt af forfatteren.)

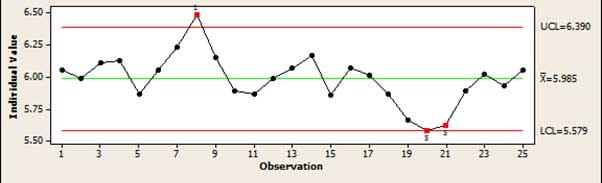
I denne artikel har jeg forsøgt at give et bredt overblik over et stort og komplekst emne. Jeg har introduceret de grundlæggende principper bag opretholdelse af kvalitet uden at komme ind på den matematik, der er nødvendig for at anvende disse metoder.

Hold øje med fremtidige artikler om disse emner.

Dr. Jody Muelaners 20-årige ingeniørkarriere begyndte med maskinkonstruktion, hvor han arbejdede på alt fra medicinsk udstyr til savværker. Siden 2007 har han udviklet ny metrologi på University of Bath i tæt samarbejde med førende virksomheder inden for luft- og rumfart. Denne forskning er i øjeblikket fokuseret på usikkerhedsmodellering af produktionssystemer, hvor elementer af SPC, MSA og metrologi kombineres med nye numeriske metoder. Han interesserer sig også for cykeldesign. Besøg hans websted for at få flere oplysninger.