Forskellige topologier for en forstærker med negativ tilbagekobling, der anvender to porte. Øverst til venstre: topologi med strømforstærker; øverst til højre: transkonduktans; nederst til venstre: transresistens; nederst til højre: topologi med spændingsforstærker.

Som nævnt i afsnittet Signalstrømsanalyse er en form for signalstrømsanalyse den mest generelle måde at behandle en negativ-feedbackforstærker på, men repræsentation som to to-porte er den fremgangsmåde, der oftest præsenteres i lærebøger og præsenteres her. Den bibeholder en opdeling af forstærkeren i to blokke, men tillader, at blokkene kan være bilaterale. Nogle ulemper ved denne metode er beskrevet til sidst.

Elektroniske forstærkere anvender strøm eller spænding som ind- og udgang, så der er fire typer forstærkere mulige (en af to mulige indgange med en af to mulige udgange). Se klassifikation af forstærkere. Målet for feedbackforstærkeren kan være en hvilken som helst af de fire forstærkertyper og er ikke nødvendigvis af samme type som open-loop-forstærkeren, som selv kan være en hvilken som helst af disse typer. Så f.eks. kan en op-forstærker (spændingsforstærker) arrangeres til at lave en strømforstærker i stedet.

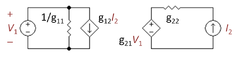
Negativ-feedback-forstærkere af enhver type kan gennemføres ved hjælp af kombinationer af to-portnetværk. Der findes fire typer af toportsnetværk, og den ønskede forstærkertype dikterer valget af toporte og valget af en af de fire forskellige forbindelsestopologier, der er vist i diagrammet. Disse forbindelser betegnes normalt som serie- eller shuntforbindelser (parallelforbindelser). I diagrammet viser den venstre kolonne shunt-indgange; den højre kolonne viser serieindgange. Den øverste række viser serieudgange; den nederste række viser shuntudgange. De forskellige kombinationer af forbindelser og to porte er anført i nedenstående tabel.

VCVS

Til eksempel, for en forstærker med strømtilbagekobling samples strømmen fra udgangen med henblik på tilbagekobling og kombineres med strømmen ved indgangen. Derfor udføres tilbagekoblingen ideelt set ved hjælp af en (udgangs)strømstyret strømkilde (CCCS), og dens ufuldkomne realisering ved hjælp af et toportnetværk skal også indeholde en CCCS, dvs. det hensigtsmæssige valg for tilbagekoblingsnetværk er et g-parameter toportnetværk. Her præsenteres den to-port-metode, der anvendes i de fleste lærebøger, ved hjælp af det kredsløb, der behandles i artiklen om asymptotisk forstærkningsmodel.

Figur 3: En shunt-series feedbackforstærker

Figur 3 viser en to-transistorforstærker med en feedbackmodstand Rf. Formålet er at analysere dette kredsløb for at finde tre elementer: forstærkningen, udgangsimpedansen, når man ser ind i forstærkeren fra belastningen, og indgangsimpedansen, når man ser ind i forstærkeren fra kilden.

Udskiftning af tilbagekoblingsnetværket med et to-portRediger

Det første skridt er udskiftning af tilbagekoblingsnetværket med et to-port. Hvilke komponenter indgår i en toport?

På indgangssiden af en toport har vi Rf. Hvis spændingen på højre side af Rf ændres, ændrer det den strøm i Rf, der trækkes fra den strøm, der kommer ind i indgangstransistorens base. Det vil sige, at indgangssiden af toporten er en afhængig strømkilde, der styres af spændingen ved toppen af modstand R2.

Man kan sige, at forstærkerens andet trin blot er en spændingsfølger, der overfører spændingen ved indgangstransistorens kollektor til toppen af R2. Det vil sige, at det overvågede udgangssignal i virkeligheden er spændingen ved kollektoren af indgangstransistoren. Dette synspunkt er legitimt, men så bliver spændingsfølgertrinnet en del af tilbagekoblingsnetværket. Det gør analysen af tilbagekoblingen mere kompliceret.

Figur 4: G-parameterens tilbagekoblingsnetværk

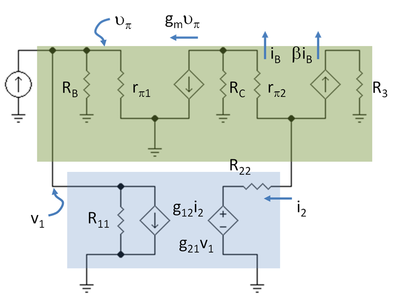
En alternativ opfattelse er, at spændingen i toppen af R2 indstilles af emitterstrømmen fra udgangstransistoren. Denne opfattelse fører til et helt passivt tilbagekoblingsnetværk bestående af R2 og Rf. Den variabel, der styrer tilbagekoblingen, er emitterstrømmen, så tilbagekoblingen er en strømstyret strømkilde (CCCS). Vi gennemgår de fire tilgængelige toportnetværk og finder, at det eneste netværk med en CCCS er det g-parameterbaserede toportnetværk, der er vist i figur 4. Den næste opgave er at vælge g-parametrene, således at to-porten i figur 4 er elektrisk ækvivalent med L-afsnittet bestående af R2 og Rf. Denne udvælgelse er en algebraisk procedure, som er meget enkel ved at se på to individuelle tilfælde: tilfældet med V1 = 0, som gør VCVS på højre side af toporten til en kortslutning, og tilfældet med I2 = 0, som gør CCCS på venstre side til et åbent kredsløb. Algebraen i disse to tilfælde er enkel, meget lettere end at løse for alle variabler på en gang. Valget af g-parametre, der får to-porten og L-afsnittet til at opføre sig ens, er vist i nedenstående tabel.

– R 2 R 2 + R f {\displaystyle -{\frac {R_{2}}{R_{2}}{R_{2}+R_{\mathrm {f} }}}}

R 2 R 2 2 + R f {\displaystyle {\frac {R_{2}}}{R_{{2}+R_{\mathrm {f} }}}}

g11	g12	g21	g22
1 R f + R 2 {\displaystyle {\frac {\frac {1}{R_{\mathrm {f} }+R_{2}}}}	R 2 / / R f {\displaystyle R_{2}//R_{{\mathrm {f} }\ }

Figur 5: Små signalkredsløb med to-port til tilbagekoblingsnetværk; øverste skraverede kasse: hovedforstærker; nederste skraverede kasse: tilbagekoblet to-port, der erstatter L-afsnittet bestående af Rf og R2.

Små signalkredsløbRediger

Det næste skridt er at tegne småsignalskemaet for forstærkeren med toporten på plads ved hjælp af hybrid-pi-modellen for transistorerne. Figur 5 viser skemaet med notation R3 = RC2 // RL og R11 = 1 / g11, R22 = g22.

Belastet open-loop gainEdit

Figur 3 angiver udgangsknudepunktet, men ikke valget af udgangsvariabel. Et nyttigt valg er forstærkerens kortslutningsstrømsudgang (hvilket fører til kortslutningsstrømsforstærkning). Da denne variabel ganske enkelt fører til et af de andre valg (f.eks. belastningsspænding eller belastningsstrøm), findes kortslutningsstrømsforstærkningen nedenfor.

Først findes den belastede open-loop-forstærkning. Tilbagekoblingen slukkes ved at indstille g12 = g21 = 0. Ideen er at finde ud af, hvor meget forstærkerforstærkningen ændres på grund af modstandene i tilbagekoblingsnetværket i sig selv, med tilbagekoblingen slået fra. Denne beregning er ret nem, fordi R11, RB og rπ1 alle er parallelle, og v1 = vπ. Lad R1 = R11 // RB // rπ1. Desuden er i2 = -(β+1) iB. Resultatet for open-loop strømforstærkning AOL er:

A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\displaystyle A_{\mathrm {OL} }={\\frac {\beta i_{\mathrm {B} }}}{i_{{\mathrm {S}} }}}}=g_{{m}R_{\mathrm {C}} }\left({\frac {\beta }{\beta +1}}}\right)\left({\frac {R_{1}}}{R_{22}+{\frac {r_{{\pi 2}+R_{{{mathrm {C} }}}{\beta +1}}}}\right)\ .}

Forstærkning med feedbackRediger

I den klassiske tilgang til feedback negligeres den feedforward, der repræsenteres af VCVS (dvs. g21 v1). Det får kredsløbet i figur 5 til at ligne blokdiagrammet i figur 1, og forstærkningen med feedback er så:

A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB} }={\\frac {A_{{\mathrm {OL}} }}}{1+{\beta }_{{\mathrm {FB}} }A_{{\mathrm {OL}} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{{\mathrm {FB}} }={\\frac {A_{{\mathrm {OL} }}}{1+{{\frac {R_{2}}}{R_{2}+R_{\mathrm {f} }}}}A_{{\mathrm {OL}} }}}}}\} ,}

hvor feedbackfaktoren βFB = -g12. Notationen βFB er indført for feedbackfaktoren for at skelne den fra transistoren β.

Indgangs- og udgangsmodstandeRediger

Figur 6: Kredsløbsopsætning til bestemmelse af feedbackforstærkerens indgangsmodstand

Feedback anvendes til bedre at tilpasse signalkilderne til deres belastninger. F.eks. kan en direkte tilslutning af en spændingskilde til en resistiv belastning resultere i signaltab på grund af spændingsdeling, men ved at indskyde en negativ feedbackforstærker kan man øge den tilsyneladende belastning, der ses af kilden, og reducere den tilsyneladende driverimpedans, der ses af belastningen, hvorved man undgår signaldæmpning på grund af spændingsdeling. Denne fordel er ikke begrænset til spændingsforstærkere, men analoge forbedringer af tilpasningen kan arrangeres for strømforstærkere, transkonduktansforstærkere og transmodstandsforstærkere.

For at forklare disse virkninger af feedback på impedanserne skal der først foretages en digression om, hvordan to-portsteorien nærmer sig modstandsbestemmelse, og derefter dens anvendelse på den foreliggende forstærker.

Baggrund for modstandsbestemmelseRediger

Figur 6 viser et ækvivalentkredsløb til bestemmelse af indgangsmodstanden for en tilbagekoblet spændingsforstærker (til venstre) og for en tilbagekoblet strømforstærker (til højre). Disse opstillinger er typiske anvendelser af Miller-sætningen.

I spændingsforstærkerens tilfælde påføres udgangsspændingen βVout fra det tilbagekoblede netværk i serie og med modsat polaritet i forhold til den indgangsspænding Vx, der løber over sløjfen (men i forhold til jord er polariteterne de samme). Som følge heraf falder den effektive spænding over og strømmen gennem forstærkerens indgangsmodstand Rin, således at kredsløbets indgangsmodstand stiger (man kan sige, at Rin tilsyneladende stiger). Dens nye værdi kan beregnes ved at anvende Miller-teoremet (for spændinger) eller de grundlæggende kredsløbslove. Således giver Kirchhoffs spændingslov:

V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} }+\beta v_{{\mathrm {out} }\ ,}

hvor vout = Av vin = Av Ix Rin. Ved at indsætte dette resultat i ovenstående ligning og løse for feedbackforstærkerens indgangsmodstand er resultatet:

R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {\displaystyle R_{\mathrm {in} }(fb)={{\frac {V_{x}}}{I_{x}}}=\left(1+\beta A_{v}\right)R_{\mathrm {in} }\ .}

Den generelle konklusion af dette eksempel og et lignende eksempel for udgangsmodstandstilfældet er: En seriefeedbackforbindelse ved indgangen (udgangen) øger indgangs- (udgangs) modstanden med en faktor ( 1 + β AOL ), hvor AOL = forstærkning af åben sløjfe.

På den anden side, for strømforstærkeren, tilføres udgangsstrømmen βIout fra feedbacknetværket parallelt og med modsat retning af indgangsstrømmen Ix. Som følge heraf øges den samlede strøm, der løber gennem kredsløbets indgang (ikke kun gennem indgangsmodstanden Rin), og spændingen over den falder, således at kredsløbets indgangsmodstand falder (Rin falder tilsyneladende). Dens nye værdi kan beregnes ved at anvende det dobbelte Miller-teorem (for strømme) eller de grundlæggende Kirchhoff-love:

I x = V i n R i n + β i o u t . {\displaystyle I_{x}={\frac {V_{{\mathrm {in} }}{R_{{{\mathrm {in}} }}}}+\beta i_{{\mathrm {out}} }\ .}

hvor iout = Ai iin = Ai Vx / Rin. Ved at indsætte dette resultat i ovenstående ligning og løse for feedbackforstærkerens indgangsmodstand er resultatet:

R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}}{I_{x}}}={\frac {R_{{{mathrm {in}} }}}{{\left(1+\beta A_{i}\right)}}\ .}

Den generelle konklusion fra dette eksempel og et lignende eksempel for udgangsmodstandstilfælde er: En parallel feedbackforbindelse ved indgangen (udgangen) reducerer indgangs- (udgangs) modstanden med en faktor ( 1 + β AOL ), hvor AOL = forstærkning af åben sløjfe.

Disse konklusioner kan generaliseres til at behandle tilfælde med vilkårlige Norton- eller Thévenin-drev, vilkårlige belastninger og generelle feedbacknetværk med to porte. Resultaterne afhænger imidlertid af, at hovedforstærkeren er repræsenteret som en to-port – dvs. at resultaterne afhænger af, at den samme strøm går ind og ud af indgangsterminalerne, og på samme måde skal den samme strøm, der forlader den ene udgangsterminal, gå ind i den anden udgangsterminal.

En bredere konklusion, der er uafhængig af de kvantitative detaljer, er, at feedback kan bruges til at øge eller mindske indgangs- og udgangsimpedansen.

Anvendelse på eksempelforstærkerenRediger

Disse modstandsresultater anvendes nu på forstærkeren i figur 3 og figur 5. Den forbedringsfaktor, der reducerer forstærkningen, nemlig ( 1 + βFB AOL), bestemmer direkte virkningen af tilbagekoblingen på forstærkerens indgangs- og udgangsresistanser. I tilfælde af en shuntforbindelse reduceres indgangsimpedansen med denne faktor, og i tilfælde af en serieforbindelse multipliceres impedansen med denne faktor. Den impedans, der ændres af tilbagekoblingen, er imidlertid forstærkerens impedans i figur 5 med tilbagekoblingen slået fra, og den omfatter de ændringer af impedansen, der skyldes modstandene i tilbagekoblingsnetværket.

Dermed er den indgangsimpedans, der ses af kilden med tilbagekoblingen slået fra, Rin = R1 = R11 // RB // rπ1, og med tilbagekoblingen slået til (men ingen feedforward)

R i n = R 1 1 1 + β F B A O L , {\displaystyle R_{\mathrm {in} }={\\frac {R_{1}}}{1+{\beta }_{\mathrm {FB} }A_{{{\mathrm {OL}} }}}}}\ ,}

hvor division anvendes, fordi indgangsforbindelsen er shunt: den tilbagekoblede to-port er parallel med signalkilden på indgangssiden af forstærkeren. En påmindelse: AOL er den belastede open loop gain fundet ovenfor, som modificeret af modstandene i tilbagekoblingsnetværket.

Den impedans, der ses af belastningen, kræver yderligere diskussion. Belastningen i figur 5 er forbundet med udgangstransistorens kollektor og er derfor adskilt fra forstærkerens krop af den uendelige impedans i udgangsstrømskilden. Derfor har tilbagekobling ingen virkning på udgangsimpedansen, som fortsat blot er RC2, som den ses af belastningsmodstanden RL i figur 3.

Hvis vi i stedet ville finde den impedans, der præsenteres ved udgangstransistorens emitter (i stedet for dens kollektor), som er serieforbundet med tilbagekoblingsnetværket, ville tilbagekobling øge denne modstand med forbedringsfaktoren ( 1 + βFB AOL).

Belastningsspænding og belastningsstrømRediger

Den forstærkning, der er afledt ovenfor, er strømforstærkningen ved udgangstransistorens kollektor. For at relatere denne forstærkning til forstærkningen, når spændingen er forstærkerens udgang, skal man bemærke, at udgangsspændingen ved belastningen RL er relateret til kollektorstrømmen ved Ohm’s lov som vL = iC (RC2 || RL). Følgelig findes transmodstandsforstærkningen vL / iS ved at multiplicere strømforstærkningen med RC2 || RL:

v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{\mathrm {L} }}}{i_{{\mathrm {S}} }}}}=A_{{\mathrm {FB}} }(R_{{\mathrm {C2} }\parallel R_{\mathrm {L} })\ .}

Såfremt forstærkerens udgang antages at være strømmen i belastningsmodstanden RL, bestemmer strømdivisionen belastningsstrømmen, og forstærkningen er så:

i L i S = A F B R C 2 R C 2 R C 2 + R L . {\displaystyle {\frac {i_{{\mathrm {L} }}}{i_{\mathrm {S}}{i_{\mathrm {S}}}{i_{\mathrm {S}} }}}}=A_{{\mathrm {FB}}=A_{\mathrm {FB} }{\frac {R_{{\mathrm {C2}} }}{R_{{\mathrm {C2}}{R_{{\mathrm {C2}}{R_{\mathrm {C2} }+R_{{\mathrm {L}}+R_{{\mathrm {L}}+R_{\mathrm {L}}} }}}\ .}

Er hovedforstærkerblokken en to-port?Edit

Figur 7: Forstærker med jordforbindelser mærket med G. Tilbagekoblingsnetværket opfylder portbetingelserne.

Der følger nogle ulemper ved fremgangsmåden med to to toporte, beregnet til den opmærksomme læser.

Figur 7 viser småsignalskemaet med hovedforstærkeren og den tilbagekoblede toport i skraverede kasser. Den tilbagekoblede to-port opfylder portbetingelserne: ved indgangsporten kommer Iin ind og forlader porten, og ligeledes ved udgangen kommer Iout ind og forlader den.

Er hovedforstærkerblokken også en to-port? Hovedforstærkeren er vist i den øverste skraverede boks. Jordforbindelserne er mærket. Figur 7 viser det interessante forhold, at hovedforstærkeren ikke opfylder portbetingelserne ved sin indgang og udgang, medmindre jordforbindelserne vælges således, at dette sker. På indgangssiden er f.eks. den strøm, der kommer ind i hovedforstærkeren, IS. Denne strøm fordeles på tre måder: til tilbagekoblingsnetværket, til forspændingsmodstanden RB og til indgangstransistorens basismodstand rπ. For at opfylde portbetingelsen for hovedforstærkeren skal alle tre komponenter returneres til hovedforstærkerens indgangsside, hvilket betyder, at alle jordledninger mærket G1 skal være forbundet, samt emitterledning GE1. På samme måde skal alle jordforbindelser G2 være tilsluttet på udgangssiden, og ligeledes jordforbindelse GE2. Derefter er G1 nederst i skemaet, under feedback to-porten og uden for forstærkerblokkene, forbundet med G2. Det tvinger jordstrømmene til at fordele sig mellem ind- og udgangssiden som planlagt. Bemærk, at dette forbindelsesarrangement opdeler emitteren af indgangstransistoren i en baseside og en kollektorside – en fysisk umulig ting at gøre, men elektrisk set ser kredsløbet alle jordforbindelser som ét knudepunkt, så denne fiktion er tilladt.

Den måde, jordledningerne er forbundet på, gør naturligvis ingen forskel for forstærkeren (de er alle ét knudepunkt), men det gør en forskel for portforholdene. Denne kunstighed er en svaghed ved denne fremgangsmåde: portbetingelserne er nødvendige for at retfærdiggøre metoden, men kredsløbet er i virkeligheden upåvirket af, hvordan strømmene handles mellem jordforbindelserne.

Men hvis ingen mulig opstilling af jordbetingelserne fører til portbetingelserne, opfører kredsløbet sig måske ikke på samme måde. Forbedringsfaktorerne (1 + βFB AOL) til bestemmelse af ind- og udgangsimpedans virker måske ikke. Denne situation er akavet, fordi en manglende mulighed for at lave en toport kan afspejle et reelt problem (det er bare ikke muligt) eller afspejle mangel på fantasi (f.eks. tænkte man bare ikke på at dele emitterknuden i to). Som følge heraf er der, når der er tvivl om portforholdene, mindst to tilgange til at fastslå, om forbedringsfaktorerne er korrekte: enten simulere et eksempel ved hjælp af Spice og sammenligne resultaterne med brugen af en forbedringsfaktor, eller beregne impedansen ved hjælp af en testkilde og sammenligne resultaterne.

Et mere praktisk valg er at droppe to-port-tilgangen helt og bruge forskellige alternativer baseret på signalflowgrafteori, herunder Rosenstark-metoden, Choma-metoden og brugen af Blackmans sætning. Dette valg kan være tilrådeligt, hvis enhedsmodeller med små signaler er komplekse eller ikke er tilgængelige (f.eks. hvis enhederne kun er kendt numerisk, måske fra målinger eller fra SPICE-simuleringer).