#InsideRL

I ett typiskt Reinforcement Learning (RL)-problem finns det en inlärare och en beslutsfattare som kallas agent, och den omgivning som den interagerar med kallas miljö. Miljön ger i gengäld belöningar och ett nytt tillstånd baserat på agentens handlingar. Vid förstärkningsinlärning lär vi alltså inte agenten hur den ska göra något, utan ger den positiva eller negativa belöningar på grundval av dess handlingar. Vår grundfråga för den här bloggen är alltså hur vi matematiskt formulerar ett problem inom RL. Det är här Markov Decision Process (MDP) kommer in.

För att kunna besvara vår grundläggande fråga, dvs. Hur vi formulerar RL-problem matematiskt (med hjälp av MDP), måste vi utveckla vår intuition om :

• Relationen mellan agent och miljö
• Markovegenskap
• Markovprocess och Markovkedjor
• Markovbelöningsprocess (MRP)
• Bellmanekvation
• Markovbelöningsprocess

Hämta ditt kaffe och sluta inte förrän du är stolt!🧐

Relationen mellan agent och miljö

Först ska vi titta på några formella definitioner :

Agent : Programvaruprogram som fattar intelligenta beslut och de är de lärande i RL. Dessa agenter interagerar med miljön genom handlingar och får belöningar baserade på sina handlingar.

Miljö :Det är demonstrationen av det problem som skall lösas.Nu kan vi ha en verklig miljö eller en simulerad miljö som vår agent kommer att interagera med.

State : Detta är agenternas position vid ett visst tidssteg i miljön.Så när en agent utför en handling ger miljön agenten en belöning och ett nytt tillstånd som agenten nådde genom att utföra handlingen.

Allt som agenten inte kan ändra godtyckligt anses vara en del av miljön. Enkelt uttryckt kan åtgärder vara alla beslut som vi vill att agenten ska lära sig och tillstånd kan vara allt som kan vara användbart vid val av åtgärder. Vi utgår inte från att allt i miljön är okänt för agenten, till exempel anses belöningsberäkningen vara en del av miljön även om agenten vet en del om hur dess belöning beräknas som en funktion av dess handlingar och de tillstånd i vilka de utförs. Detta beror på att belöningar inte kan ändras godtyckligt av agenten. Ibland kan agenten vara fullt medveten om sin omgivning men ändå ha svårt att maximera belöningen, precis som när vi vet hur man spelar Rubiks kub men ändå inte kan lösa den. Så vi kan lugnt säga att förhållandet mellan agent och omgivning representerar gränsen för agentens kontroll och inte dess kunskap.

The Markov Property

Transition : Att flytta från ett tillstånd till ett annat kallas för Transition.

Transition Probability: Sannolikheten för att agenten kommer att flytta från ett tillstånd till ett annat kallas övergångssannolikhet.

Markovs egenskap säger att :

”Framtiden är oberoende av det förflutna givet nuet”

Matematiskt kan vi uttrycka detta påstående som :

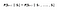
S betecknar agentens nuvarande tillstånd och s betecknar nästa tillstånd. Vad denna ekvation innebär är att övergången från tillstånd S till S är helt oberoende av det förflutna. RHS i ekvationen betyder alltså samma sak som LHS om systemet har en Markov-egenskap. Intuitivt betyder det att vårt nuvarande tillstånd redan fångar informationen om de tidigare tillstånden.

Sannolikhet för övergång av tillstånd :

Som vi nu vet om övergångssannolikhet kan vi definiera sannolikhet för övergång av tillstånd på följande sätt :

För Markovtillstånd från S till S dvs. varje annat efterföljande tillstånd , är sannolikheten för övergång av tillstånd given av

Vi kan formulera sannolikheten för övergång av tillstånd till en matris för sannolikhet för övergång av tillstånd genom :

Varje rad i matrisen representerar sannolikheten för att vi ska flytta oss från vårt ursprungliga tillstånd eller starttillstånd till något efterföljande tillstånd.Summan av varje rad är lika med 1.

Markovprocess eller Markovkedjor

Markovprocessen är den minnesfria slumpmässiga processen, dvs. en sekvens av ett slumpmässigt tillstånd S,S,….S med en Markovegenskap.Så det är i princip en sekvens av tillstånd med Markovegenskapen.Den kan definieras med hjälp av en uppsättning tillstånd (S) och en matris för sannolikhet för övergång (P).Miljöns dynamik kan definieras fullt ut med hjälp av tillstånden(S) och övergångssannolikhetsmatrisen(P).

Men vad betyder slumpmässig process ?

För att besvara denna fråga tittar vi på ett exempel:

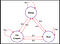
Trädets kanter anger övergångssannolikheten. Från denna kedja tar vi ett urval. Anta nu att vi sov och att det enligt sannolikhetsfördelningen finns en 0,6 chans att vi springer och 0,2 chans att vi sover mer och återigen 0,2 att vi äter glass. På samma sätt kan vi tänka oss andra sekvenser som vi kan ta stickprov från denna kedja.

Vissa stickprov från kedjan :

Sömn – Löpning – Glass – Sömn

Sömn – Glass – Glass – Löpning

I de två sekvenserna ovan ser vi att vi får slumpmässiga uppsättningar av tillstånd (S) (dvs. Sömn,Glass,Sömn ) varje gång vi kör kedjan.Hoppas att det nu står klart varför Markovprocessen kallas för en slumpmässig uppsättning sekvenser.

För att gå till Markovbelöningsprocessen ska vi titta på några viktiga begrepp som kommer att hjälpa oss att förstå MRP.

Belöning och återvändande

Belöning är de numeriska värden som agenten erhåller när han/hon utför en viss handling i ett visst tillstånd i omgivningen. Det numeriska värdet kan vara positivt eller negativt baserat på agentens handlingar.

I förstärkningsinlärning bryr vi oss om att maximera den kumulativa belöningen (alla belöningar som agenten får från miljön) i stället för den belöning som agenten får från det aktuella tillståndet (även kallad omedelbar belöning). Denna totala summa av den belöning som agenten får från omgivningen kallas avkastning.

Vi kan definiera Returns som :

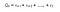
r är den belöning som agenten erhåller vid tidssteget t medan han eller hon utför en handling (a) för att gå från ett tillstånd till ett annat. På samma sätt är r den belöning som agenten får vid tidssteg t genom att utföra en åtgärd för att flytta till ett annat tillstånd. Och r är den belöning som agenten får vid det sista tidssteget genom att utföra en åtgärd för att flytta till ett annat tillstånd.

Episodiska och kontinuerliga uppgifter

Episodiska uppgifter: Vi kan säga att de har ändliga tillstånd. I till exempel tävlingsspel startar vi spelet (startar loppet) och spelar det tills spelet är slut (loppet slutar!). Detta kallas för en episod. När vi startar spelet på nytt kommer det att starta från ett starttillstånd och därför är varje episod oberoende.

Kontinuerliga uppgifter : Dessa typer av uppgifter kommer aldrig att ta slut, till exempel att lära sig koda!

Nu är det lätt att beräkna avkastningen från episodiska uppgifter eftersom de kommer att ta slut så småningom, men hur är det med kontinuerliga uppgifter, eftersom de kommer att fortsätta i all evighet. Avkastningen från summerar till oändligheten! Så hur definierar vi avkastningen för kontinuerliga uppgifter?

Det är här vi behöver Rabattfaktor (ɤ).

Rabattfaktor (ɤ): Den bestämmer hur stor vikt som ska läggas vid den omedelbara belöningen och framtida belöningar. Detta hjälper oss i princip att undvika oändlighet som belöning i kontinuerliga uppgifter. Den har ett värde mellan 0 och 1. Ett värde på 0 innebär att mer vikt läggs vid den omedelbara belöningen och ett värde på 1 innebär att mer vikt läggs vid framtida belöningar. I praktiken kommer en diskonteringsfaktor på 0 aldrig att lära sig eftersom den bara tar hänsyn till den omedelbara belöningen och en diskonteringsfaktor på 1 kommer att fortsätta med framtida belöningar, vilket kan leda till oändlighet. Det optimala värdet för diskonteringsfaktorn ligger därför mellan 0,2 och 0,8.

Så vi kan definiera avkastning med hjälp av diskonteringsfaktorn på följande sätt :(Låt oss säga att detta är ekvation 1, eftersom vi kommer att använda denna ekvation senare för att härleda Bellman-ekvationen)

Låt oss förstå det med ett exempel,Anta att du bor på en plats där det råder vattenbrist, så om någon kommer till dig och säger att han kommer att ge dig 100 liter vatten!(anta det!) under de kommande 15 timmarna som en funktion av någon parameter (ɤ).Låt oss titta på två möjligheter: (Låt oss säga att detta är ekvation 1, eftersom vi kommer att använda denna ekvation senare för att härleda Bellman-ekvationen)

En med diskonteringsfaktorn (ɤ) 0.8 :

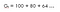
Detta innebär att vi bör vänta till den 15:e timmen eftersom minskningen inte är särskilt stor, så det är fortfarande värt att gå till slutet.Detta innebär att vi också är intresserade av framtida belöningar.Så om diskonteringsfaktorn är nära 1 kommer vi att anstränga oss för att gå till slutet eftersom belöningen är av stor betydelse.

Den andra, med diskonteringsfaktor (ɤ) 0,2 :

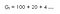
Detta innebär att vi är mer intresserade av tidiga belöningar eftersom belöningarna blir betydligt lägre för varje timme.Vi kanske inte vill vänta till slutet (till den 15:e timmen) eftersom det kommer att vara värdelöst.Om diskonteringsfaktorn är nära noll är omedelbara belöningar viktigare än framtida.

Så vilket värde på diskonteringsfaktorn ska vi använda?

Det beror på uppgiften som vi vill träna en agent för. Anta att målet i ett schackspel är att besegra motståndarens kung. Om vi lägger vikt vid de omedelbara belöningarna, t.ex. en belöning när en bonde besegrar någon av motståndarens spelare, kommer agenten att lära sig att utföra dessa delmål oavsett om hans spelare också besegras. Så i denna uppgift är framtida belöningar viktigare. I vissa fall kanske vi föredrar att använda omedelbara belöningar som i exemplet med vattnet som vi såg tidigare.

Markov Reward Process

Till dags dato har vi sett hur Markov-kedjan definierar dynamiken i en miljö med hjälp av en uppsättning tillstånd (S) och en matris för sannolikheten för övergångar (P), men vi vet att förstärkningsinlärning handlar om att maximera belöningen, så vi lägger till belöning till Markov-kedjan, vilket ger oss Markov Reward Process.

Markov Reward Process : Som namnet antyder är MDP:er Markovkedjor med värdebedömning.I grund och botten får vi ett värde från varje tillstånd som vår agent befinner sig i.

Matematiskt definierar vi Markov Reward Process som :

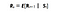
Vad den här ekvationen betyder är hur mycket belöning (Rs) vi får från ett visst tillstånd S. Detta talar om den omedelbara belöningen från just det tillståndet som vår agent är i. Som vi kommer att se i nästa berättelse hur vi maximerar dessa belöningar från varje tillstånd som vår agent befinner sig i. Enkelt uttryckt maximerar vi den kumulativa belöningen vi får från varje tillstånd.

Vi definierar MRP som (S,P,R,ɤ) ,där :

• S är en uppsättning tillstånd,
• P är övergångssannolikhetsmatrisen,
• R är belöningsfunktionen , som vi såg tidigare,
• ɤ är diskonteringsfaktorn

Markov beslutsprocess

Nu ska vi utveckla vår intuition för Bellmanekvationen och Markov beslutsprocessen.

Policyfunktion och värdefunktion

Värdefunktionen bestämmer hur bra det är för agenten att befinna sig i ett visst tillstånd. För att bestämma hur bra det är att befinna sig i ett visst tillstånd måste det naturligtvis bero på vissa åtgärder som den kommer att vidta. Det är här politiken kommer in i bilden. En policy definierar vilka åtgärder som ska utföras i ett visst tillstånd s.

En policy är en enkel funktion, som definierar en sannolikhetsfördelning över åtgärder (a∈ A) för varje tillstånd (s ∈ S). Om en agent vid tid t följer en policy π är π(a|s) sannolikheten för att agenten med att vidta åtgärden (a ) vid ett visst tidssteg (t) I Reinforcement Learning bestämmer agentens erfarenhet förändringen av policyn. Matematiskt definieras en policy på följande sätt :

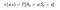
Nu, hur hittar vi ett värde för ett tillstånd.Värdet av tillstånd s, när agenten följer en policy π som betecknas med vπ(s), är den förväntade avkastningen med utgångspunkt i s och med en policy π för de kommande tillstånden, tills vi når det slutliga tillståndet.Vi kan formulera detta som: (Denna funktion kallas också för State-value Function)

Denna ekvation ger oss den förväntade avkastningen som utgår från tillstånd(s) och som går till efterföljande tillstånd därefter, med politiken π. En sak att notera är att den avkastning vi får är stokastisk medan värdet av en stat inte är stokastiskt. Det är den förväntade avkastningen från starttillstånd s och därefter till alla andra tillstånd. Observera också att värdet av sluttillståndet (om det finns något) är noll. Låt oss titta på ett exempel :

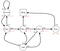
Antag att vårt starttillstånd är klass 2, och att vi flyttar oss till klass 3 och sedan passerar vi till klass 3 och sedan till sömn.kort sagt, klass 2 > klass 3 > pass > sömn.

Vår förväntade avkastning är med diskonteringsfaktor 0,5:

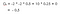
Notera: Det är -2 + (-2 * 0.5) + 10 * 0.25 + 0 istället för -2 * -2 * -2 * 0.5 + 10 * 0.25 + 0.Då är värdet av klass 2 -0.5 .

Bellmanekvation för värdefunktion

Bellmanekvationen hjälper oss att hitta optimal politik och värdefunktion.Vi vet att vår politik förändras med erfarenheten, så vi kommer att ha olika värdefunktion i enlighet med olika politik.Optimal värdefunktion är den som ger maximalt värde jämfört med alla andra värdefunktioner.

Bellmanekvationen anger att värdefunktionen kan delas in i två delar:

Omedelbar belöning, R

Diskonterat värde av efterföljande tillstånd,

Matematiskt kan vi definiera Bellmanekvationen som :

Låt oss förstå vad denna ekvation säger med hjälp av ett exempel :

Förutsatt att en robot befinner sig i ett visst tillstånd (s) och sedan förflyttar sig från detta tillstånd till ett annat tillstånd (s’). Nu är frågan hur bra det var för roboten att befinna sig i tillståndet (s). Med hjälp av Bellmans ekvation kan vi säga att det är den förväntade belöningen som roboten fick när den lämnade tillståndet (s) plus värdet av det tillstånd (s’) som den flyttade till.

Låt oss titta på ett annat exempel :

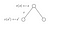
Vi vill veta värdet av tillstånd s.Värdet av tillstånd s är den belöning vi fick när vi lämnade det tillståndet plus det diskonterade värdet av det tillstånd vi hamnade i multiplicerat med övergångssannolikheten att vi kommer att flytta in i det.

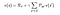
Ovanstående ekvation kan uttryckas i matrisform enligt följande :

Varvid v är värdet av det tillstånd vi befann oss i, vilket är lika med den omedelbara belöningen plus det diskonterade värdet av nästa tillstånd multiplicerat med sannolikheten att gå in i detta tillstånd.

Den löpande tidskomplexiteten för denna beräkning är O(n³). Därför är detta helt klart inte en praktisk lösning för att lösa större MRP:er (detsamma gäller för MDP:er).I senare bloggar kommer vi att titta på effektivare metoder som dynamisk programmering (värdeiteration och policyiteration), Monte-Claro-metoder och TD-Learning.

Vi kommer att prata om Bellmanekvationen i mycket större detalj i nästa berättelse.

Vad är Markov Decision Process?

Markov Decision Process : Det är Markov Reward Process med ett beslut.Allt är likadant som i MRP, men nu har vi ett verkligt organ som fattar beslut eller vidtar åtgärder.

Det är en tupel av (S, A, P, R, 𝛾) där:

• S är en uppsättning tillstånd,
• A är uppsättningen åtgärder som agenten kan välja att vidta,
• P är övergångssannolikhetsmatrisen,
• R är belöningen som ackumulerats genom agentens åtgärder,
• 𝛾 är diskonteringsfaktorn.

P och R kommer att förändras något med hänsyn till handlingarna enligt följande :

Transition Probability Matrix

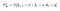
Belöningsfunktion

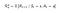
Nu är vår belöningsfunktion beroende av handlingen.

Till dags dato har vi talat om att få en belöning (r) när vår agent går igenom en uppsättning tillstånd (s) och följer en policy π.I Markov Decision Process (MDP) är policyn faktiskt mekanismen för att fatta beslut.Så nu har vi en mekanism som väljer att vidta en åtgärd.

Policyn i en MDP är beroende av det aktuella tillståndet.Den är inte beroende av historiken.Det är Markov-egenskapen.Så det aktuella tillståndet som vi befinner oss i karaktäriserar historiken.

Vi har redan sett hur bra det är för agenten att befinna sig i ett visst tillstånd(Tillståndsvärdesfunktion).Låt oss nu se hur bra det är att vidta en viss åtgärd enligt en policy π från tillstånd s (Åtgärdsvärdesfunktion).

Åtgärdsvärdesfunktion för tillstånd-åtgärd eller Q-funktion

Denna funktion specificerar hur bra det är för agenten att vidta åtgärden (a) i ett tillstånd (s) med en policy π.

Matematiskt kan vi definiera State-action value function som :

Basiskt sett talar den om hur värdefullt det är att utföra en viss handling (a) i ett tillstånd (s) med en policy π.

Låt oss titta på ett exempel på Markov Decision Process :

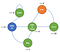
Nu kan vi se att det inte finns några fler sannolikheter.Nu har vår agent faktiskt val att göra, t.ex. efter att ha vaknat kan vi välja att titta på Netflix eller koda och felsöka.Naturligtvis är agentens handlingar definierade utifrån en viss policy π och kommer att belönas i enlighet med detta.