Ett elektromagnetiskt metamaterial påverkar elektromagnetiska vågor som träffar eller interagerar med dess strukturella egenskaper som är mindre än våglängden. För att bete sig som ett homogent material som exakt beskrivs av ett effektivt brytningsindex måste dess egenskaper vara mycket mindre än våglängden.
För mikrovågsstrålning är egenskaperna i storleksordningen millimeter. Metamaterial för mikrovågsfrekvens är vanligtvis konstruerade som matriser av elektriskt ledande element (t.ex. trådslingor) som har lämpliga induktiva och kapacitiva egenskaper. Många mikrovågsmetamaterial använder delade ringresonatorer.
Fotoniska metamaterial är strukturerade på nanometerskala och manipulerar ljus vid optiska frekvenser. Fotoniska kristaller och frekvensselektiva ytor såsom diffraktionsgitter, dielektriska speglar och optiska beläggningar uppvisar likheter med strukturerade metamaterial under våglängden. Dessa anses dock vanligtvis skilja sig från metamaterial, eftersom deras funktion beror på diffraktion eller interferens och därför inte kan approximeras som ett homogent material. Materialstrukturer som fotoniska kristaller är dock effektiva inom det synliga ljusspektrumet. Den mellersta delen av det synliga spektrumet har en våglängd på cirka 560 nm (för solljus). Fotografiska kristallstrukturer är i allmänhet hälften så stora eller mindre, det vill säga <280 nm.
Plasmoniska metamaterial utnyttjar ytplasmoner, som är paket av elektrisk laddning som kollektivt oscillerar vid metallytor vid optiska frekvenser.
Frekvensselektiva ytor (FSS) kan uppvisa egenskaper som är mindre än en våglängd och kallas på olika sätt artificiella magnetiska ledare (AMC) eller högimpedansytor (HIS). FSS uppvisar induktiva och kapacitiva egenskaper som är direkt relaterade till deras struktur under våglängden.
Elektromagnetiska metamaterial kan delas in i olika klasser enligt följande:
Negativt brytningsindexEdit
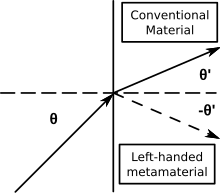
Metamaterial med negativt index (NIM) kännetecknas av ett negativt brytningsindex. Andra termer för NIM är bland annat ”vänsterhänt media”, ”media med negativt brytningsindex” och ”backward-wave media”. NIM där det negativa brytningsindexet härrör från samtidigt negativ permittivitet och negativ permeabilitet kallas också dubbelnegativa metamaterial eller dubbelnegativa material (DNG).
Att anta ett material som är väl tillnärmat genom en verklig permittivitet och permeabilitet, är förhållandet mellan permittivitet ϵ r {\displaystyle \epsilon _{r}}

, permeabilitet μ r {\displaystyle \mu _{r}}

och brytningsindex n ges av n = ± ϵ r μ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{\mathrm {r} }\mu _{\mathrm {r} }}}}

. Alla kända transparenta icke-metamaterialmaterial (glas, vatten, …) har positiva ϵ r {\displaystyle \epsilon _{r}}

och μ r {\displaystyle \mu _{r}}

. Konventionellt används den positiva kvadratroten för n. Vissa konstruerade metamaterial har dock ϵ r {\displaystyle \epsilon _{r}}

och μ r < 0 {\displaystyle \mu _{r}<0}

. Eftersom produkten ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}}

är positiv, är n verklig. Under sådana omständigheter är det nödvändigt att ta den negativa kvadratroten för n. När både ϵ r {\displaystyle \epsilon _{r}}

och μ r {\displaystyle \mu _{r}}

är positiva (negativa), rör sig vågorna i riktning framåt (bakåt). Elektromagnetiska vågor kan inte utbreda sig i material med ϵ r {\displaystyle \epsilon _{r}}

och μ r {\displaystyle \mu _{r}}

med motsatt tecken när brytningsindexet blir imaginärt. Sådana material är ogenomskinliga för elektromagnetisk strålning och exempel är plasmoniska material som metaller (guld, silver, …).
De ovanstående övervägandena är förenklade för verkliga material, som måste ha komplexa värden ϵ r {\displaystyle \epsilon _{r}}.

och μ r {\displaystyle \mu _{r}}

. Realdelarna av både ϵ r {\displaystyle \epsilon _{r}}

och μ r {\displaystyle \mu _{r}}

behöver inte vara negativa för att ett passivt material ska uppvisa negativ refraktion. Ett negativt brytningsindex för cirkulärt polariserade vågor kan faktiskt också uppstå på grund av kiralitet. Metamaterial med negativt n har många intressanta egenskaper:
- Snells lag (n1sinθ1 = n2sinθ2) beskriver fortfarande brytning, men eftersom n2 är negativt är infallande och brytande strålar på samma sida av ytnormalen vid ett gränssnitt av material med positivt och negativt index.
- Cherenkovstrålning pekar åt andra hållet.
- Den tidsmedelvärdeberäknade Poyntingvektorn är antiparallell till fashastigheten. För att vågor (energi) ska kunna fortplanta sig måste dock en -µ paras med en -ε för att uppfylla vågtalets beroende av materialparametrarna k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }}}
.
Negativt brytningsindex härrör matematiskt från vektortripletten E, H och k.
För plana vågor som utbreder sig i elektromagnetiska metamaterial följer det elektriska fältet, det magnetiska fältet och vågevektorn en vänsterhängesregel, vilket är det motsatta till beteendet hos konventionella optiska material.
Hittills är det bara metamaterial som uppvisar ett negativt brytningsindex.
Enkel negativEdit
Enkla negativa (SNG) metamaterial har antingen negativ relativ permittivitet (εr) eller negativ relativ permeabilitet (µr), men inte båda. De fungerar som metamaterial när de kombineras med en annan, kompletterande SNG, som tillsammans fungerar som en DNG.
Epsilonnegativa medier (ENG) har en negativ εr medan µr är positiv. Många plasmor uppvisar denna egenskap. Till exempel är ädelmetaller som guld eller silver ENG i det infraröda och synliga spektrumet.
Mu-negativa medier (MNG) uppvisar ett positivt εr och ett negativt µr. Gyrotropiska eller gyromagnetiska material uppvisar denna egenskap. Ett gyrotropiskt material är ett material som har förändrats av närvaron av ett kvasistatiskt magnetfält, vilket möjliggör en magnetoptisk effekt. En magnetoptisk effekt är ett fenomen där en elektromagnetisk våg fortplantar sig genom ett sådant medium. I ett sådant material kan vänster- och högerroterande elliptiska polarisationer fortplanta sig med olika hastigheter. När ljus överförs genom ett lager av magneto-optiskt material kallas resultatet för Faraday-effekten: polarisationsplanet kan roteras, vilket bildar en Faraday-roterare. Resultatet av en sådan reflektion kallas den magnetoptiska Kerr-effekten (inte att förväxla med den icke-linjära Kerr-effekten). Två gyrotropa material med omvända rotationsriktningar för de två huvudpolarisationerna kallas optiska isomerer.
Att sammanfoga en platta av ENG-material och en platta av MNG-material resulterade i egenskaper som resonanser, anomal tunnling, transparens och nollreflektion. I likhet med material med negativt index är SNG:erna naturligt dispersiva, så deras εr, µr och brytningsindex n, är en funktion av frekvensen.
HyperbolicEdit
Hyperboliska metamaterial (HMM:er) beter sig som en metall för en viss polarisering eller riktning av ljusets utbredning och beter sig som ett dielektrikum för den andra på grund av de negativa och positiva permittivitetstensorkomponenterna, vilket ger en extrem anisotropi. Materialets spridningsrelation i vågvektorrummet bildar en hyperboloid och därför kallas det ett hyperboliskt metamaterial. Den extrema anisotropin hos HMM leder till riktad ljusutbredning inom och på ytan. HMM har visat olika potentiella tillämpningar, t.ex. avkänning, avbildning, styrning av optiska signaler och förstärkta plasmonresonanseffekter.
BandgapEdit
Elektromagnetiska metamaterial med bandgap (EBG eller EBM) kontrollerar ljusets utbredning. Detta sker antingen med fotoniska kristaller (PC) eller vänsterhänta material (LHM). PC kan förbjuda ljusutbredning helt och hållet. Båda klasserna kan tillåta att ljuset fortplantar sig i specifika, utformade riktningar och båda kan utformas med bandgap vid önskade frekvenser. EBG:s periodstorlek är en betydande del av våglängden, vilket skapar konstruktiv och destruktiv interferens.
PC skiljer sig från strukturer under våglängden, t.ex. avstämbara metamaterial, eftersom PC:s egenskaper härrör från dess bandgapegenskaper. PC är dimensionerade för att matcha ljusets våglängd, i motsats till andra metamaterial som exponerar subvåglängdsstrukturer. Dessutom fungerar PC genom att diffraktera ljus. Metamaterial använder däremot inte diffraktion.
PC:er har periodiska inneslutningar som hämmar vågutbredningen på grund av inneslutningarnas destruktiva interferens från spridning. PC:s fotoniska bandgapegenskap gör dem till en elektromagnetisk analog till elektroniska halvledarkristaller.
EBG:er har som mål att skapa periodiska dielektriska strukturer med hög kvalitet och låga förluster. En EBG påverkar fotoner på samma sätt som halvledarmaterial påverkar elektroner. PC är det perfekta bandgapmaterialet, eftersom de inte tillåter någon ljusutbredning. Varje enhet i den föreskrivna periodiska strukturen fungerar som en atom, om än av mycket större storlek.
EBGs är utformade för att förhindra utbredning av en tilldelad bandbredd av frekvenser, för vissa ankomstvinklar och polarisationer. Olika geometrier och strukturer har föreslagits för att framställa EBG:s speciella egenskaper. I praktiken är det omöjligt att bygga en felfri EBG-enhet.
EBG:er har tillverkats för frekvenser som sträcker sig från några gigahertz (GHz) till några terahertz (THz), radio-, mikrovågs- och medelinfraröda frekvensområden. EBG-tillämpningar omfattar en transmissionsledning, träpålar tillverkade av fyrkantiga dielektriska stavar och flera olika typer av antenner med låg förstärkning.
Dubbelpositivt mediumRedigera
Dubbelpositiva medier (DPS) förekommer i naturen, t.ex. naturligt förekommande dielektriska material. Permittiviteten och den magnetiska permeabiliteten är båda positiva och vågutbredningen sker i framåtriktad riktning. Konstgjorda material har tillverkats som kombinerar DPS-, ENG- och MNG-egenskaper.
Bi-isotropa och bianisotropaRedigera
Kategoriseringen av metamaterial i dubbel- eller enkelnegativa, eller dubbelpositiva, utgår normalt från att metamaterialet har oberoende elektriska och magnetiska reaktioner som beskrivs av ε och µ. I många fall orsakar dock det elektriska fältet magnetisk polarisering, medan det magnetiska fältet inducerar elektrisk polarisering, känd som magnetoelektrisk koppling. Sådana medier betecknas som bi-isotropa. Medier som uppvisar magnetoelektrisk koppling och som är anisotropa (vilket är fallet för många metamaterialstrukturer) kallas bi-anisotropa.
Fyra materialparametrar är inneboende för magnetoelektrisk koppling av bi-isotropa medier. De är de elektriska (E) och magnetiska (H) fältstyrkorna samt de elektriska (D) och magnetiska (B) flödestätheterna. Dessa parametrar är ε, µ, κ och χ eller permittivitet, permeabilitet, kiralitetsstyrka respektive Tellegenparametern. I denna typ av medier varierar inte materialparametrarna med förändringar längs ett roterat koordinatsystem för mätningar. I denna mening är de invarianta eller skalära.
De inneboende magnetoelektriska parametrarna, κ och χ, påverkar vågens fas. Kiralitetsparameterns effekt är att brytningsindexet delas upp. I isotropa medier resulterar detta i vågutbredning endast om ε och µ har samma tecken. I bi-isotropa medier där χ antas vara noll och κ har ett värde som inte är noll, uppstår andra resultat. Antingen kan en bakåtriktad våg eller en framåtriktad våg uppstå. Alternativt kan två framåtriktade vågor eller två bakåtriktade vågor uppstå, beroende på styrkan hos chiralitetsparametern.
I det allmänna fallet lyder de konstitutiva relationerna för bi-anisotropa material D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}

där ϵ {\displaystyle \epsilon }

och μ {\displaystyle \mu }

är permittiviteten respektive permeabiliteten, medan ξ {\displaystyle \xi }

och ζ {\displaystyle \zeta }

är de två magneto-elektriska tensorerna. Om mediet är reciprokt är permittivitet och permeabilitet symmetriska tensorer, och ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}

, där κ {\displaystyle \kappa }

är den chirala tensorn som beskriver den chirala elektromagnetiska och reciproka magneto-elektriska responsen. Den kirala sensorn kan uttryckas som κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}}\operatorname {tr} (\kappa )I+N+J}}

, där tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

är spåret av κ {\displaystyle \kappa }

, I är identitetsmatrisen, N är en symmetrisk spårfri tensor och J är en antisymmetrisk tensor. En sådan dekomposition gör det möjligt att klassificera den reciproka bianisotropa responsen och vi kan identifiera följande tre huvudklasser: (i) kirala medier ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}

), (ii) pseudokirala medier ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )=0,N\neq 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}

).
ChiralEdit
Metamaterialens handsidighet är en potentiell källa till förvirring eftersom metamateriallitteraturen innehåller två motstridiga användningar av termerna vänster- och högerhänt. Den första hänvisar till en av de två cirkulärt polariserade vågor som är utbredningsformerna i chirala medier. Den andra avser den trippel av elektriskt fält, magnetiskt fält och Poyntingvektor som uppstår i medier med negativt brytningsindex, som i de flesta fall inte är kirala.
Generellt sett är ett kiralt och/eller bianisotropt elektromagnetiskt svar en följd av 3D-geometrisk kiralitet: 3D-kirala metamaterial är sammansatta genom inbäddning av 3D-kirala strukturer i ett värdmedium och de uppvisar kiralitetsrelaterade polariseringseffekter, som optisk aktivitet och cirkulär dikroism. Begreppet 2D-kiralitet finns också och ett plant objekt sägs vara kiralt om det inte kan överlagras med sin spegelbild om det inte lyfts ur planet. 2D-kirala metamaterial som är anisotropa och förlustbringande har observerats uppvisa riktningsasymmetrisk överföring (reflektion, absorption) av cirkulärt polariserade vågor på grund av cirkulär konverteringsdichrosim. Å andra sidan kan bianisotropisk respons uppstå från geometriska achirala strukturer som varken har 2D- eller 3D-egentlig kiralitet. Plum och medarbetare undersökte magneto-elektrisk koppling på grund av extrinsisk kiralitet, där arrangemanget av en (achiral) struktur tillsammans med strålningsvågvektorn skiljer sig från dess spegelbild, och observerade stor, avstämbar linjär optisk aktivitet, icke-linjär optisk aktivitet, speglande optisk aktivitet och cirkulär konverteringsdichroism. Rizza et al. föreslog 1D-kirala metamaterial där den effektiva kirala tensorn inte är försvinnande om systemet är geometriskt endimensionellt kiralt (spegelbilden av hela strukturen kan inte överlagras på den med hjälp av translationer utan rotationer).
3D-kirala metamaterial konstrueras av kirala material eller resonatorer där den effektiva kiralitets parametern κ {\displaystyle \kappa }

inte är noll. Vågutbredningsegenskaper i sådana kirala metamaterial visar att negativ brytning kan realiseras i metamaterial med stark kiralitet och positiv ϵ r {\displaystyle \epsilon _{r}}

och μ r {\displaystyle \mu _{r}}

. Detta beror på att brytningsindexet n {\displaystyle n}

har olika värden för vänster och höger cirkulärt polariserade vågor, vilket ges av
n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}}\pm \kappa }

Det kan konstateras att ett negativt index kommer att uppträda för en polarisering om κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}

. I detta fall är det inte nödvändigt att någon av eller båda ϵ r {\displaystyle \epsilon _{r}}

och μ r {\displaystyle \mu _{r}}

vara negativa för vågutbredning bakåt. Ett negativt brytningsindex på grund av kiralitet observerades först samtidigt och oberoende av varandra av Plum et al. och Zhang et al. 2009.
FSS basedEdit
Frekvensselektiva ytbaserade metamaterial blockerar signaler i ett vågband och släpper igenom dem vid ett annat vågband. De har blivit ett alternativ till metamaterial med fast frekvens. De möjliggör valfria förändringar av frekvenser i ett enda medium, i stället för de restriktiva begränsningar som ett fast frekvenssvar innebär.
