I handledningen om generaliserade linjära modeller lärde vi oss om olika GLM:er som linjär regression, logistisk regression etc.. I den här handledningen i TechVidvans R-handledningsserie kommer vi att titta på linjär regression i R i detalj. Vi kommer att lära oss vad linjär regression i R är och hur man implementerar den i R. Vi kommer att titta på skattningsmetoden minsta kvadrat och kommer också att lära oss hur man kontrollerar modellens noggrannhet.

Så, utan vidare, låt oss komma igång!

Linjär regression i R

Linjär regression i R är en metod som används för att förutsäga värdet av en variabel med hjälp av värdet eller värdena av en eller flera indata prediktorvariabler. Målet med linjär regression är att upprätta ett linjärt samband mellan den önskade utfallsvariabeln och de ingående prediktorerna.

För att modellera en kontinuerlig variabel Y som en funktion av en eller flera ingående prediktorvariabler Xi, så att funktionen kan användas för att förutsäga värdet av Y när endast värdena av Xi är kända. Den allmänna formen för ett sådant linjärt förhållande är:

Y=?0+?1 X

Här är ?0 interceptet
och ?1 lutningen.

Typer av linjär regression i R

Det finns två typer av linjär regression i R:

• Enkla linjära regressioner
• Multipla linjära regressioner

Låts oss titta på dessa en och en.

Enklare linjär regression i R

Enklare linjär regression syftar till att hitta ett linjärt samband mellan två kontinuerliga variabler. Det är viktigt att notera att förhållandet är statistiskt till sin natur och inte deterministiskt.

Ett deterministiskt förhållande är ett förhållande där värdet av en variabel kan hittas exakt genom att använda värdet av den andra variabeln. Ett exempel på ett deterministiskt förhållande är det mellan kilometer och miles. Genom att använda kilometervärdet kan vi exakt hitta avståndet i miles. Ett statistiskt förhållande är inte exakt och har alltid ett förutsägelsefel. Med tillräckligt med data kan vi till exempel hitta ett samband mellan en persons längd och vikt, men det kommer alltid att finnas en felmarginal och det kommer att finnas undantagsfall.

Tanken bakom enkel linjär regression är att hitta en linje som passar bäst till de givna värdena för båda variablerna. Denna linje kan sedan hjälpa oss att hitta värdena för den beroende variabeln när de saknas.

Låt oss studera detta med hjälp av ett exempel. Vi har ett dataset som består av höjder och vikter för 500 personer. Vårt mål här är att bygga en linjär regressionsmodell som formulerar förhållandet mellan längd och vikt, så att när vi ger höjd(Y) som indata till modellen kan den ge vikt(X) tillbaka till oss med minsta möjliga felmarginal.

Y=b0+b1X

Värdena för b0 och b1 bör väljas så att de minimerar felmarginalen. Felmåttet kan användas för att mäta modellens noggrannhet.

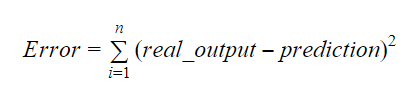
Vi kan beräkna lutningen eller koefficienten på följande sätt: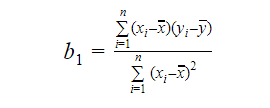

Värdet på b1 ger oss en inblick i arten av förhållandet mellan de beroende och de oberoende variablerna.

• Om b1 > 0 har variablerna ett positivt samband dvs. en ökning av x leder till en ökning av y.
• Om b1 < 0 har variablerna ett negativt förhållande, dvs. en ökning av x leder till en minskning av y.

Värdet av b0 eller interceptet kan beräknas på följande sätt: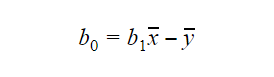
Värdet av b0 kan också ge mycket information om modellen och vice versa.

Om modellen inte inkluderar x=0 är förutsägelsen meningslös utan b1. För att modellen endast ska ha b0 och inte b1 i sig vid någon punkt måste värdet på x vara 0 vid den punkten. I fall som höjd kan x inte vara 0 och en persons höjd kan inte vara 0. Därför är en sådan modell meningslös med endast b0.

Om termen b0 saknas kommer modellen att passera genom ursprunget, vilket innebär att förutsägelsen och regressionskoefficienten (lutningen) kommer att vara snedvriden.

Multipel linjär regression i R

Multipel linjär regression är en utvidgning av enkel linjär regression. I multipel linjär regression strävar vi efter att skapa en linjär modell som kan förutsäga värdet av målvariabeln med hjälp av värdena för flera prediktorvariabler. Den allmänna formen för en sådan funktion är följande:

Y=b0+b1X1+b2X2+…+bnXn

Bedömning av modellens noggrannhet

Det finns olika metoder för att bedöma modellens kvalitet och noggrannhet. Låt oss ta en titt på några av dessa metoder en i taget.

R-kvadrat

Den verkliga informationen i data är den varians som förmedlas i dem. R-kvadrat talar om hur stor andel av variationen i målvariabeln (y) som förklaras av modellen. Vi kan hitta R-kvadratmåttet för en modell med hjälp av följande formel: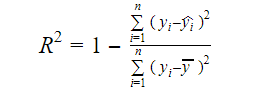

Varvid,

• yi är det inpassade värdet av y för observation i
• y är medelvärdet av Y.

Ett lägre värde på R-kvadrat innebär en lägre noggrannhet hos modellen. R-kvadratmåttet är dock inte nödvändigtvis en slutgiltig avgörande faktor.

Adjusterat R-kvadrat

När antalet variabler i modellen ökar, ökar också R-kvadratvärdet. Detta orsakar också fel i den variation som förklaras av de nytillkomna variablerna. Därför justerar vi formeln för R-kvadrat för flera variabler.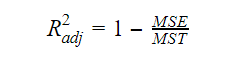
Här står MSE för Mean Standard Error vilket är:

Och MST står för Mean Standard Total vilket ges av: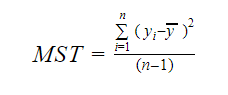

Varvid, n är antalet observationer och q är antalet koefficienter.

Sambandet mellan R-kvadrat och justerat R-kvadrat är: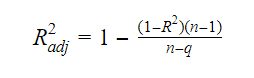

Standardfel och F-statistik

Standardfelet och F-statistiken är båda mått på kvaliteten på anpassningen av en modell. Formlerna för standardfel och F-statistik är:

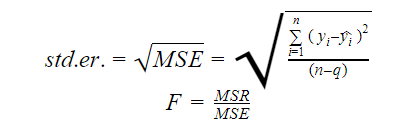
Varvid MSR står för Mean Square Regression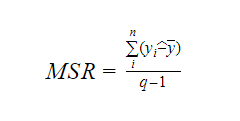

AIC och BIC

Akaikes informationskriterie och Bayesianskt informationskriterie är mått på kvaliteten på anpassningen av statistiska modeller. De kan också användas som kriterier för val av modell.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Varvid,

• L är likelihood-funktionen,
• k är antalet modellparametrar,
• n är urvalets storlek.

lm-funktionen i R

Funktionen lm() i R anpassar linjära modeller. Den kan utföra regression och analys av varians och kovarians. Syntaxen för funktionen lm är följande:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Varför,

• formula är ett objekt av klassen ”formula” och är en symbolisk representation av den modell som ska anpassas,
• data är dataramen eller listan som innehåller variablerna i formeln(data är ett valfritt argument. Om det saknas hämtar funktionen variablerna från miljön),
• subset är en valfri vektor som innehåller en delmängd observationer som ska användas i anpassningen,
• weights är en valfri vektor som anger de vikter som ska användas i anpassningen,
• na.action är en funktion som visar vad som ska hända när NA förekommer i data,
• method anger metoden för anpassning av modellen,
• model, x, y och qr är logiska värden som styr om motsvarande värden ska returneras med resultatet eller inte. Dessa värden är:
• model: modellramen
• x: modellmatrisen
• y: svaret
• qr: qr-dekompositionen
• singular.ok är en logisk som kontrollerar om singulära anpassningar tillåts eller inte,
• offset är en i förväg känd prediktor som ska användas i modellen,
• . . . är ytterligare argument som ska skickas till regressionsfunktioner på lägre nivå.

Praktiskt exempel på linjär regression i R

Det räcker med teori för tillfället. Låt oss ta en titt på hur man implementerar allt detta. Vi ska anpassa en linjär modell med hjälp av linjär regression i R med hjälp av funktionen lm(). Vi kommer också att kontrollera modellens passningskvalitet efteråt. Låt oss använda datasetet cars som tillhandahålls som standard i baspaketet R.

1. Låt oss börja med en grafisk analys av datasetet för att bli mer bekanta med det. För att göra det kommer vi att rita en spridningsdiagram och kontrollera vad det säger oss om data.

Vi kan använda funktionen scatter.smooth() för att skapa ett spridningsdiagram för datasetet.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Output

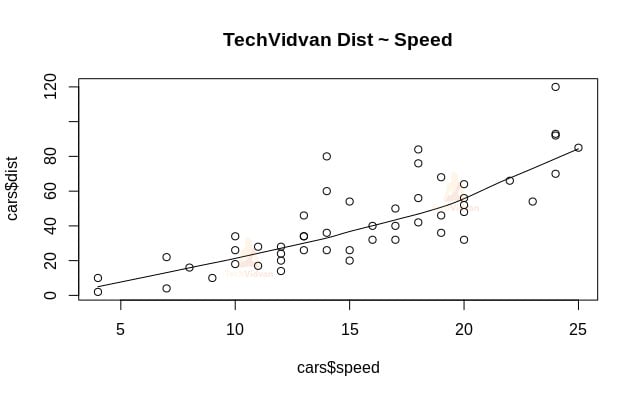
Spridningsdiagrammet visar oss en positiv korrelation mellan avstånd och hastighet. Det tyder på ett linjärt ökande samband mellan de två variablerna. Detta gör att data lämpar sig för linjär regression eftersom ett linjärt samband är ett grundläggande antagande för att anpassa en linjär modell till data.

2. Nu när vi har verifierat att linjär regression lämpar sig för data kan vi använda funktionen lm() för att anpassa en linjär modell till dem.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Utmatning

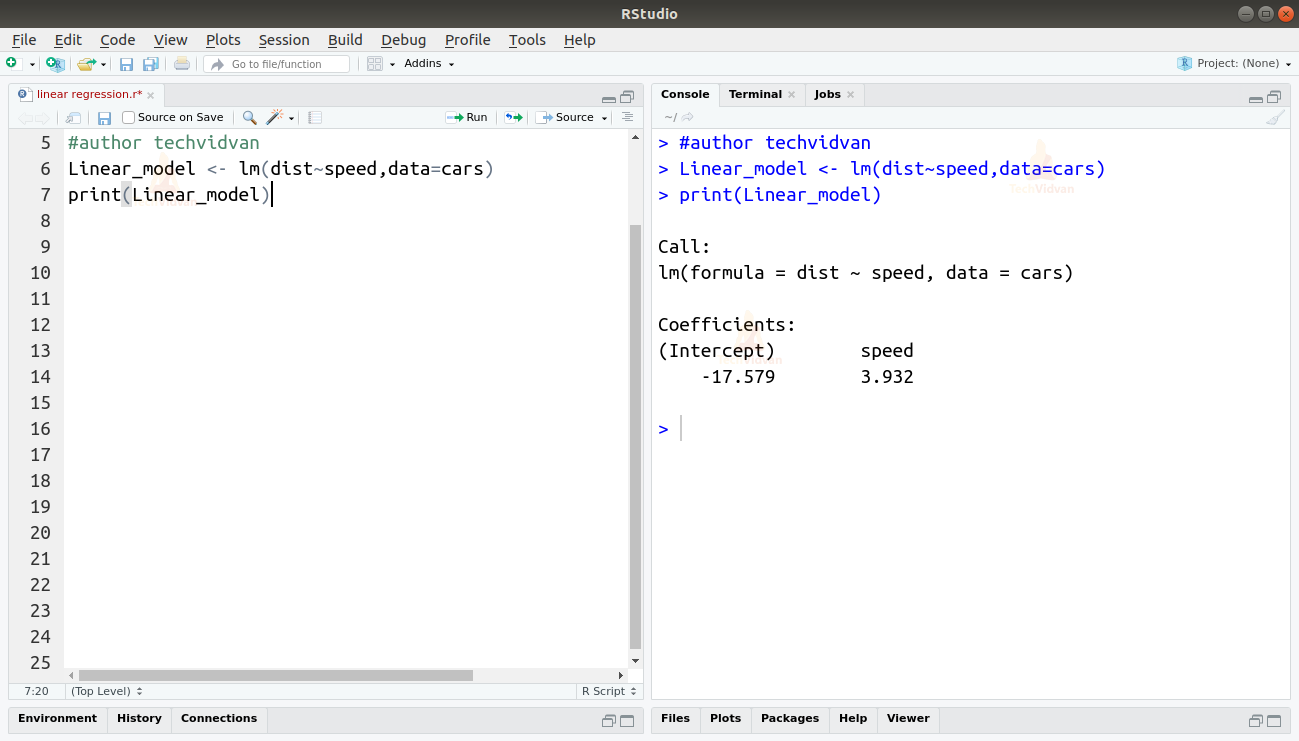
Utmatningen från funktionen lm() visar oss interceptet och hastighetskoefficienten. Därmed definieras det linjära sambandet mellan avstånd och hastighet som:

Distans=Intercept+koefficient*hastighet

Distans=-17,579+3,932*hastighet

3. Nu när vi har anpassat en modell ska vi kontrollera kvaliteten eller lämpligheten av anpassningen. Vi börjar med att kontrollera sammanfattningen av den linjära modellen med hjälp av funktionen summary().

summary(Linear_model)

Output

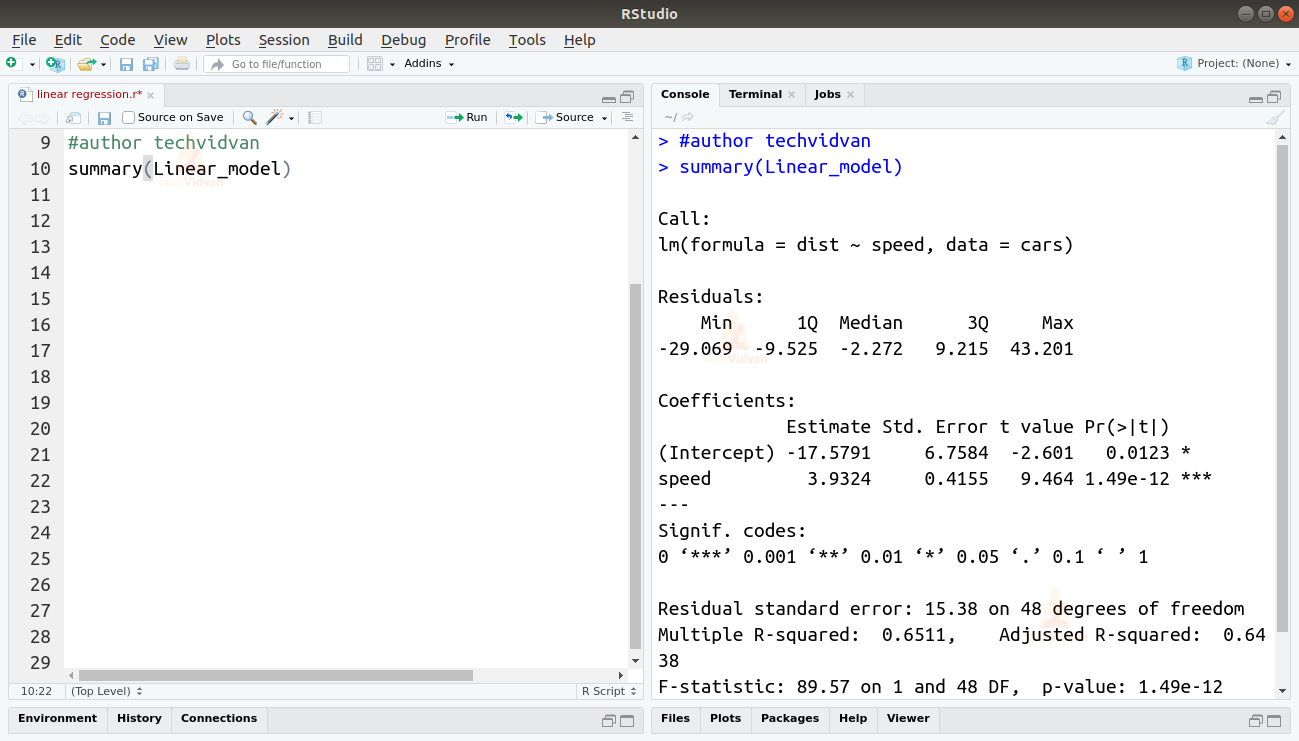
Funktionen summary() ger oss några viktiga mått som hjälper oss att diagnostisera modellens anpassning. P-värdet är ett viktigt mått på hur passande en modell är. En modell anses inte passa om p-värdet är högre än en förutbestämd statistisk signifikansnivå som idealt sett är 0,05.

Sammanfattningen ger oss också t-värdet. Ju högre t-värde desto bättre passar modellen.
Vi kan också hitta AIC och BIC genom att använda funktionerna AIC() och BIC().

AIC(Linear_model)BIC(Linear_model)

Output

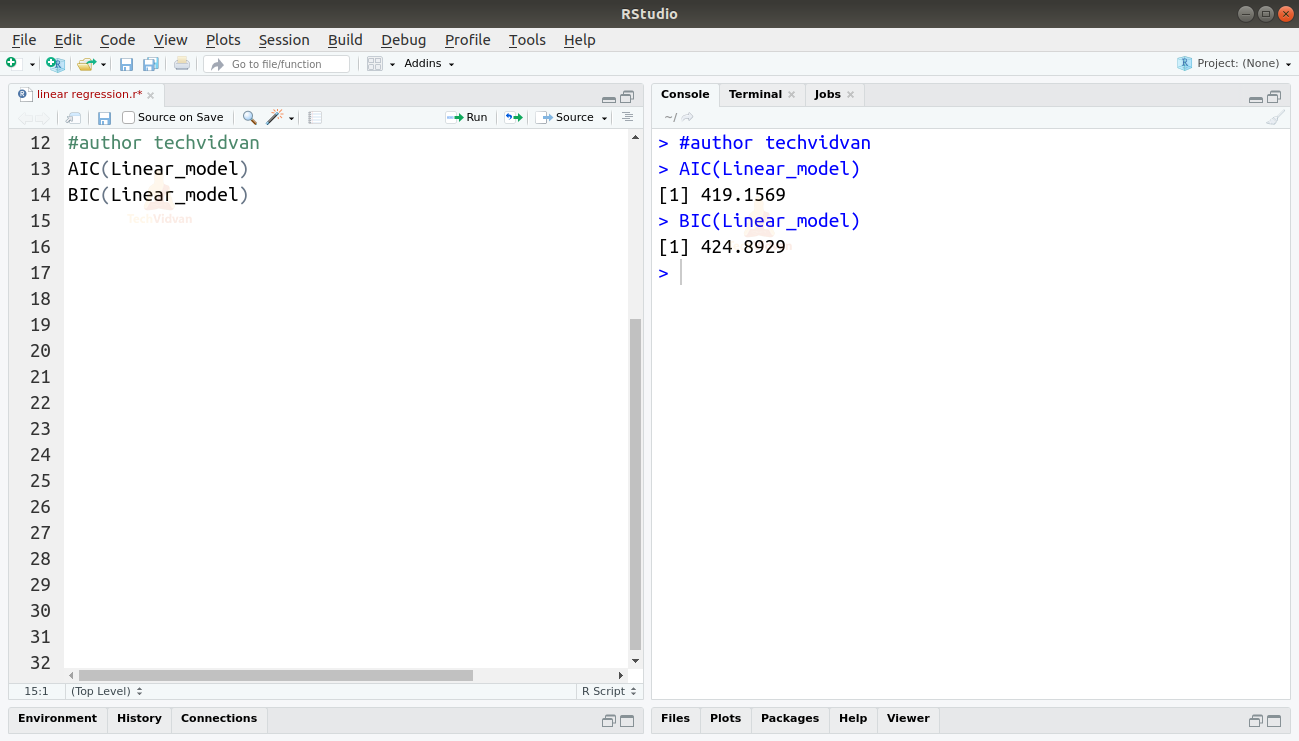
Den modell som resulterar i de lägsta AIC- och BIC-värdena är den mest föredragna.

Sammanfattning

I det här kapitlet i TechVidvans R-tutorialserie lärde vi oss om linjär regression. Vi lärde oss om enkel linjär regression och multipel linjär regression. Sedan studerade vi olika mått för att bedöma modellens kvalitet eller noggrannhet, som R2, justerad R2, standardfel, F-statistik, AIC och BIC. Vi lärde oss sedan hur man implementerar linjär regression i R. Vi kontrollerade sedan kvaliteten på modellens anpassning i R.

Dela gärna ditt betyg på Google om du gillade handledningen om linjär regression.