Hej gott folk! I den här artikeln kommer jag att beskriva en algoritm som används inom Natural Language Processing: Latent Semantic Analysis ( LSA ).
De viktigaste tillämpningarna av denna ovan nämnda metod är omfattande inom lingvistiken: Den här metoden är mycket omfattande: Jämförelse av dokument i lågdimensionella utrymmen (dokumentlikhet), hitta återkommande ämnen i dokumenten (ämnesmodellering), hitta relationer mellan termer (textsynonymitet).

Introduktion
Modellen för latent semantisk analys är en teori om hur betydelser
representationer kan läras in genom att man möter stora språkprov utan explicita anvisningar om hur språket är strukturerat.
Problemet vid handen är inte övervakat, det vill säga vi har inga fasta etiketter eller kategorier som tilldelats korpusen.
För att extrahera och förstå mönster från dokumenten följer LSA till sin natur vissa antaganden:
1) Betydelsen av meningar eller dokument är en summa av betydelsen av alla ord som förekommer i dem. Totalt sett är betydelsen av ett visst ord ett genomsnitt av alla dokument som det förekommer i.
2) LSA utgår från att de semantiska associationerna mellan ord inte finns uttryckligen utan endast latent i det stora urvalet av språk.
Matematiska perspektiv
Latent semantisk analys (LSA) består av vissa matematiska operationer för att få en inblick i ett dokument. Denna algoritm utgör grunden för Topic Modeling. Kärnidén är att ta en matris av det vi har – dokument och termer – och dekomponera den till en separat dokument-ämnesmatris och en ämnes-term-matris.
Det första steget är att generera vår dokument-term-matris med hjälp av Tf-IDF Vectorizer. Den kan också konstrueras med hjälp av en Bag-of-Words-modell, men resultaten är sparsamma och ger ingen betydelse för saken.
Givet m dokument och n-ord i vårt vokabulär kan vi konstruera en
m × n-matris A där varje rad representerar ett dokument och varje kolumn representerar ett ord.
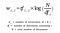
Intuitivt har en term en stor vikt när den förekommer ofta i dokumentet men sällan i korpusen.
Vi bildar en matris för dokumenttermer, A, med hjälp av denna omvandlingsmetod (tf-IDF) för att vektorisera vår korpus. ( På ett sätt som vår fortsatta modell kan bearbeta eller utvärdera eftersom vi ännu inte arbetar med strängar!).
Men det finns en subtil nackdel, vi kan inte dra några slutsatser genom att observera A, eftersom det är en brusig och gles matris. ( Ibland för stor för att ens beräkna för vidare processer).
Då Topic Modeling till sin natur är en oövervakad algoritm, måste vi specificera de latenta ämnena i förväg. Det är analogt med K-Means Clustering så att vi specificerar antalet kluster i förväg.
I det här fallet utför vi en Low-Rank Approximation med hjälp av en teknik för dimensionalitetsreducering med hjälp av en Truncated Singular Value Decomposition (SVD).
Singular value decomposition är en teknik inom linjär algebra som faktoriserar en matris M till produkten av 3 separata matriser: M=U*S*V, där S är en diagonalmatris med M:s singulära värden.
Truncated SVD reducerar dimensionaliteten genom att endast välja de t största singulära värdena och endast behålla de första t kolumnerna i U och V. I det här fallet är t en hyperparameter som vi kan välja och justera för att återspegla antalet ämnen som vi vill hitta.
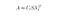
Notera: Truncated SVD gör dimensionalitetsminskningen och inte SVD!

Med dessa dokumentvektorer och termvektorer kan vi nu enkelt tillämpa mått som cosinuslikhet för att utvärdera:
- likheten mellan olika dokument
- likheten mellan olika ord
- likheten mellan termer (eller ”förfrågningar”) och dokument (vilket blir användbart vid informationssökning, när vi vill hämta de avsnitt som är mest relevanta för vår sökfråga).
Slutanmärkningar
Denna algoritm används främst i olika NLP-baserade uppgifter och ligger till grund för mer robusta metoder som Probabilistisk LSA och Latent Dirichlet Allocation (LDA).
Kushal Vala, Junior Data Scientist at Datametica Solutions Pvt Ltd