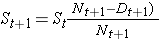Vi är ofta intresserade av att bedöma om det finns skillnader i överlevnad (eller kumulativ förekomst av händelser) mellan olika grupper av deltagare. I en klinisk prövning med ett överlevnadsutfall kan vi till exempel vara intresserade av att jämföra överlevnaden mellan deltagare som får ett nytt läkemedel jämfört med placebo (eller standardbehandling). I en observationsstudie kan vi vara intresserade av att jämföra överlevnad mellan män och kvinnor, eller mellan deltagare med och utan en viss riskfaktor (t.ex. högt blodtryck eller diabetes). Det finns flera tester för att jämföra överlevnad mellan oberoende grupper.
Log Rank Test
Log Rank Testet är ett populärt test för att testa nollhypotesen att det inte finns någon skillnad i överlevnad mellan två eller flera oberoende grupper. Testet jämför hela överlevnadsupplevelsen mellan grupperna och kan ses som ett test av om överlevnadskurvorna är identiska (överlappande) eller inte. Överlevnadskurvorna uppskattas för varje grupp, betraktad separat, med hjälp av Kaplan-Meier-metoden och jämförs statistiskt med hjälp av logrank-testet. Det är viktigt att notera att det finns flera varianter av statistiken för logrank-testet som genomförs av olika statistiska datapaket (t.ex. SAS, R 4,6). Vi presenterar här en version som är nära kopplad till chi-square-teststatistiken och jämför det observerade med det förväntade antalet händelser vid varje tidpunkt under uppföljningsperioden.
Exempel:
En liten klinisk prövning genomförs för att jämföra två kombinationsbehandlingar hos patienter med avancerad magsäckscancer. Tjugo deltagare med magsäckscancer i stadium IV som samtycker till att delta i studien tilldelas slumpmässigt kemoterapi före operation eller kemoterapi efter operation. Det primära utfallet är dödsfall och deltagarna följs upp till 48 månader (4 år) efter inskrivning i studien. Erfarenheterna av deltagarna i varje del av studien visas nedan.
|
Kemoterapi före operation |
|
Kemoterapi efter operation |
||
|---|---|---|---|---|
|
Månad. Död |
Månad för sista kontakt |
|
Månad för död |
Månad för sista kontakt |
|
8 |
8 |
|
33 |
48 |
|
12 |
32 |
|
28 |
48 |
|
26 |
20 |
|
41 |
25 |
|
14 |
40 |
|
|
37 |
|
21 |
|
|
|
48 |
|
27 |
|
|
|
25 |
|
|
|
|
|
43 |
Sex deltagare i gruppen kemoterapi före kirurgi dör under uppföljningen.Uppföljning jämfört med tre deltagare i gruppen med kemoterapi efter operation. Övriga deltagare i varje grupp följs i olika antal månader, vissa till studiens slut vid 48 månader (i gruppen med kemoterapi efter kirurgi). Med hjälp av de förfaranden som beskrivs ovan konstruerar vi först livstabeller för varje behandlingsgrupp med hjälp av Kaplan-Meier-metoden.
Livstabell för gruppen som får kemoterapi före operation
|
Tid, Månader |
Antal i riskzonen Nt |
Antal dödsfall Dt |
Antal censurerade Ct |
Sannolikhet för överlevnad
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
8 |
10 |
1 |
1 |
0.900 |
|
12 |
8 |
1 |
|
0.788 |
|
14 |
7 |
1 |
|
0.675 |
|
20 |
6 |
|
1 |
0.675 |
|
21 |
5 |
1 |
|
0.540 |
|
26 |
4 |
1 |
|
0.405 |
|
27 |
3 |
1 |
|
0.270 |
|
32 |
2 |
|
1 |
0.270 |
|
40 |
1 |
|
1 |
0.270 |
Livstabell för gruppen som får kemoterapi efter kirurgi
|
Tid, Månader |
Antal i riskzonen Nt |
Antal dödsfall Dt |
Antal censurerade Ct |
Sannolikhet för överlevnad
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
25 |
10 |
|
2 |
1.000 |
|
28 |
8 |
1 |
|
0.875 |
|
33 |
7 |
1 |
|
0.750 |
|
37 |
6 |
|
1 |
0.750 |
|
41 |
5 |
1 |
|
0.600 |
|
43 |
4 |
|
1 |
0.600 |
|
48 |
3 |
|
3 |
0.600 |
De två överlevnadskurvorna visas nedan.
Överlevnad i varje behandlingsgrupp
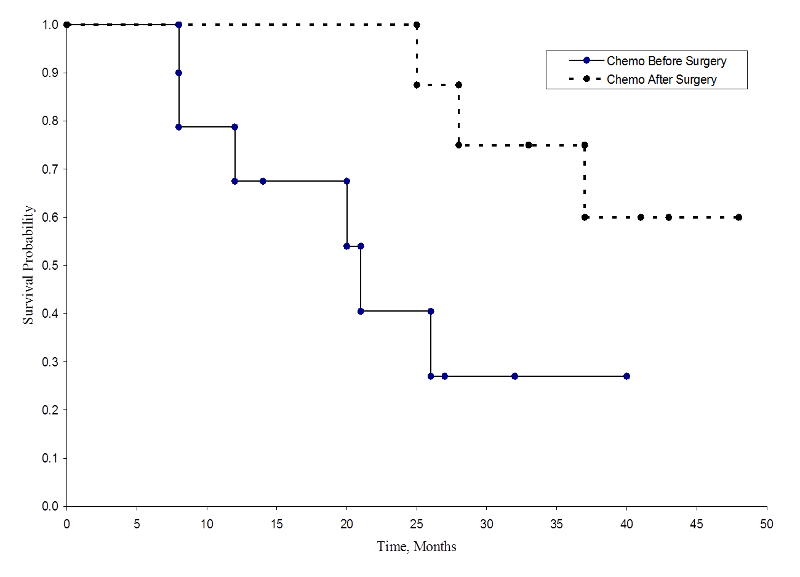
Överlevnadssannolikheterna för gruppen med kemoterapi efter operation är högre än överlevnadssannolikheterna för gruppen med kemoterapi före operation, vilket tyder på en överlevnadsfördel. Dessa överlevnadskurvor är dock uppskattade från små urval. För att jämföra överlevnaden mellan grupperna kan vi använda logrank-testet. Nollhypotesen är att det inte finns någon skillnad i överlevnad mellan de två grupperna eller att det inte finns någon skillnad mellan populationerna i sannolikheten att dö vid någon tidpunkt. Logrank-testet är ett icke-parametriskt test och gör inga antaganden om överlevnadsfördelningarna. I huvudsak jämför logrank-testet det observerade antalet händelser i varje grupp med vad som skulle förväntas om nollhypotesen var sann (dvs, om överlevnadskurvorna var identiska).
H0: De två överlevnadskurvorna är identiska (eller S1t = S2t) kontra H1: De två överlevnadskurvorna är inte identiska (eller S1t ≠ S2t, vid vilken tidpunkt som helst t) (α = 0,05).
Log rank-statistiken är ungefärligt fördelad som en chi-square teststatistik. Det finns flera former av teststatistiken, och de varierar när det gäller hur de beräknas. Vi använder följande:
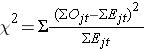
där ΣOjt representerar summan av det observerade antalet händelser i den j:e gruppen över tiden (t.ex. j=1,2) och ΣEjt representerar summan av det förväntade antalet händelser i den j:e gruppen över tiden.
Summorna av det observerade och det förväntade antalet händelser beräknas för varje tidpunkt för händelsen och summeras för varje jämförelsegrupp. Logrank-statistiken har frihetsgrader som är lika med k-1, där k representerar antalet jämförelsegrupper. I detta exempel är k=2 så teststatistiken har 1 frihetsgrad.
För att beräkna teststatistiken behöver vi det observerade och förväntade antalet händelser vid varje händelsetid. Det observerade antalet händelser kommer från urvalet och det förväntade antalet händelser beräknas genom att anta att nollhypotesen är sann (dvs. att överlevnadskurvorna är identiska).
För att generera det förväntade antalet händelser organiserar vi data i en livstabell med rader som representerar varje händelsetidpunkt, oberoende av i vilken grupp händelsen inträffade. Vi håller också reda på grupptilldelningen. Vi uppskattar sedan andelen händelser som inträffar vid varje tidpunkt (Ot/Nt) med hjälp av data från båda grupperna tillsammans under antagandet att det inte finns någon skillnad i överlevnad (dvs. att nollhypotesen är sann). Vi multiplicerar dessa skattningar med antalet deltagare i riskzonen vid den tidpunkten i var och en av jämförelsegrupperna (N1t och N2t för grupp 1 respektive 2).
Specifikt beräknar vi för varje händelsetidpunkt t antalet deltagare i riskzonen i varje grupp, Njt (t.ex. där j anger gruppen, j=1, 2) och antalet händelser (dödsfall), Ojt ,i varje grupp. Tabellen nedan innehåller den information som behövs för att genomföra logrank-testet för att jämföra överlevnadskurvorna ovan. Grupp 1 representerar gruppen med kemoterapi före operation och grupp 2 representerar gruppen med kemoterapi efter operation.
Data för Log Rank Test för att jämföra överlevnadskurvor
|
Tid, Månader |
Antal i riskgrupp 1
N1t |
Antal i riskgrupp 2
N2t |
Antal händelser (dödsfall) i grupp 1
O1t |
Antal Antal händelser (dödsfall) i grupp 2
O2t |
|---|---|---|---|---|
|
8 |
10 |
10 |
1 |
0 |
|
12 |
8 |
10 |
1 |
0 |
|
14 |
7 |
10 |
1 |
0 |
|
21 |
5 |
10 |
1 |
0 |
|
26 |
4 |
8 |
1 |
0 |
|
27 |
3 |
8 |
1 |
0 |
|
28 |
2 |
8 |
0 |
1 |
|
33 |
1 |
7 |
0 |
1 |
|
41 |
0 |
5 |
0 |
1 |
Därefter summerar vi antalet i riskzonen, Nt = N1t+N2t, vid varje händelsetidpunkt och antalet observerade händelser (dödsfall), Ot = O1t+O2t, vid varje händelsetidpunkt. Vi beräknar sedan det förväntade antalet händelser i varje grupp. Det förväntade antalet händelser beräknas för varje händelsetidpunkt enligt följande:
E1t = N1t*(Ot/Nt) för grupp 1 och E2t = N2t*(Ot/Nt) för grupp 2. Beräkningarna visas i tabellen nedan.
Förväntat antal händelser i varje grupp
|
Tid, Månader |
Antal i riskgrupp 1 N1t |
Antal i riskgrupp 2 N2t |
Totalt antal i riskgrupp Nt |
Antal händelser i grupp 1 O1t |
Antal händelser i grupp 2 O2t |
Total antal händelser Ot |
Förväntat antal händelser i Grupp 1 E1t = N1t*(Ot/Nt) |
Förväntat antal händelser i Grupp 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
Därefter summerar vi det observerade antalet händelser i varje grupp (∑O1t och ΣO2t) och det förväntade antalet händelser i varje grupp (ΣE1t och ΣE2t) över tiden. Dessa visas i den nedersta raden i nästa tabell nedan.
Total observerat och förväntat antal observerade i varje grupp
|
Tid, Månader |
Antal i riskgrupp 1 N1t |
Antal i riskgrupp 2 N2t |
Totalt antal i riskgrupp Nt |
Antal händelser i grupp 1 O1t |
Antal händelser i grupp 2 O2t |
Totalt antal händelser Ot |
Förväntat antal händelser i Grupp 1 E1t = N1t*(Ot/Nt) |
Förväntat antal händelser i Grupp 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
6 |
3 |
|
2.620 |
6.380 |
Vi kan nu beräkna teststatistiken:
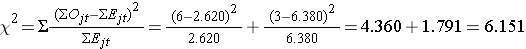
Teststatistiken är ungefärligt fördelad som chi-två med 1 frihetsgrad. Det kritiska värdet för testet kan således hittas i tabellen Critical Values of the Χ2 Distribution.
För detta test är beslutsregeln att förkasta H0 om Χ2 > 3,84. Vi observerar Χ2 = 6,151, vilket överstiger det kritiska värdet 3,84. Därför förkastar vi H0. Vi har signifikanta bevis, α=0,05, som visar att de två överlevnadskurvorna är olika.
Exempel:
En forskare vill utvärdera effekten av en kort intervention för att förebygga alkoholkonsumtion under graviditeten. Gravida kvinnor med en historia av hög alkoholkonsumtion rekryteras till studien och randomiseras till att få antingen den korta interventionen med fokus på avhållsamhet från alkohol eller vanlig prenatal vård. Det intressanta utfallet är återfall i drickande. Kvinnor rekryteras till studien vid cirka 18 veckors graviditet och följs under hela graviditeten fram till förlossningen (cirka 39 veckors graviditet). Uppgifterna visas nedan och anger om kvinnorna återfaller i drickande och i så fall tidpunkten för deras första drickande, mätt i antal veckor från randomiseringen. För kvinnor som inte återfaller i drickande registrerar vi antalet veckor från randomiseringen som de är alkoholfria.
|
Standardiserad förlossningsvård |
|
Kort intervention |
|||
|---|---|---|---|---|---|
|
Rebell |
Inget återfall |
|
Rebell |
Inget återfall |
Inget återfall |
|
19 |
20 |
|
16 |
21 |
|
|
6 |
19 |
|
21 |
15 |
|
|
5 |
17 |
|
7 |
18 |
|
|
4 |
14 |
|
|
18 |
|
|
|
|
|
|
5 |
|
Frågan som är av intresse är om det finns en skillnad i tid till återfall mellan kvinnor som tilldelats standardförlossningsvård jämfört med kvinnor som tilldelats den korta interventionen.
- Steg 1.
Sätt upp hypoteser och bestäm signifikansnivån.
H0: Den återfallsfria tiden är identisk mellan grupperna jämfört med
H1: Den återfallsfria tiden är inte identisk mellan grupperna (α=0,05)
- Steg 2.
Välj lämplig teststatistik.
Teststatistiken för logrank-testet är
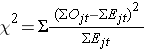
- Steg 3.
Sätt upp beslutsregeln.
Teststatistiken följer en chi-två-fördelning och därför hittar vi det kritiska värdet i tabellen över kritiska värden för Χ2-fördelningen) för df=k-1=2-1=1 och α=0,05. Det kritiska värdet är 3,84 och beslutsregeln är att förkasta H0 om Χ2 > 3,84.
- Steg 4.
Beräkna teststatistiken.
För att beräkna teststatistiken organiserar vi data enligt händelsetidpunkter (återfall) och bestämmer antalet kvinnor i riskzonen i varje behandlingsgrupp och antalet som återfaller vid varje observerad återfallstidpunkt. I följande tabell representerar grupp 1 kvinnor som får vanlig förlossningsvård och grupp 2 kvinnor som får den korta interventionen.
|
Tid, Veckor |
Antal i riskzonen – Grupp 1 N1t |
Antal i riskzonen – Grupp 2 N2t |
Antal återfall – Grupp 1 O1t |
Antal återfall – Grupp 1 O1t |
Antal återfall – Grupp 1 Grupp 2 O2t |
|---|---|---|---|---|---|
|
4 |
8 |
8 |
8 |
1 |
0 |
|
5 |
7 |
8 |
1 |
0 |
|
|
6 |
6 |
7 |
1 |
0 |
|
|
7 |
5 |
7 |
0 |
1 |
|
|
16 |
4 |
5 |
0 |
1 |
|
|
19 |
3 |
2 |
1 |
0 |
|
|
21 |
0 |
2 |
0 |
1 |
Vi summerar sedan antalet risktagare, 
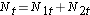, vid varje händelsetillfälle, antalet observerade händelser (återfall), 
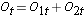, vid varje händelsetillfälle och bestämmer det förväntade antalet återfall i varje grupp vid varje händelsetillfälle med hjälp av 
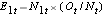och 
.
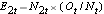Vi summerar sedan det observerade antalet händelser i varje grupp (ΣO1t och ΣO2t) och det förväntade antalet händelser i varje grupp (ΣE1t och ΣE2t) över tiden. Beräkningarna för uppgifterna i detta exempel visas nedan.
| Time, Veckor |
Antal i riskgrupp 1 N1t |
Antal i riskgrupp 2 N2t |
Total antal i riskgrupp Nt |
Antal återfall Grupp 1 O1t |
Antal återfall Grupp 2 O2t |
Totalt antal återfall Ot |
Förväntat antal återfall i grupp 1
|
Förväntat antal återfall i grupp 2
|
|---|---|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
16 |
1 |
0 |
1 |
0.500 |
0.500 |
|
5 |
7 |
8 |
15 |
1 |
0 |
1 |
0.467 |
0.533 |
|
6 |
6 |
7 |
13 |
1 |
0 |
1 |
0.462 |
0.538 |
|
7 |
5 |
7 |
12 |
0 |
1 |
1 |
0.417 |
0.583 |
|
16 |
4 |
5 |
9 |
0 |
1 |
1 |
0.444 |
0.556 |
|
19 |
3 |
2 |
5 |
1 |
0 |
1 |
0.600 |
0.400 |
|
21 |
0 |
2 |
2 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
|
|
|
4 |
3 |
|
2.890 |
4.110 |
Vi beräknar nu teststatistiken:
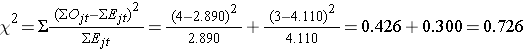
- Steg 5.
Slutsats. Förkasta inte H0 eftersom 0,726 < 3,84. Vi har inget statistiskt signifikant bevis vid α=0,05 för att visa att tiden till återfall skiljer sig mellan grupperna.
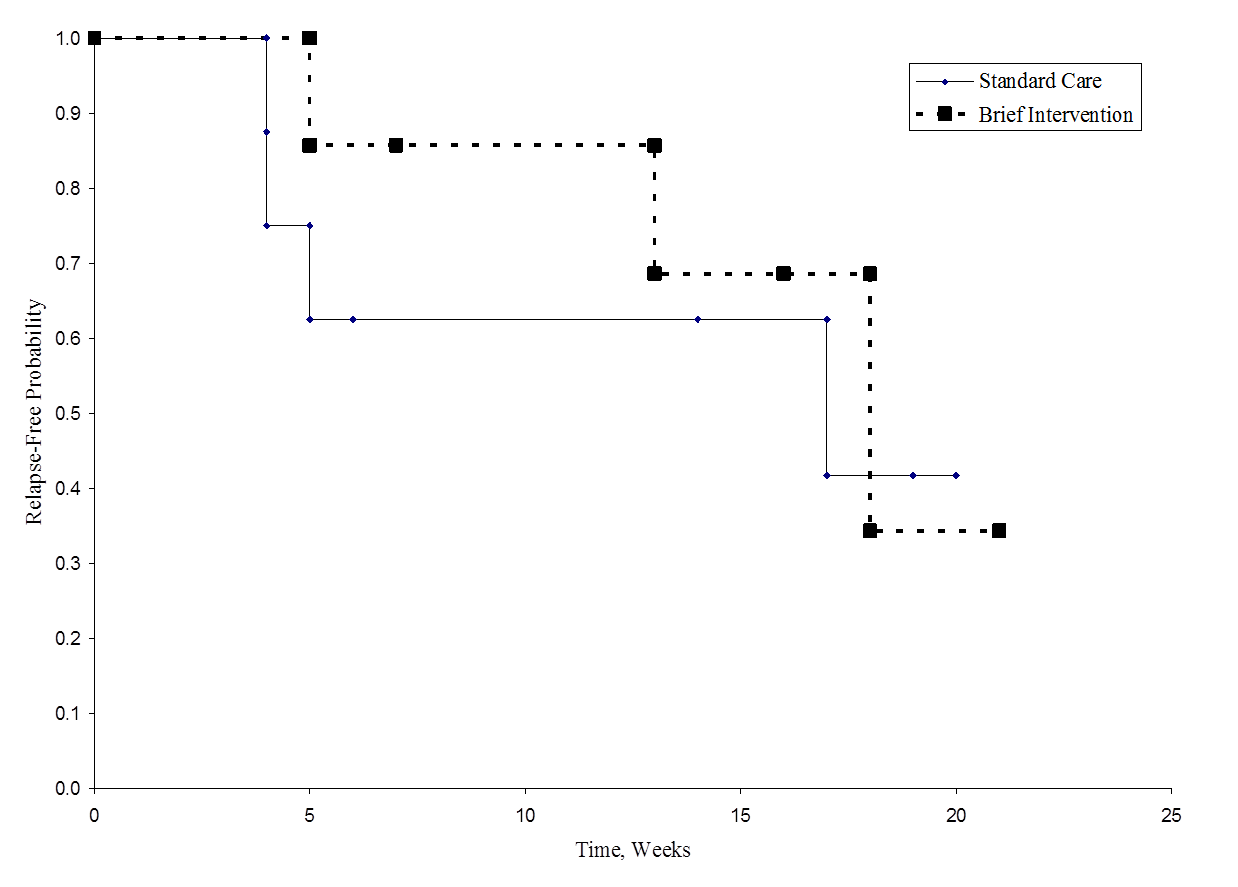
Figuren nedan visar överlevnaden (återfallsfri tid) i varje grupp. Lägg märke till att överlevnadskurvorna inte visar någon större åtskillnad, vilket överensstämmer med de icke-signifikanta resultaten i hypotesprövningen.
Relapse-Free Time in Each Group
Som nämnts finns det flera olika varianter av log rank-statistiken. Vissa statistiska beräkningspaket använder följande teststatistik för logrank-testet för att jämföra två oberoende grupper:
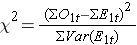
där ΣO1t är summan av det observerade antalet händelser i grupp 1, och ΣE1t är summan av det förväntade antalet händelser i grupp 1 taget över alla händelsetider. Nämnaren är summan av varianserna för det förväntade antalet händelser vid varje händelsetidpunkt, som beräknas på följande sätt:
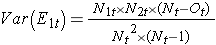
Det finns andra versioner av logrankstatistiken samt andra tester för att jämföra överlevnadsfunktioner mellan oberoende grupper.7-9 Ett populärt test är till exempel det modifierade Wilcoxon-testet som är känsligt för större skillnader i risker tidigare jämfört med senare i uppföljningen.10
Tillbaka till början | föregående sida | nästa sida