
Och även om, som nämns i avsnittet Signalflödesanalys, någon form av signalflödesanalys är det mest allmänna sättet att behandla den negativa återkopplingsförstärkaren, är representation som två två tvåportar det tillvägagångssätt som oftast presenteras i läroböcker och som presenteras här. Den bibehåller en kretsuppdelning av förstärkaren i två block, men tillåter att blocken är bilaterala. Vissa nackdelar med denna metod beskrivs i slutet.
Elektroniska förstärkare använder ström eller spänning som ingång och utgång, så fyra typer av förstärkare är möjliga (någon av två möjliga ingångar med någon av två möjliga utgångar). Se klassificering av förstärkare. Målet för återkopplingsförstärkaren kan vara vilken som helst av de fyra typerna av förstärkare och är inte nödvändigtvis av samma typ som den öppna förstärkaren, som i sin tur kan vara vilken som helst av dessa typer. Så till exempel kan en op-förstärkare (spänningsförstärkare) arrangeras så att den i stället blir en strömförstärkare.
Negativa återkopplingsförstärkare av vilken typ som helst kan genomföras med hjälp av kombinationer av nätverk med två portar. Det finns fyra typer av tvåportsnätverk, och den typ av förstärkare som önskas dikterar valet av tvåportar och valet av en av de fyra olika anslutningstopologier som visas i diagrammet. Dessa anslutningar kallas vanligen för serie- eller shuntförbindelser (parallella). I diagrammet visar den vänstra kolumnen shuntingångar och den högra kolumnen serieingångar. Den övre raden visar serieutgångar; den nedre raden visar shuntutgångar. De olika kombinationerna av anslutningar och två portar anges i tabellen nedan.
| Typ av återkopplingsförstärkare | Inputsanslutning | Outputsanslutning | Ideal återkoppling | Två-portåterkoppling |
|---|---|---|---|---|
| Styrka | Shunt | Serie | ||
| Transkonduktans | Serie | Serie | VCCS | z-parameter |
| Serie | Shunt | h-parameter |
Till exempel, För en strömåterkopplingsförstärkare samplas strömmen från utgången för återkoppling och kombineras med strömmen vid ingången. Därför utförs återkopplingen idealt sett med hjälp av en (utgående) strömstyrd strömkälla (CCCS), och dess ofullkomliga förverkligande med hjälp av ett nätverk med två portar måste också innehålla en CCCS, det vill säga det lämpliga valet för återkopplingsnätverket är en g-parameter med två portar. Här presenteras den tvåportsmetod som används i de flesta läroböcker, med hjälp av den krets som behandlas i artikeln om asymptotisk förstärkningsmodell.

Figur 3 visar en förstärkare med två transistorer och med ett återkopplingsmotstånd Rf. Syftet är att analysera denna krets för att hitta tre saker: förstärkningen, utgångsimpedansen när man tittar in i förstärkaren från belastningen och ingångsimpedansen när man tittar in i förstärkaren från källan.
- Ersättande av återkopplingsnätverket med en tvåportRedigera
- Krets med små signalerRedigera
- Laddad open-loop-förstärkningRedigera
- Förstärkning med återkopplingRedigera
- Ingångs- och utgångsresistanserRedigera
- Bakgrund till bestämmandet av motstånd Redigera
- Tillämpning på exempelförstärkarenRedigera
- Lastspänning och lastströmRedigera
- Är huvudförstärkarblocket ett tvåportsblock?Edit
Ersättande av återkopplingsnätverket med en tvåportRedigera
Det första steget är att ersätta återkopplingsnätverket med en tvåport. Vilka komponenter ingår i tvåporten?
På ingångssidan av tvåporten har vi Rf. Om spänningen på höger sida av Rf ändras, ändras strömmen i Rf som subtraheras från den ström som går in i basen på ingångstransistorn. Det vill säga, ingångssidan av tvåporten är en beroende strömkälla som styrs av spänningen vid toppen av motstånd R2.
Man skulle kunna säga att förstärkarens andra steg bara är en spänningsföljare, som överför spänningen vid kollektorn på ingångstransistorn till toppen av R2. Det vill säga, den övervakade utsignalen är egentligen spänningen vid kollektorn på ingångstransistorn. Det synsättet är legitimt, men då blir spänningsföljarsteget en del av återkopplingsnätverket. Det gör analysen av återkoppling mer komplicerad.
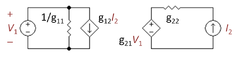
En alternativ synpunkt är att spänningen vid toppen av R2 ställs in av emitterströmmen i utgångstransistorn. Det synsättet leder till ett helt passivt återkopplingsnätverk som består av R2 och Rf. Den variabel som styr återkopplingen är emitterströmmen, så återkopplingen är en strömstyrd strömkälla (CCCS). Vi söker igenom de fyra tillgängliga tvåportsnätverken och finner att det enda med en CCCS är g-parameterns tvåportsnätverk, som visas i figur 4. Nästa uppgift är att välja g-parametrarna så att tvåporten i figur 4 är elektriskt likvärdig med L-sektionen som består av R2 och Rf. Detta val är ett algebraiskt förfarande som görs enklast genom att titta på två enskilda fall: fallet med V1 = 0, vilket gör VCVS på höger sida av tvåporten till en kortslutning, och fallet med I2 = 0, vilket gör CCCS på vänster sida till en öppen krets. Algebran i dessa två fall är enkel, mycket enklare än att lösa för alla variabler på en gång. Valet av g-parametrar som gör att tvåporten och L-sektionen beter sig på samma sätt visas i tabellen nedan.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{\mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 + R f {\displaystyle -{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 R 2 + R f {\displaystyle {\frac {R_{2}}{R_{2}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
 |
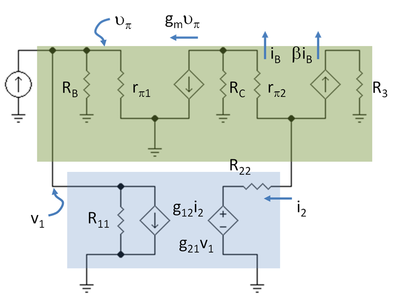
Krets med små signalerRedigera
Nästa steg är att rita ett schema med små signaler för förstärkaren med tvåporten på plats med hjälp av hybrid-pi-modellen för transistorerna. Figur 5 visar schemat med notation R3 = RC2 // RL och R11 = 1 / g11, R22 = g22.
Laddad open-loop-förstärkningRedigera
Figur 3 anger utgångsnoden, men inte valet av utgångsvariabel. Ett användbart val är förstärkarens kortslutningsströmsutgång (vilket leder till kortslutningsströmsförstärkningen). Eftersom denna variabel helt enkelt leder till något av de andra valen (t.ex. belastningsspänning eller belastningsström), hittas kortslutningsströmsförstärkningen nedan.
Först hittas den belastade open-loop-förstärkningen. Återkopplingen stängs av genom att ställa in g12 = g21 = 0. Tanken är att hitta hur mycket förstärkarförstärkningen ändras på grund av motstånden i återkopplingsnätverket av sig själva, med återkopplingen avstängd. Denna beräkning är ganska enkel eftersom R11, RB och rπ1 alla är parallella och v1 = vπ. Låt R1 = R11 // RB // rπ1. Dessutom ska i2 = -(β+1) iB. Resultatet för strömförstärkningen AOL med öppen loop är:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\displaystyle A_{\mathrm {OL} }={\frac {\beta i_{\mathrm {B}} }}}{i_{\mathrm {S}}} }}}=g_{m}R_{\mathrm {C} }\left({\frac {\beta }{\beta +1}}\right)\left({\frac {R_{1}}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C} }}{\beta +1}}}}\right)\ .}

Förstärkning med återkopplingRedigera
I det klassiska tillvägagångssättet för återkoppling försummas den återkoppling som representeras av VCVS (dvs. g21 v1). Det gör att kretsen i figur 5 liknar blockdiagrammet i figur 1, och förstärkningen med återkoppling är då:
A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{{\mathrm {FB}} }={\frac {A_{\mathrm {OL} }}{1+{\frac {R_{2}}}{R_{2}+R_{\mathrm {f} }}}A_{{\mathrm {OL}} }}}}\\ ,}

där återkopplingsfaktorn βFB = -g12. Notation βFB införs för återkopplingsfaktorn för att skilja den från transistorn β.
Ingångs- och utgångsresistanserRedigera

Råterkoppling används för att bättre matcha signalkällorna till deras belastningar. Till exempel kan en direkt anslutning av en spänningskälla till en resistiv belastning resultera i signalförlust på grund av spänningsdelning, men genom att lägga in en negativ återkopplingsförstärkare kan man öka den skenbara belastning som ses av källan och minska den skenbara drivningsimpedansen som ses av belastningen, vilket gör att man undviker signaldämpningen på grund av spänningsdelning. Denna fördel är inte begränsad till spänningsförstärkare, utan analoga förbättringar av matchningen kan ordnas för strömförstärkare, transkonduktansförstärkare och transresistansförstärkare.
För att förklara dessa återkopplingseffekter på impedanserna krävs först en utvikning om hur tvåportsteorin närmar sig bestämmandet av motståndet, och sedan dess tillämpning på den aktuella förstärkaren.
Bakgrund till bestämmandet av motstånd Redigera
Figur 6 visar en ekvivalentkrets för att hitta ingångsresistansen för en återkopplad spänningsförstärkare (till vänster) och för en återkopplad strömförstärkare (till höger). Dessa arrangemang är typiska tillämpningar av Miller-satsen.
I fallet med spänningsförstärkaren läggs återkopplingsnätverkets utgångsspänning βVout i serie och med motsatt polaritet till ingångsspänningen Vx som färdas över slingan (men i förhållande till jord är polariteterna desamma). Som ett resultat av detta minskar den effektiva spänningen över och strömmen genom förstärkarens ingångsresistans Rin så att kretsens ingångsresistans ökar (man skulle kunna säga att Rin uppenbarligen ökar). Dess nya värde kan beräknas genom att tillämpa Miller-satsen (för spänningar) eller de grundläggande kretslagarna. Kirchhoffs spänningslag ger således:
V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} }+\beta v_{\mathrm {out} }\ ,}

varvid vout = Av vin = Av Ix Rin. Genom att sätta in detta resultat i ovanstående ekvation och lösa för återkopplingsförstärkarens ingångsresistans blir resultatet:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}}=\left(1+\beta A_{v}\right)R_{\mathrm {in} }\ .}

Den allmänna slutsatsen från detta exempel och ett liknande exempel för fallet med utgångsresistans är: En serieåterkopplingsförbindelse vid ingången (utgången) ökar ingångsresistansen (utgångsresistansen) med en faktor ( 1 + β AOL ), där AOL = förstärkning av den öppna slingan.
För strömförstärkaren å andra sidan, för återkopplingsnätverkets utgångsström βIout, appliceras parallellt och med motsatt riktning till ingångsströmmen Ix. Som ett resultat av detta ökar den totala strömmen som flyter genom kretsens ingång (inte bara genom ingångsmotståndet Rin) och spänningen över den minskar så att kretsens ingångsmotstånd minskar (Rin minskar tydligen). Dess nya värde kan beräknas genom att tillämpa den dubbla Miller-satsen (för strömmar) eller Kirchhoffs grundläggande lagar:
I x = V i n R i n + β i o u t . {\displaystyle I_{x}={\frac {V_{\mathrm {in} }}{R_{{\mathrm {in} }}}+\beta i_{{\mathrm {out}} }\ .}

varvid iout = Ai iin = Ai Vx / Rin. Genom att ersätta detta resultat med ovanstående ekvation och lösa för återkopplingsförstärkarens ingångsmotstånd blir resultatet:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}}{I_{x}}}={\frac {R_{\mathrm {in}}} }}}{\left(1+\beta A_{i}\right)}}\ .}

Den allmänna slutsatsen från detta exempel och ett liknande exempel för fallet med utgångsresistans är:En parallell återkopplingsförbindelse vid ingången (utgången) minskar ingångsresistansen (utgångsresistansen) med en faktor ( 1 + β AOL ), där AOL = förstärkning av öppen slinga.
Dessa slutsatser kan generaliseras för att behandla fall med godtyckliga Norton- eller Thévenin-drifter, godtyckliga belastningar och allmänna återkopplingsnätverk med två portar. Resultaten är dock beroende av att huvudförstärkaren representeras som ett tvåportssystem – det vill säga resultaten är beroende av att samma ström går in i och ut ur ingångsterminalerna, och på samma sätt måste samma ström som lämnar en utgångsterminal gå in i den andra utgångsterminalen.
En bredare slutsats, oberoende av de kvantitativa detaljerna, är att återkoppling kan användas för att öka eller minska ingångs- och utgångsimpedansen.
Tillämpning på exempelförstärkarenRedigera
Dessa motståndsresultat tillämpas nu på förstärkaren i figur 3 och figur 5. Förbättringsfaktorn som minskar förstärkningen, nämligen ( 1 + βFB AOL), avgör direkt effekten av återkoppling på förstärkarens ingångs- och utgångsresistanser. Vid shuntkoppling minskas ingångsimpedansen med denna faktor, och vid seriekoppling multipliceras impedansen med denna faktor. Den impedans som ändras av återkopplingen är dock impedansen hos förstärkaren i figur 5 med återkopplingen avstängd, och inkluderar de ändringar av impedansen som orsakas av motstånden i återkopplingsnätverket.
Därmed är ingångsimpedansen som ses av källan när återkopplingen är avstängd Rin = R1 = R11 // RB // rπ1, och när återkopplingen är påslagen (men ingen feedforward)
R i n = R 1 1 1 + β F B A O L , {\displaystyle R_{\mathrm {in} }={\frac {R_{1}}}{1+{\beta }_{\mathrm {FB} }A_{{\mathrm {OL} }}}}\ ,}

där division används eftersom ingångsanslutningen är shunt: den återkopplade tvåporten är parallell med signalkällan på förstärkarens ingångssida. En påminnelse: AOL är den belastade open loop-förstärkningen som hittats ovan, modifierad av motstånden i återkopplingsnätverket.
Den impedans som ses av belastningen behöver diskuteras ytterligare. Lasten i figur 5 är ansluten till utgångstransistorens kollektor och är därför separerad från förstärkarens kropp genom utgångsströmkällans oändliga impedans. Därför har återkoppling ingen effekt på utgångsimpedansen, som förblir helt enkelt RC2 som ses av belastningsmotståndet RL i figur 3.
Om vi i stället ville hitta impedansen som presenteras vid emittern av utgångstransistorn (i stället för dess kollektor), som är seriekopplad till återkopplingsnätverket, skulle återkoppling öka detta motstånd med förbättringsfaktorn ( 1 + βFB AOL).
Lastspänning och lastströmRedigera
Den förstärkning som härletts ovan är strömförstärkningen vid utgångstransistorens kollektor. För att relatera denna förstärkning till förstärkningen när spänning är förstärkarens utgång, observera att utgångsspänningen vid belastningen RL är relaterad till kollektorströmmen enligt Ohms lag som vL = iC (RC2 || RL). Följaktligen fås transresistansförstärkningen vL / iS genom att multiplicera strömförstärkningen med RC2 || RL:
v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{\mathrm {L} }}}{i_{\mathrm {S}}{i_{\mathrm {S}}}{i_{\mathrm {S}} }}}=A_{{\mathrm {FB}} }(R_{\mathrm {C2} }\parallel R_{\mathrm {L} })\ .}

Samma gäller om förstärkarens utgång antas vara strömmen i belastningsmotståndet RL, så bestämmer strömdivisionen belastningsströmmen och förstärkningen blir då:
i L i S = A F B R C 2 R C 2 R C 2 + R L . {\displaystyle {\frac {i_{\mathrm {L} }}{i_{\mathrm {S} }}}=A_{{\mathrm {FB}}=A_{\mathrm {FB}} }{\frac {R_{{\mathrm {C2}} }}{R_{\mathrm {C2} }+R_{\\mathrm {L}} }}}\ .}

Är huvudförstärkarblocket ett tvåportsblock?Edit

Några nackdelar med metoden med två två portar följer, avsedda för den uppmärksamme läsaren.
Figur 7 visar småsignalschemat med huvudförstärkaren och den återkopplade tvåporten i skuggade rutor. Den återkopplade tvåporten uppfyller portvillkoren: vid ingångsporten går Iin in och ut ur porten, och likaså vid utgången går Iout in och ut.
Är huvudförstärkarblocket också en tvåport? Huvudförstärkaren visas i den övre skuggade rutan. Jordanslutningarna är märkta. Figur 7 visar det intressanta faktum att huvudförstärkaren inte uppfyller portvillkoren vid sin ingång och utgång om inte jordförbindelserna väljs så att detta sker. På ingångssidan är t.ex. strömmen som går in i huvudförstärkaren IS. Denna ström delas upp på tre sätt: till återkopplingsnätverket, till förspänningsmotståndet RB och till ingångstransistorens basmotstånd rπ. För att uppfylla portvillkoret för huvudförstärkaren måste alla tre komponenterna återföras till huvudförstärkarens ingångssida, vilket innebär att alla jordledningar märkta G1 måste anslutas, liksom emitterledningen GE1. På samma sätt måste på utgångssidan alla jordanslutningar G2 anslutas och även jordanslutning GE2. Sedan, längst ner i schemat, under återkopplingstvåporten och utanför förstärkarblocken, är G1 ansluten till G2. Detta tvingar jordströmmarna att fördela sig mellan ingångs- och utgångssidan som planerat. Lägg märke till att detta anslutningsarrangemang delar upp emittern på ingångstransistorn i en bas- och en kollektorsida – en fysiskt omöjlig sak att göra, men elektriskt sett ser kretsen alla jordanslutningar som en nod, så detta påhitt är tillåtet.
Självklart gör det sätt på vilket jordledningarna är anslutna ingen skillnad för förstärkaren (de är alla en nod), men det gör en skillnad för portförhållandena. Denna konstgjordhet är en svaghet hos detta tillvägagångssätt: portförhållandena behövs för att rättfärdiga metoden, men kretsen är egentligen opåverkad av hur strömmar byts ut mellan jordförbindelserna.
Hur som helst, om inget möjligt arrangemang av jordförhållandena leder till portförhållandena, kanske kretsen inte beter sig på samma sätt. Förbättringsfaktorerna (1 + βFB AOL) för att bestämma ingångs- och utgångsimpedansen kanske inte fungerar. Denna situation är besvärlig, eftersom ett misslyckande med att göra en tvåport kan återspegla ett verkligt problem (det är helt enkelt inte möjligt), eller återspegla en brist på fantasi (t.ex. tänkte man helt enkelt inte på att dela emitternoden i två delar). När portförhållandena är tveksamma är därför minst två tillvägagångssätt möjliga för att fastställa om förbättringsfaktorerna är korrekta: antingen simulera ett exempel med Spice och jämföra resultaten med användningen av en förbättringsfaktor, eller beräkna impedansen med hjälp av en testkälla och jämföra resultaten.
Ett mer praktiskt val är att helt överge metoden med två portar och använda olika alternativ som bygger på signalflödesgrafteori, inklusive Rosenstark-metoden, Choma-metoden och användningen av Blackmans teorem. Det valet kan vara tillrådligt om modeller för enheter med små signaler är komplexa eller inte finns tillgängliga (t.ex. om enheterna endast är kända numeriskt, kanske från mätningar eller SPICE-simuleringar).