Disclaimer 1 : Den här artikeln är endast en introduktion till MFCC-funktionerna och är avsedd för dem som behöver en enkel och snabb förståelse av dem. Detaljerad matematik och invecklade detaljer diskuteras inte.
När jag aldrig själv har arbetat inom området för talbehandling, fick jag när jag hörde ordet ”MFCC” (som ofta används av mina kollegor) en otillräcklig förståelse för att det är namnet på en viss typ av ”funktion” som extraheras från ljudsignaler (i likhet med kanter som utgör en typ av funktion som extraheras från bilder).


Det krävdes en hel del läsning från flera olika källor för att jag skulle förstå vad MFCC-funktioner är. Så jag bestämde mig för att hjälpa medmänniskor i nöd genom att sammanställa den information jag samlat in på ett lättförståeligt sätt.
Låt oss börja med att expandera akronymen MFCC – Mel Frequency Cepstral Co-efficients.
Har du någonsin hört ordet cepstral förut? Förmodligen inte. Det är spektralt med omvända specifikationer! Men varför? För en mycket grundläggande förståelse är cepstrum information om förändringshastigheten i spektrala band. I den konventionella analysen av tidssignaler visas alla periodiska komponenter (t.ex. ekon) som skarpa toppar i motsvarande frekvensspektrum (dvs. Fourier-spektrum). Detta erhålls genom att tillämpa en Fouriertransform på tidssignalen). Detta kan ses i följande bild:

Om vi tar loggen av storleken på detta Fourier-spektrum och sedan återigen tar spektrumet av denna logg med hjälp av en cosinustransformation (jag vet att det låter komplicerat, men ha tålamod med mig, snälla!), observerar vi en topp överallt där det finns en periodisk komponent i den ursprungliga tidssignalen. Eftersom vi tillämpar en transformation på själva frekvensspektrumet är det resulterande spektrumet varken i frekvensdomänen eller i tidsdomänen och Bogert et al. beslöt därför att kalla det för quefrency-domänen. Och detta spektrum av loggen av tidssignalens spektrum fick namnet cepstrum (ta-da!).
Den följande bilden är en sammanfattning av de ovan förklarade stegen.

Cepstrum introducerades först för att karakterisera de seismiska ekon som uppstår på grund av jordbävningar.
Tonhöjd är en av egenskaperna för en talsignal och mäts som signalens frekvens. Melskalan är en skala som relaterar den upplevda frekvensen av en ton till den faktiska uppmätta frekvensen. Den skalar frekvensen för att bättre motsvara vad det mänskliga örat kan höra (människor är bättre på att identifiera små förändringar i tal vid lägre frekvenser). Denna skala har härletts från experiment på människor. Låt mig ge dig en intuitiv förklaring av vad mel-skalan fångar.
Det mänskliga hörselområdet är 20 Hz till 20 kHz. Föreställ dig en melodi på 300 Hz. Detta skulle låta ungefär som standardtelefontonen på en fast telefon. Föreställ dig nu en melodi på 400 Hz (en lite högre uppringningston). Jämför nu avståndet mellan dessa två, oavsett hur det uppfattas av din hjärna. Föreställ dig nu en 900 Hz-signal (som liknar ett mikrofonåterkopplingsljud) och ett 1 kHz-ljud. Det upplevda avståndet mellan dessa två ljud kan verka större än de två första, även om den faktiska skillnaden är densamma (100 Hz). Melskalan försöker fånga upp sådana skillnader. En frekvens mätt i Hertz (f) kan omvandlas till Melskalan med hjälp av följande formel :
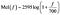
Varje ljud som alstras av människor bestäms av formen på stämbanden (inklusive tunga, tänder, etc). Om denna form kan bestämmas korrekt kan alla ljud som produceras representeras korrekt. Kuvertet i talsignalens tidseffektspektrum är representativt för stämbanden och MFCC (som inte är något annat än de koefficienter som utgör Mel-frekvenscepstrummet) representerar detta kuvert på ett korrekt sätt. Följande blockdiagram är en stegvis sammanfattning av hur vi kom fram till MFCC:
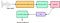
Här hänvisar Filterbank till mel-filtren (som täcker mel-skalan) och cepstralkoefficienter är inget annat än MFCC.
TL; DR – MFCC-funktioner representerar fonem (distinkta ljudenheter) eftersom formen på stämbanden (som ansvarar för ljudgenerering) är uppenbar i dem.
Disclaimer 2 : Alla bilder kommer från Google images.