- Cum a inventat un adolescent o nouă ramură a matematicii pentru a rezolva o întrebare deschisă de mult timp despre ecuații
- Rădăcinile de permutare și simetria
- Mărimea quinticului
- Câmpuri și automorfisme
- Două exemple de gradul 3
- Exemplu 2
- Grupuri
- Vizualizarea grupurilor
- Tabele Cayley
- Graficul Caylay
- Utilizări ale grupurilor
- Înapoi la domenii
- Subcâmpuri și subgrupuri
- Câmpuri fixe
- Schiță de demonstrație a teoremei fundamentale a teoriei lui Galois
- Cuantitatea
- Radicalii
- Subgrupuri ale quinticului
- Trisecția unghiului
- Rezolvarea cinticului general
Cum a inventat un adolescent o nouă ramură a matematicii pentru a rezolva o întrebare deschisă de mult timp despre ecuații

Să știți că pentru a rezolva o ecuație de gradul 2, ax²+bx+c = 0, folosim formula pătratică.
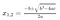
Există formule similare pentru ecuațiile de gradul 3 și 4, dar ele lipsesc în mod misterios pentru 5 sau mai mare. Mai precis, se pare că nu putem construi soluțiile quinticelor (ecuație de grad 5) sau mai mare folosind doar adunarea, scăderea, înmulțirea, împărțirea și radicalii (rădăcini pătrate, rădăcini cubice etc.). De ce se întâmplă asta, ce este atât de special la numărul 5? Acestea au fost întrebări care l-au bântuit pe tânărul francez Evariste Galois la începutul anilor 1800, iar în noaptea dinainte de a fi rănit mortal într-un duel, el a scris o teorie a unui nou obiect matematic numit „grup” care rezolvă problema într-un mod surprinzător de elegant.
Acesta este modul în care a făcut-o.
Setul rădăcinilor diferitelor ecuații este de complexitate diferită. Unele seturi sunt atât de complexe încât nu pot fi exprimate folosind doar obiecte simple, cum ar fi radicalii. Dar cum măsurăm complexitatea rădăcinilor dacă nu putem nici măcar să le calculăm și ce măsură a complexității ar trebui să folosim?
Rădăcinile de permutare și simetria
Răspunsul se află în simetria rădăcinilor.
Simetria rădăcinilor vă puteți întreba, ce legătură are asta cu ceva? Ce înseamnă măcar?
Să reprezentăm grafic rădăcinile a două ecuații și să vedem dacă putem da un sens:

Se spune că cea din stânga este mai puțin simetrică decât cea din dreapta. Acest lucru s-ar putea să vă surprindă, deoarece în sensul colocvial al cuvântului, simetric este de obicei folosit dacă se poate reflecta sau roti obiectul fără a schimba felul în care arată. În acest sens, imaginea din stânga pare mai simetrică.
De exemplu: Steaua este mai simetrică decât inima, pentru că, în afară de a o reflecta, se poate și roti.

Dar, în cazul nostru, vom avea o viziune mai generală asupra simetriilor. Nu ne limităm doar la reflexii și rotații, orice funcție care transformă obiectul fără a schimba felul în care arată este un joc corect. În cazul rădăcinilor, acest lucru înseamnă că orice funcție care schimbă (permută) rădăcinile în orice fel este valabilă. Mai multe funcții înseamnă mai simetric.
Se pare că, în cazul corect, există funcții pentru permutarea tuturor rădăcinilor în orice ordine imaginabilă, până la 5!=120, deci este foarte simetric. Dar în cazul din stânga, dacă interschimbăm r₂↔r₄ folosind transformarea i↔-i, trebuie neapărat să interschimbăm și r₁↔r₅. Acest lucru ne restrânge și, prin urmare, nu sunt posibile toate permutările imaginabile. Este mai puțin simetrică.
Funcțiile care permută rădăcinile se numesc „Automorfisme”, iar dacă grupăm aceste automorfisme împreună obținem ceea ce se numește un „Grup” (voi reveni mai târziu la definiții mai bune ale automorfismelor și grupurilor).
Aceasta înseamnă că grupul care reprezintă simetriile rădăcinilor este mai mare și mai complex în cazul corect. De fapt, grupul în cazul din dreapta este atât de complex încât rădăcinile nu pot fi descrise cu ajutorul radicalilor.
Cum știm cât de complex este un grup? Pentru a înțelege acest lucru avem nevoie de un pic mai multă teorie.
Mărimea quinticului
În primul rând, să aruncăm o privire la mărimea unui grup. De unde știu că există niște quintici care au un grup mare de 5!
Un quintic general arată în mod normal astfel:
x⁵+ax⁴+bx³+cx²+dx+e=0
Dar dacă adoptăm o abordare mai „centrată pe rădăcină” putem spune că arată astfel:
(x-r₁)(x-r₂)(x-r₃)(x-r₄)(x-r₅)=
x⁵-(r₁+r₂+r₃+r₄+r₅)x⁴+
(r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅)x³…- r₁r₂r₃r₄r₅=0
Adică, constanta a,b,c,d,e din prima ecuație se înlocuiește cu o combinație simetrică a rădăcinilor:
r₁+r₂+r₃+r₄+r₅=a
r₁r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅=b
(c și d omise pentru scurtime)
r₁r₂r₃r₄r₅ = e
Considerând în detaliu toți termenii, se descoperă că interschimbarea rădăcinilor nu afectează ecuația (încercați-o pentru b de mai sus, de exemplu). Acest lucru este valabil pentru polinoame de orice grad. Deoarece suntem capabili să interschimbăm toate rădăcinile, putem trage concluzia că grupul de simetrie pentru această quintică generală este de fapt toate permutările, numit și S₅ (grupul simetric de ordin 5).
Câmpuri și automorfisme
Acum vom extinde puțin definiția automorfismelor, deoarece acestea sunt mai mult decât simple funcții care permută rădăcinile. În acest proces trebuie să introducem ceva numit „câmpuri”. De ce am vrea să facem asta, veți spune? Motivul este că, deși este distractiv să lucrezi cu rădăcini și permutările lor, este puțin mai ușor să lucrezi cu câmpuri și automorfismele lor. Sunt exact aceleași funcții, nu vă faceți griji, doar un alt mod de a le privi.
Așa că, dacă ecuația este, să zicem x²-2=0, în loc să lucrăm cu rădăcinile, r₁=√2, r₂=-√2, vom introduce câmpul Q(√2). Acesta reprezintă toate numerele raționale Q cu un plus de √2. √2 se numește o „extensie de câmp”. Acesta arată astfel: a+b√2 a,b∈Q. Pentru a putea descrie rădăcina ecuației, avem nevoie de câmpul Q(√2). Pentru fiecare extensie de câmp (și, de asemenea, pentru alte obiecte matematice) avem o grămadă de funcții, σₙ, care trimit un număr la un alt număr unic în același câmp și respectă condiția σ(a+b)=σ(a)+σ(b) și σ(ab)=σ(a)σ(b). σ este o funcție a extensiei și nu atinge câmpul de bază Q. Aceste funcții se numesc automorfisme. Întâmplător, ele permută și rădăcinile. Acest lucru se datorează faptului că pentru rădăcina r:
r⁵+ar⁴+br³+cr²+dr+e=0⟹
σ(r⁵+ar⁴+br³+cr²+dr+e)=σ(0)⟹
σ(r)⁵+aσ(r)⁴+bσ(r)³+cσ(r)²+dσ(r)+e=0 (deoarece σ nu atinge Q (unde a, b, c, d,e trăiește))
Acest lucru înseamnă că σ(r) este, de asemenea, o soluție a ecuației. Și cum:
σ(r₁)-σ(r₂)=σ(r₁)+σ(-1)σ(r₂)=σ(r₁-r₂)≠0
rădăcinile sunt distincte, deci avem 5 dintre ele, care trebuie să fie cele 5 inițiale. Astfel, σ trebuie să permute rădăcinile.
Desigur, acest lucru funcționează pentru o ecuație de orice grad.
De aici:
- Avem ecuația noastră.
- Această ecuație are un câmp care ar putea conține o extensie de câțiva radicali
- Această extensie de câmp are un grup, care este o colecție a tuturor automorfismelor sale.
Două exemple de gradul 3
Ecuația: x³-x²-2x+2=0
Rădăcinile sunt (1,√2,-√2) (se poate verifica singur prin simpla introducere a acestora), deci câmpul trebuie să fie Q(√2)
Scriind toate modurile la care ne putem gândi pentru a permuta rădăcinile (e înseamnă permutare de identitate, nu face nimic):
(e)
(√2↔-√2)
(1↔√2)
(1↔-√2)
(√2→-√2 și 1→√2)
(√2↔-√2 și 1↔-√2)
Să testăm unul: Fie (√2↔-√2) σ₁:
σ₁(√2+-√2)=σ₁(0)=0=σ₁(√2)+σ₁(-√2)
σ₁((√2)(-√2))=σ₁(-2)=-2=σ₁(√2)σ₁(-√2)
Până aici totul este bine. Încă una.
Lasă (1↔√2) să fie σ₂:
σ₂(√2+-√2)=σ₂(0)=0 ≠ σ₂(√2)+σ₂(-√2)=1+-√2
σ₂((√2)(-√2))=2 ≠ σ₂(√2)σ₂(-√2)=1(-√2)
Se pare că σ₂ nu este un automorfism, așa că va trebui să renunțăm la el. Celelalte σ întâmpină probleme similare, singurele care rămân sunt e și σ₁. Acesta se numește grupul ciclic C₂, deoarece nu putem face permutări decât într-un cerc (un cerc foarte mic în acest caz).
Exemplu 2
Ecuația: x³-2=0
Rădăcinile sunt
atunci câmpul trebuie să fie

folosind ζ pentru a fi mai scurt. Iată cum arată:
Se poate juca puțin cu permutările rădăcinilor și se va observa curând că, în acest caz, toate sunt automorfisme. Astfel, există 3! automorfisme, care sunt toate permutările rădăcinilor, deci grupul trebuie să fie S₃.
Un alt lucru amuzant de observat în legătură cu imaginea de mai sus este că aceasta arată ca un triunghi echilateral și că automorfismele corespund exact rotirii și reflectării triunghiului. Dacă automorfismele corespund simetriilor unui poligon regulat în acest fel, grupul se numește „grup diedru”. În acest caz, D₃. De obicei, grupul tuturor permutărilor Sₙ nu este același cu grupul diedru Dₙ, dar în cazul n=3 este.
Grupuri
Acesta pare a fi un loc bun pentru a trece la o discuție ceva mai lungă despre grupuri. Așadar, grupurile au început ca fiind colecții de permutări de rădăcini, dar pot fi văzute și ca colecții de automorfisme, sau rotații și reflexii ale obiectelor geometrice simetrice. Orice colecție de funcții care modifică un obiect în așa fel încât acesta să arate la fel poate fi considerată un grup. Dar, de fapt, ne putem uita la transformările în sine fără a ne preocupa de obiectul simetric asupra căruia acționează. În același mod în care nu ne deranjăm de grămezile de mere atunci când facem aritmetică, ci pur și simplu urmăm regulile, în mod similar putem defini niște reguli pe care le urmează transformările unui grup și le putem folosi.
Regulile sunt cam așa:
Dacă facem mai întâi o transformare și apoi încă una, vom obține o a treia transformare care este tot în grup. De exemplu, grupul C₄ este grupul tuturor rotațiilor care se pot face pe un pătrat. Dacă a se rotește la 90∘, b se rotește la 180∘ și c se rotește la 270∘, atunci a∗b=c. Unde ∗ înseamnă că mai întâi se face b, apoi a, ceea ce se numește în mod obișnuit înmulțire, deoarece este (oarecum) similar cu înmulțirea numerelor. Conform regulii de mai sus, c trebuie să fie în grup. Aceasta se numește închidere.
Trebuie să existe un element de identitate (e) care nu face absolut nimic.
Pentru fiecare element trebuie să existe un invers al acelui element.
Acum, putem investiga caracteristicile diferitelor grupuri fără a trebui să ne facem griji cu privire la rădăcini sau poligoane.
Vizualizarea grupurilor
Două moduri amuzante de a vizualiza grupurile sunt:
Tabele Cayley
Tabela Caylay de mai sus este tabelul Caylay pentru un triunghi echilateral, grupul D₃. Sunt toate elementele grupului și ce elemente obținem atunci când le înmulțim. De exemplu, dacă facem mai întâi o rotație de 120∘ (r) și apoi aceeași rotație din nou, obținem o rotație de 240∘ rr=r², după cum se poate vedea în tabel. Dacă facem o rotație de 120∘ rotație-întoarcere rf și o r ajungem să avem doar o întoarcere. Observați cum elementele f și r nu se comută. Un grup în care elementele se comută se numește grup abelian.
Acest tabel particular este totuși foarte simetric, dar nu este necesar să fie așa. Orice amestecare a elementelor care respectă regulile este valabilă.
Graficul Caylay
Graficul de mai sus este graficul D₃ Caylay. Aici elementele sunt afișate într-un mod care să arate cum se ajunge de la un element la altul, unde marginile reprezintă operațiile. În acest caz este necesară o rotație de 120∘ și o răsturnare, acestea (r și f) se mai numesc și generatoare ale grupului, deoarece se poate genera întregul grup cu ele, pornind de la elementul identitate.
Utilizări ale grupurilor

Grupurile tind să fie utile peste tot unde există simetrie. De exemplu, grupurile de tapet sunt folosite pentru a descrie tapeturile simetrice. Există unele imagini de fundal care pot fi rotite cu 180∘ și unele imagini de fundal care pot fi reflectate și unele în care le putem face pe amândouă, și așa mai departe. Se pare că există doar 17 dintre ele, așa că este un mod îngrijit de clasificare a imaginilor de fundal.
Ambele imagini de fundal de mai sus aparțin amândouă unui grup numit p6m.
O altă utilizare, mai surprinzătoare, a grupurilor este în fizică. Se pare că legile naturii urmează anumite simetrii. De exemplu, dacă se transformă a doua lege a lui Newtons, F=ma, 10 minute în viitor este tot aceeași. Faptul că legile naturii nu se schimbă de la o zi la alta pare să indice că acestea sunt simetrice în ceea ce privește transformarea în timp. De asemenea, ele nu se schimbă nici de la un loc la altul, astfel încât sunt permise și transformările în spațiu. Deoarece este posibilă transformarea timpului și a spațiului în bucăți arbitrar de mici sau mari, grupurile care le descriu, grupurile Lie, conțin o cantitate infinită de elemente.
Interesant este faptul că toate aceste simetrii sunt legate de câte o lege de conservare. Simetria temporală presupune conservarea energiei, simetria spațială conservarea momentului, simetria unghiulară (natura arată la fel din toate unghiurile) conservarea momentului unghiular și așa mai departe. Acest lucru a fost demonstrat de Emmy Noether prin simpla combinare a simetriilor cu principiul celei mai mici acțiuni, o lege a naturii care afirmă că natura tinde să „urmeze calea cea mai scurtă”.
Constat că este interesant cât de mult din toată complexitatea și aparentul haos al naturii poate fi explicat prin concepte intuitive precum „legile naturii nu se schimbă de la o zi la alta” și „natura tinde să urmeze calea cea mai scurtă”.
Înapoi la domenii
Sfârșitul intermezzo-ului, unde rămăsesem? Corect, vorbeam despre x³-3=0 și despre rădăcinile și câmpurile sale.
Câmpului acestei ecuații este Q(³√2, ζ) și ar fi firesc să credem că arată astfel: a+b³√2+cζ, dar este greșit. Motivul este că dorim ca câmpul nostru să fie „închis”. Adică, dacă adăugăm sau înmulțim două elemente din câmp, dorim să rămână în câmp. Astfel, de exemplu, ³√2 și ζ sunt ambele în câmpul de mai sus, dar ³√2ζ nu este.

Subcâmpuri și subgrupuri
Cu privire la exemplele noastre de gradul 3 de mai sus avem
.
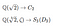
S-ar părea că al doilea câmp și al doilea grup sunt mai complexe decât primul câmp și primul grup. Putem ghici acest lucru prin simpla numărare a numărului de termeni în cazul câmpului sau a numărului de automorfisme în cazul grupului. Dar simpla numărare nu pare să surprindă cu adevărat ceea ce înseamnă să fii complex. Să luăm, de exemplu, grupul C₁₂. O mulțime de elemente, dar nu face decât să rotească rădăcinile, așa că nu pare chiar atât de complex. Un câmp corespunzător este Q(e^π/6). Acesta va conține e^π/6,e^2π/6… dar, din nou, nu este foarte complex.
Îngrijorarea cu privire la cât de complex este un grup va fi esențială pentru a înțelege de ce unele rădăcini nu pot fi descrise doar prin radicali, țineți minte.
Pentru a avea o modalitate mai bună de a aprecia complexitatea, vom introduce conceptul de „Subcâmp” și „Subgrup”. Un subcâmp este atunci când îndepărtați o parte din termeni, dar aveți în continuare un câmp închis. În mod similar, un subgrup este atunci când eliminați unele dintre automorfisme, dar aveți în continuare un grup închis.
În primul caz Q(√2), singurul lucru pe care îl putem face este să eliminăm √2 din câmp și unul dintre cele două automorfisme din grup (nu putem elimina (e) și să avem în continuare un grup).
În ceea ce privește al doilea caz Q(³√2, ζ), situația devine puțin mai complicată. Se poate distila manual subcâmpurile/grupurile prin simpla eliminare a unor elemente, unul câte unul, și se poate vedea dacă câmpul/grupul rezultat este închis. După un timp ajungem la aceasta:
Interesant, atât câmpul cât și grupul au patru constituenți. Acum, ar fi o presupunere rezonabilă că subgrupurile conțin întotdeauna exact automorfismele subcâmpurilor. Dar nu este așa.
Câmpuri fixe
Nu vă faceți griji, aproape am ajuns, este doar un pic mai complicat. Pentru a vedea acest lucru, să ne uităm la câmpul Q(⁴√2, i) și la subcâmpurile sale.
Câmpului Q(⁴√2, i) îi corespunde grupul de permutare D₄ (același cu cel al unui pătrat). Să ne uităm la D₄ și la subgrupurile sale.
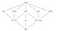
Rețeaua subgrupurilor este cu susul în jos în această imagine, cu D₄ în partea de jos, voi ajunge la asta în scurt timp, dar să ne uităm mai întâi la subcâmpurile contra subgrupurilor. Q(⁴√2, i) are 5 subcâmpuri mari și 3 subcâmpuri mici, dar D₄ are doar 3 subgrupuri mari și 5 subgrupuri mai mici.
S-ar părea că nu există suficiente grupuri mari pentru a permuta cele 5 câmpuri mari. Dacă v-ați juca cu subgrupurile și subcâmpurile, ați ajunge în cele din urmă la concluzia că subgrupurile permută de fapt nu subcâmpurile, ci mai degrabă tot ceea ce nu se află în subcâmpuri, că ele „repară” sau nu se ating de subcâmpuri.
Așa că, de exemplu, (f) fixează Q(⁴√2) și (r², f) fixează Q(√2).
De ce este așa și nu invers, așa cum am presupus la început?
Nu am un mod intuitiv de a explica acest lucru, modul în care văd eu lucrurile este că am descoperit-o empiric și acum putem încerca să o demonstrăm. Demonstrația sună cam așa:
Schiță de demonstrație a teoremei fundamentale a teoriei lui Galois
Vrem să arătăm că dacă întoarcem cu susul în jos rețeaua de subgrupuri obținem o corespondență biunivocă cu rețeaua de subcâmpuri în care câmpurile sunt câmpurile fixe ale grupurilor.
În primul rând, aș vrea să subliniez că este rezonabil (oarecum) ca acest lucru să se întâmple. La grupul de jos, avem toate automorfismele, care, desigur, se deplasează în jurul a tot, cu excepția lui Q (fixează Q), iar în partea de sus, avem doar e-automorfismul, care nu se deplasează în jurul a nimic (fixează totul).
Dacă începem de la grupul de jos și eliminăm câteva dintre automorfisme, automorfismele eliminate nu se vor mai deplasa în jurul unei mici părți a câmpului și astfel vor fixa acea parte a câmpului. Pe măsură ce eliminăm mai multe automorfisme, o parte din ce în ce mai mare a câmpului nu va fi afectată și astfel vom avea un câmp fix mai mare.
Pentru a fi un pic mai riguroși, va trebui să putem compara mărimea grupului și a câmpului. Mărimea grupului este, bineînțeles, numărul de automorfisme din el. Mărimea câmpului este numărul de termeni. Se întâmplă ca acestea două să fie identice, dar de ce se întâmplă acest lucru?

Cuantitatea
Acum, am putea să ne uităm la rețeaua de subgrupuri S₅ a quinticului și să vedem că, într-adevăr, aceasta pare destul de complexă. Dar, pentru a lega acest lucru de radicali, avem nevoie de o modalitate de a analiza complexitatea între grupuri și subgrupurile sale. Adică: Cât de mult mai complex este D₄ decât C₄, de exemplu? Pentru a face acest lucru, introducem conceptul de „coeficient”. Un coeficient este, practic, o diviziune de grup. Cum funcționează asta?
În diviziunea obișnuită facem ceva de genul acesta: Pentru a împărți 15 mere pe 5 persoane, grupăm merele din setul de mere în 5 grămezi egale și fiecare grămadă va corespunde unei persoane din setul de persoane. Răspunsul la întrebarea 15/5 este 3, una dintre grămezi, orice grămadă este suficientă, deoarece sunt egale.
Un lucru similar se întâmplă atunci când împărțim grupuri. Pentru a împărți D₄ la C₄, grupăm cele 8 elemente din D₄ în 4 grupe egale, câte una pentru fiecare element din C₄. Cum facem ca grupurile să fie egale? Nu este ca și cum elementele ar fi toate mere identice. Ele pot fi automorfisme foarte diferite, de exemplu. Ei bine, cvorumurile nu sunt întotdeauna posibile exact din acest motiv. Dar, uneori, un grup poate fi împărțit în „Coseturi”. Să zicem că împărțim D₄ în 4 părți egale cu câte 2 elemente în fiecare. Dacă suntem norocoși, putem avea 4 grămezi de elemente în care relația dintre cele două elemente este aceeași în toate grămezile. Pentru a putea face acest lucru, grupul inițial trebuie să prezinte un nivel ridicat de auto-similitudine. Pentru a vedea acest lucru, să ne uităm la un grafic Cayley al lui D₄.
După cum se poate vedea, există de fapt un nivel ridicat de auto-similitudine aici. Colțul din stânga sus, cel din dreapta sus, cel din stânga jos și cel din dreapta jos arată la fel. Acesta este cosetul nostru.
Atunci D₄/C₄ este practic unul dintre aceste coseturi, care este C₂. Așadar: D₄/C₄=C₂.
Acum, prin introducerea cuantelor, avem de fapt un concept despre cum să construim grupuri de la zero. Așa cum 21 este format din 3 și 7, tot așa și grupurile sunt formate din subgrupurile lor. Și așa cum putem obține constituenții unui număr prin împărțire, 21/7=3, tot așa putem obține constituenții unui grup luând cutientul. Deoarece D₄/C₄=C₂, aceasta înseamnă că, dacă avem un grup C₄, trebuie să îl înmulțim cu C₂ pentru a ajunge la D₄. Deoarece există o corespondență între câmpuri și grupuri, acest lucru va juca un rol în modul în care construim câmpurile.
Radicalii

Subgrupuri ale quinticului
Acum, Nu voi arăta o imagine a rețelei de grupuri a lui S₅ pentru că este prea mare, dar voi spune câteva lucruri despre subgrupurile sale. Unul dintre subgrupuri este A₅ (grup alternativ), ceea ce este ușor de verificat. Pentru a ajunge de la A₅ la S₅ avem nevoie de S₅/A₅=C₂. Astfel, putem ajunge acolo prin radicali, dar: Un subgrup din A₅ este (e), dar A₅/e nu este un grup ciclic. Apropo, acest lucru este valabil pentru orice An cu n≥5. Așadar, nu putem ajunge acolo prin radicali și, din păcate, orice polinom de grad≥5 nu poate fi rezolvat prin radicali.
Și iată cum Galois, pe când era adolescent, a inventat conceptul de grup pentru a demonstra o întrebare deschisă de mult timp cu privire la nerezolvabilitatea quinticului⁹.
Trisecția unghiului
Un fapt bonus amuzant pe care îl obținem din mașinăria care înconjoară teoria lui Galois, în acest caz legea turnului pentru câmpuri, este o dovadă frumoasă a unei probleme care a pus în încurcătură omenirea încă de la grecii antici, și anume: imposibilitatea de a trisecta un unghi cu o dreaptă și un compas. Se pare că grecilor le plăcea să deseneze lucruri în acest mod și erau curioși în legătură cu limitele metodei.
Un exemplu este găsirea unui punct în mijlocul altor două puncte. Pentru a face acest lucru, se fixează compasul pe cele două puncte și se desenează mai întâi un cerc în jurul unuia și apoi în jurul celuilalt. Folosiți rigla pe post de riglă și trageți o linie între cele două puncte și apoi între punctele în care se intersectează cercurile. Mijlocul este locul unde se intersectează liniile.
Dar cum se transpune acest mod de a desena în teoria câmpului? Ei bine, se poate vedea problema de mai sus ca, să zicem că avem un câmp format din două puncte, (x₁,y₁) și (x₂,y₂). Am dori să extindem câmpul pentru a conține și punctul din mijloc. Pentru a face acest lucru, vom găsi intersecțiile cercurilor (x-x₁)²+(y-y₁)²=r și (x-x₂)²+(y-y₂)²=r. Se obțin două noi puncte (x₃, y₃) și (x₄,y₄). Dreapta dintre ele este y=(y₄-y₃)/(x₄-x₃)x. Dreapta dintre primele două puncte este y=(y₂-y₁)/(x₂-x₁)x. Rezolvați pentru x pentru a obține locul unde ele se intersectează.
Aproape, construcțiile cu rigla și compasul echivalează cu rezolvarea unor ecuații de gradul unu și doi.
Dar la ce echivalează trisecția unui unghi?
Formula triplului unghiului dă:

Dar din moment ce folosirea riglei și compasului echivalează cu rezolvarea unor ecuații de unu și două dimensiuni, singurele extinderi de câmp posibile sunt 2 pentru o operație, iar apoi folosind noile puncte putem ajunge la puteri de 2: 4,8,16 etc. dar niciodată 3.
Deși este imposibilă trisecția unghiului folosind doar rigla și compasul este posibilă folosind origami.
Rezolvarea cinticului general
Trebuie spus că, deși cinticul general nu poate fi rezolvat cu ajutorul radicalilor, el poate fi rezolvat cu ajutorul „funcției teta Jacobi”.
- Teoria galois pentru începători: O perspectivă istorică. Jörg Bewersdorff
- http://pi.math.cornell.edu/~kbro…
- Automorfisme de câmp
- https://kconrad.math.uconn.edu/b…
- https://faculty.math.illinois.ed…
- Wolfram|Alpha: Făcând calculabilă cunoașterea lumii
- https://www.wikiwand.com/en/Galois_theory
- https://www.wikiwand.com/en/%C3%89variste_Galois
- https://www.youtube.com/watch?v=8qkfW35AqrQ&list=PLwV-9DG53NDxU337smpTwm6sef4x-SCLv&index=36