În tutorialul privind modelele liniare generalizate, am învățat despre diferite GLM-uri, cum ar fi regresia liniară, regresia logistică, etc.. În acest tutorial din seria de tutoriale R de la TechVidvan’s R, vom examina în detaliu regresia liniară în R. Vom învăța ce este regresia liniară în R și cum să o implementăm în R. Vom analiza metoda de estimare a celui mai mic pătrat și vom învăța, de asemenea, cum să verificăm acuratețea modelului.

Deci, fără alte comentarii, să începem!

Regresie liniară în R

Regresia liniară în R este o metodă utilizată pentru a prezice valoarea unei variabile folosind valoarea (valorile) uneia sau mai multor variabile predictive de intrare. Scopul regresiei liniare este de a stabili o relație liniară între variabila de ieșire dorită și predictorii de intrare.

Pentru a modela o variabilă continuă Y ca o funcție a uneia sau mai multor variabile predictoare de intrare Xi, astfel încât funcția să poată fi utilizată pentru a prezice valoarea lui Y atunci când sunt cunoscute doar valorile lui Xi. Forma generală a unei astfel de relații liniare este:

Y=?0+?1 X

Aici, ?0 este intercepția
și ?1 este panta.

Tipuri de regresie liniară în R

Există două tipuri de regresie liniară în R:

• Regresie liniară simplă
• Regresie liniară multiplă

Să ne uităm la acestea una câte una.

Simple Linear Regression in R

Regresia liniară simplă are ca scop găsirea unei relații liniare între două variabile continue. Este important de reținut că relația este de natură statistică și nu deterministă.

O relație deterministă este una în care valoarea unei variabile poate fi găsită cu precizie prin utilizarea valorii celeilalte variabile. Un exemplu de relație deterministă este cea dintre kilometri și mile. Folosind valoarea kilometrului, putem afla cu precizie distanța în mile. O relație statistică nu este precisă și are întotdeauna o eroare de predicție. De exemplu, având suficiente date, putem găsi o relație între înălțimea și greutatea unei persoane, dar va exista întotdeauna o marjă de eroare și vor exista cazuri excepționale.

Ideea din spatele regresiei liniare simple este de a găsi o dreaptă care se potrivește cel mai bine cu valorile date ale celor două variabile. Această linie ne poate ajuta apoi să găsim valorile variabilei dependente atunci când acestea lipsesc.

Să studiem acest lucru cu ajutorul unui exemplu. Avem un set de date format din înălțimile și greutățile a 500 de persoane. Scopul nostru aici este de a construi un model de regresie liniară care să formuleze relația dintre înălțime și greutate, astfel încât atunci când dăm înălțimea (Y) ca intrare în model, acesta să ne poată da în schimb greutatea (X) cu o marjă sau eroare minimă.

Y=b0+b1X

Valorile lui b0 și b1 ar trebui să fie alese astfel încât să minimizeze marja de eroare. Metrica de eroare poate fi utilizată pentru a măsura acuratețea modelului.

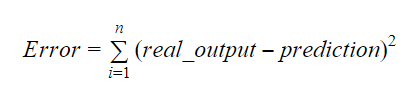
Puteți calcula panta sau coeficientul ca: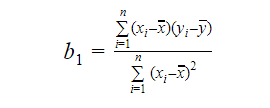

Valoarea lui b1 ne oferă o perspectivă asupra naturii relației dintre variabilele dependente și independente.

• Dacă b1 > 0, atunci variabilele au o relație pozitivă, adică. creșterea lui x va duce la o creștere a lui y.
• Dacă b1 < 0, atunci variabilele au o relație negativă, adică creșterea lui x va duce la o scădere a lui y.

Valoarea lui b0 sau intercepția poate fi calculată după cum urmează: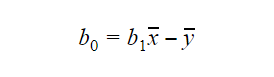
Valoarea lui b0 poate oferi, de asemenea, multe informații despre model și viceversa.

Dacă modelul nu include x=0, atunci predicția este lipsită de sens fără b1. Pentru ca modelul să aibă doar b0 și nu b1 în el în orice punct, valoarea lui x trebuie să fie 0 în acel punct. În cazuri precum cel al înălțimii, x nu poate fi 0, iar înălțimea unei persoane nu poate fi 0. Prin urmare, un astfel de model este lipsit de sens doar cu b0.

Dacă lipsește termenul b0, atunci modelul va trece prin origine, ceea ce va însemna că predicția și coeficientul de regresie (panta) vor fi distorsionate.

Regresie liniară multiplă în R

Regresia liniară multiplă este o extensie a regresiei liniare simple. În regresia liniară multiplă, urmărim să creăm un model liniar care poate prezice valoarea variabilei țintă folosind valorile mai multor variabile predictive. Forma generală a unei astfel de funcții este următoarea:

Y=b0+b1X1+b2X2+…+bnXn

Evaluarea acurateței modelului

Există diverse metode de evaluare a calității și acurateței modelului. Să analizăm pe rând câteva dintre aceste metode.

R-Squared

Informația reală din date este varianța vehiculată în ele. R-pătrat ne spune care este proporția de variație în variabila țintă (y) explicată de model. Putem găsi măsura R pătrat a unui model folosind următoarea formulă: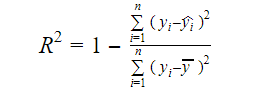

Unde,

• yi este valoarea ajustată a lui y pentru observația i
• y este media lui Y.

O valoare mai mică a lui R pătrat semnifică o acuratețe mai mică a modelului. Cu toate acestea, măsura R pătrat nu este neapărat un factor decisiv final.

R pătrat ajustat

Cu cât crește numărul de variabile în model, crește și valoarea R pătrat. Acest lucru provoacă, de asemenea, erori în variația explicată de variabilele nou adăugate. Prin urmare, ajustăm formula pentru R pătrat pentru variabile multiple.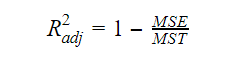
Aici, MSE reprezintă Eroarea standard medie care este:

Și MST reprezintă Totalul standard mediu care este dat de: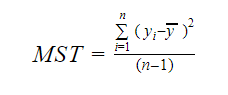

Unde, n este numărul de observații și q este numărul de coeficienți.

Relația dintre R pătrat și R pătrat ajustat este: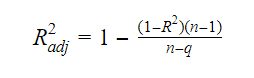

Eroarea standard și statistica F

Eroarea standard și statistica F sunt amândouă măsuri ale calității de potrivire a unui model. Formulele pentru eroarea standard și F-statistică sunt:

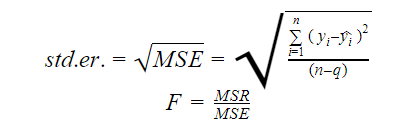
Unde MSR înseamnă Mean Square Regression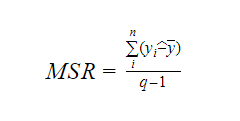

AIC și BIC

Criteriul informațional al lui Akaike și criteriul informațional bayesian sunt măsuri ale calității de potrivire a modelelor statistice. Ele pot fi, de asemenea, utilizate ca și criterii pentru selectarea unui model.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Unde,

• L este funcția de verosimilitate,
• k este numărul de parametri ai modelului,
• n este dimensiunea eșantionului.

Funcția lm în R

Funcția lm() din R ajustează modelele liniare. Ea poate efectua regresia și analiza varianței și a covarianței. Sintaxa funcției lm este următoarea:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Unde,

• formula este un obiect din clasa „formula” și este o reprezentare simbolică a modelului care urmează să se potrivească,
• date este cadrul de date sau lista care conține variabilele din formulă(date este un argument opțional. Dacă lipsește, funcția preia variabilele din mediul înconjurător),
• subset este un vector opțional care conține un subset de observații care urmează să fie utilizate în procesul de ajustare,
• weights este un vector opțional care specifică ponderile care urmează să fie utilizate în procesul de ajustare,
• na.action este o funcție care arată ce ar trebui să se întâmple atunci când se întâlnesc NA-uri în date,
• method semnifică metoda de ajustare a modelului,
• model, x, y și qr sunt logici care controlează dacă valorile corespunzătoare ar trebui să fie returnate sau nu împreună cu ieșirea. Aceste valori sunt:
• model: cadrul modelului
• x: matricea modelului
• y: răspunsul
• qr: descompunerea qr
• singular.ok este un logic care controlează dacă sunt permise sau nu ajustările singulare,
• offset este un predictor cunoscut în prealabil care ar trebui să fie utilizat în model,
• . . . . sunt argumente suplimentare care trebuie transmise funcțiilor de regresie de nivel inferior.

Exemplu practic de regresie liniară în R

Aceasta este suficientă teorie pentru moment. Să aruncăm o privire asupra modului de implementare a tuturor acestor lucruri. Vom ajusta un model liniar folosind regresia liniară în R cu ajutorul funcției lm(). Vom verifica, de asemenea, calitatea de potrivire a modelului după aceea. Să folosim setul de date autoturisme, care este furnizat în mod implicit în pachetul de bază R.

1. Să începem cu o analiză grafică a setului de date pentru a ne familiariza mai bine cu acesta. Pentru a face acest lucru, vom desena un grafic de dispersie și vom verifica ce ne spune acesta despre date.

Potem folosi funcția scatter.smooth() pentru a crea un grafic de dispersie pentru setul de date.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Succes

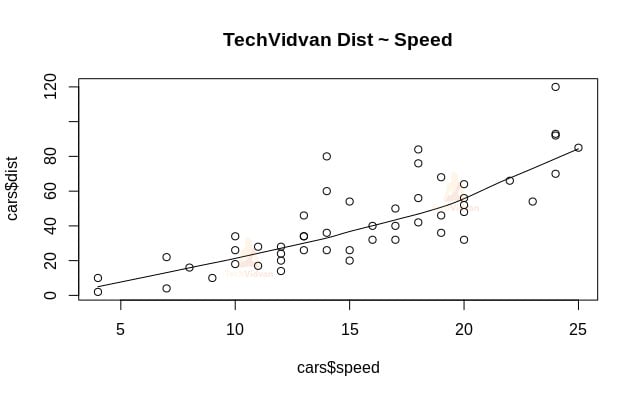
Graficul de dispersie ne arată o corelație pozitivă între distanță și viteză. Aceasta sugerează o relație liniar crescătoare între cele două variabile. Acest lucru face ca datele să fie potrivite pentru regresia liniară, deoarece o relație liniară este o ipoteză de bază pentru ajustarea unui model liniar pe date.

2. Acum că am verificat că regresia liniară este potrivită pentru date, putem folosi funcția lm() pentru a le ajusta un model liniar.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Salire

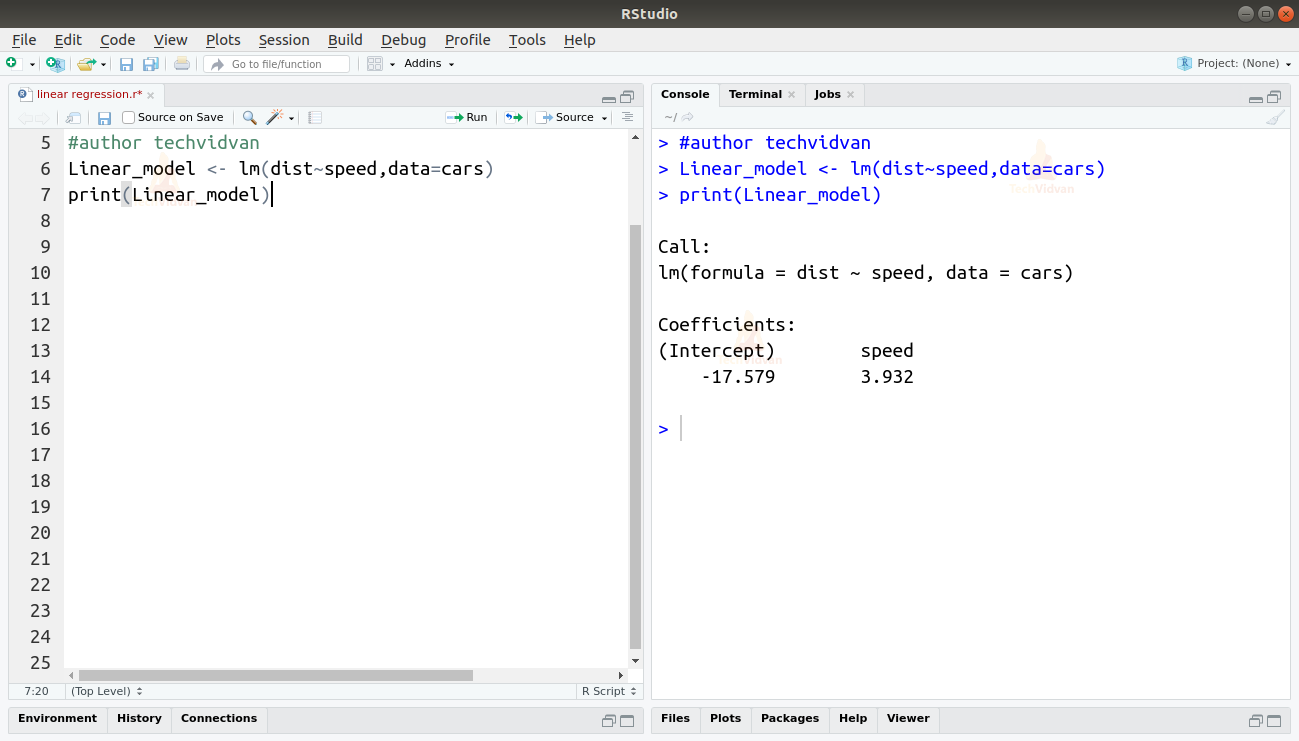
Salirea funcției lm() ne arată intercepția și coeficientul de viteză. Astfel, definim relația liniară dintre distanță și viteză ca fiind:

Distanță=Intercept+coeficient*viteză

Distanța=-17,579+3,932*viteză

3. Acum că am ajustat un model, să verificăm calitatea sau bonitatea ajustării. Să începem prin a verifica rezumatul modelului liniar cu ajutorul funcției summary().

summary(Linear_model)

Output

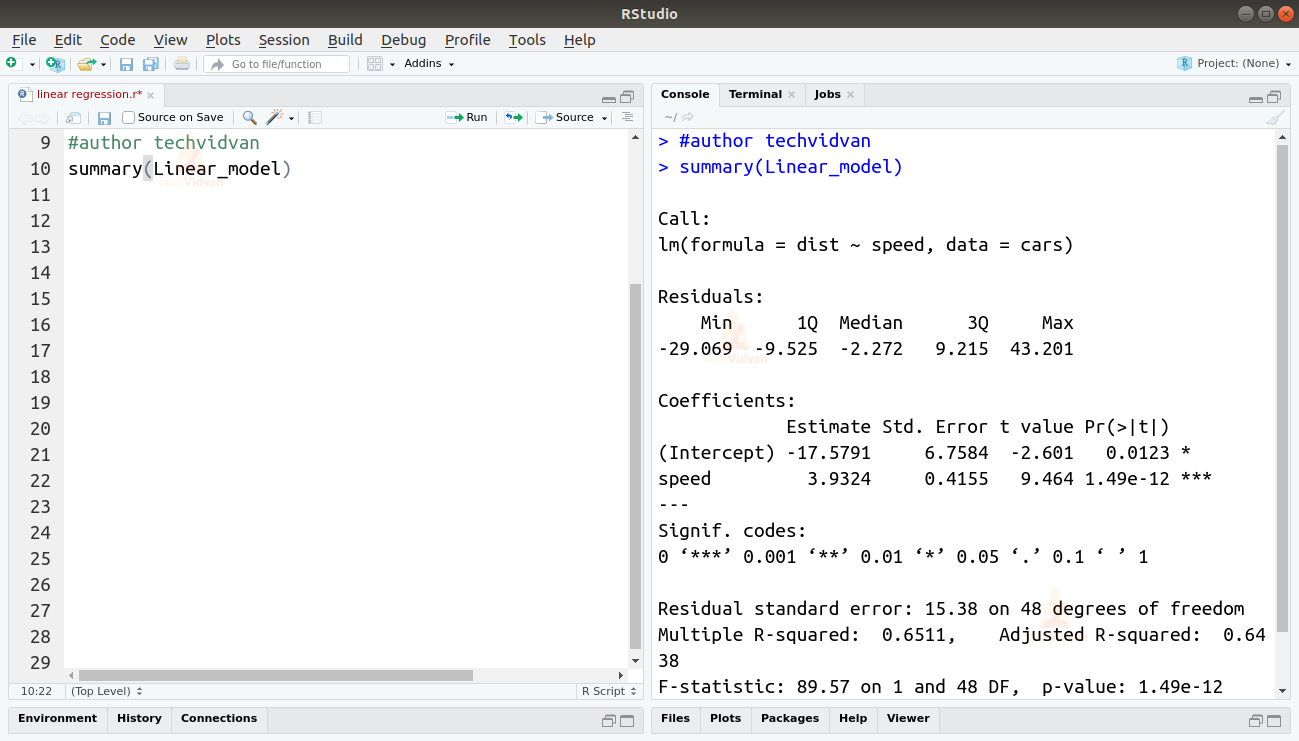
Funcția summary() ne oferă câteva măsuri importante pentru a ne ajuta să diagnosticăm ajustarea modelului. Valoarea p este o măsură importantă a gradului de adecvare a unui model. Se spune că un model nu se potrivește dacă valoarea p este mai mare decât un nivel de semnificație statistică predeterminat, care este, în mod ideal, de 0,05.

Sinteza ne oferă, de asemenea, valoarea t. Cu cât valoarea t este mai mare, cu atât mai bine se potrivește modelul.
De asemenea, putem afla AIC și BIC folosind funcțiile AIC() și BIC().

AIC(Linear_model)BIC(Linear_model)

Output

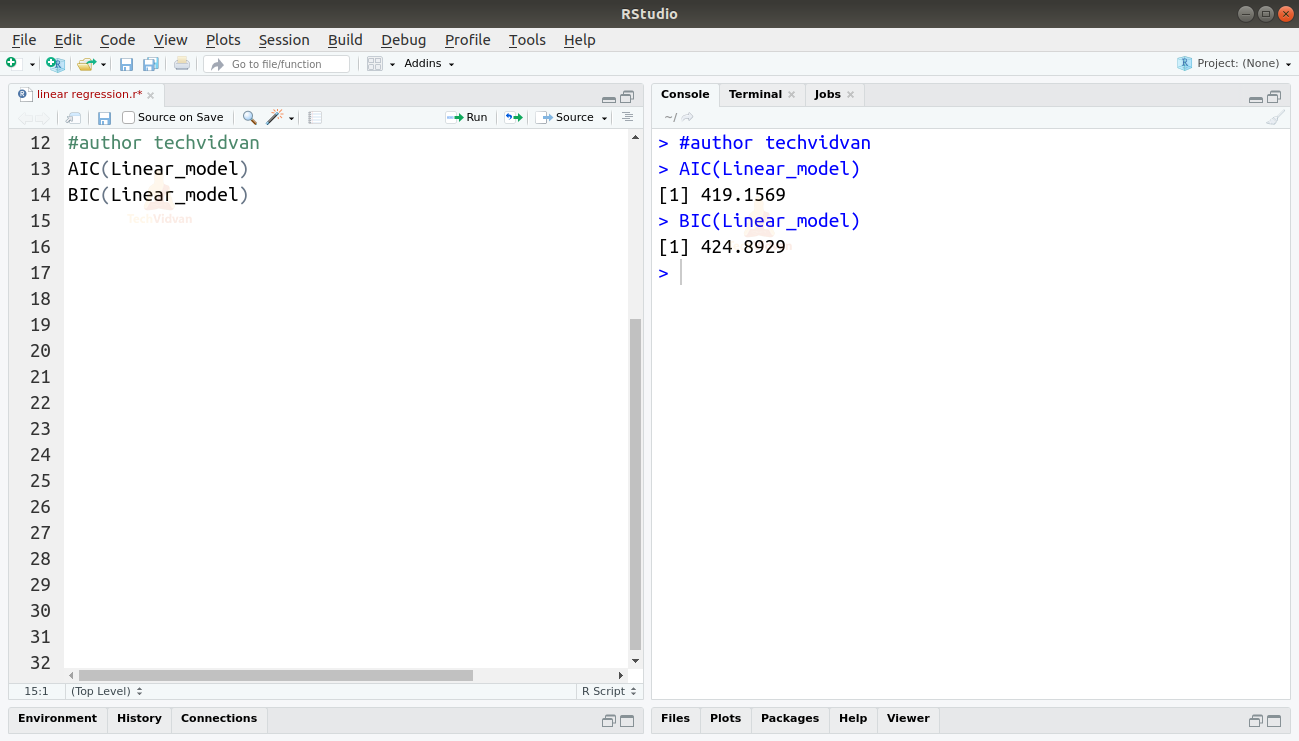
Modelul care rezultă în cele mai mici scoruri AIC și BIC este cel mai preferat.

Summary

În acest capitol din seria de tutoriale R de la TechVidvan’s R, am învățat despre regresia liniară. Am învățat despre regresia liniară simplă și regresia liniară multiplă. Apoi am studiat diverse măsuri pentru a evalua calitatea sau acuratețea modelului, cum ar fi R2, R2 ajustat, eroarea standard, F-statistica, AIC și BIC. Apoi am învățat cum să implementăm regresia liniară în R. Am verificat apoi calitatea potrivirii modelului în R.

Dați share rating-ul pe Google dacă v-a plăcut tutorialul Regresie liniară.

.