Un metamaterial electromagnetic afectează undele electromagnetice care se lovesc sau interacționează cu caracteristicile sale structurale, care sunt mai mici decât lungimea de undă. Pentru a se comporta ca un material omogen descris cu exactitate de un indice de refracție efectiv, caracteristicile sale trebuie să fie mult mai mici decât lungimea de undă.

Pentru radiația de microunde, caracteristicile sunt de ordinul milimetrilor. Metamaterialele pentru frecvențe de microunde sunt de obicei construite ca rețele de elemente conductoare de electricitate (cum ar fi buclele de sârmă) care au caracteristici inductive și capacitive adecvate. Multe metamateriale de microunde utilizează rezonatoare cu inel divizat.

Metamaterialele fotonice sunt structurate la scară nanometrică și manipulează lumina la frecvențe optice. Cristalele fotonice și suprafețele selective în funcție de frecvență, cum ar fi rețelele de difracție, oglinzile dielectrice și straturile optice, prezintă asemănări cu metamaterialele structurate pe sub lungimea de undă. Cu toate acestea, acestea sunt de obicei considerate distincte de metamateriale, deoarece funcția lor rezultă din difracție sau interferență și, prin urmare, nu pot fi aproximate ca un material omogen. Cu toate acestea, structurile materiale, cum ar fi cristalele fotonice, sunt eficiente în spectrul luminii vizibile. Mijlocul spectrului vizibil are o lungime de undă de aproximativ 560 nm (pentru lumina solară). Structurile de cristale fotonice au, în general, jumătate din această dimensiune sau mai mici, adică <280 nm.

Metamaterialele plasmonice utilizează plasmoni de suprafață, care sunt pachete de sarcină electrică ce oscilează colectiv la suprafețele metalelor la frecvențe optice.

Suprafețele selective de frecvență (FSS) pot prezenta caracteristici sub lungimea de undă și sunt cunoscute în mod diferit ca și conductori magnetici artificiali (AMC) sau suprafețe de înaltă impedanță (HIS). FSS prezintă caracteristici inductive și capacitive care sunt direct legate de structura lor sub-lungime de undă.

Metamaterialele electromagnetice pot fi împărțite în diferite clase, după cum urmează:

Indice de refracție negativEdit

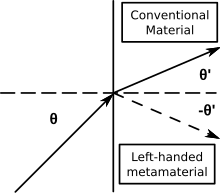
Metamaterialele cu indice negativ (NIM) sunt caracterizate de un indice de refracție negativ. Alți termeni pentru NIM-uri includ „medii stângace”, „medii cu indice de refracție negativ” și „medii cu undă inversă”. NIM-urile în care indicele de refracție negativ provine simultan din permitivitatea negativă și permeabilitatea negativă sunt, de asemenea, cunoscute sub numele de metamateriale dublu negative sau materiale dublu negative (DNG).

Să presupunem un material bine aproximat cu o permitivitate și o permeabilitate reale, relația dintre permitivitatea ϵ r {\displaystyle \epsilon _{r}}

, permeabilitatea μ r {\displaystyle \mu _{r}}

și indicele de refracție n este dat de n = ± ϵ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{\mathrm {r} }\mu _{\mathrm {r} }}}}

. Toate materialele transparente non-metamateriale cunoscute (sticlă, apă, …) posedă ϵ r {\displaystyle \epsilon _{r}} pozitiv.

și μ r {\displaystyle \mu _{r}}}

. Prin convenție, pentru n se folosește rădăcina pătrată pozitivă. Cu toate acestea, unele metamateriale proiectate au ϵ r {\displaystyle \epsilon _{r}}.

și μ r < 0 {\displaystyle \mu _{r}<0}

. Deoarece produsul ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}}}.

este pozitiv, n este real. În aceste condiții, este necesar să se ia rădăcina pătrată negativă pentru n. Atunci când atât ϵ r {\displaystyle \epsilon _{r}}

și μ r {\displaystyle \mu _{r}}

sunt pozitive (negative), undele se deplasează în direcția înainte (înapoi). Undele electromagnetice nu se pot propaga în materiale cu ϵ r {\displaystyle \epsilon _{r}}.

și μ r {\displaystyle \mu _{r}}

de semn opus pe măsură ce indicele de refracție devine imaginar. Astfel de materiale sunt opace pentru radiația electromagnetică și printre exemple se numără materialele plasmonice, cum ar fi metalele (aur, argint, …).

Considerările de mai sus sunt simpliste pentru materialele reale, care trebuie să aibă valoarea complexă ϵ r {\displaystyle \epsilon _{r}}.

și μ r {\displaystyle \mu _{r}}

. Părțile reale ale ambelor ϵ r {\displaystyle \epsilon _{r}}

și μ r {\displaystyle \mu _{r}}

nu trebuie să fie negative pentru ca un material pasiv să prezinte refracție negativă. Într-adevăr, un indice de refracție negativ pentru undele polarizate circular poate apărea și din cauza chiralității. Metamaterialele cu n negativ au numeroase proprietăți interesante:

• Legea lui Snell (n1sinθ1 = n2sinθ2) descrie în continuare refracția, dar cum n2 este negativ, razele incidente și cele refractate se află de aceeași parte a normalei la suprafață la o interfață de materiale cu indice pozitiv și negativ.
• Radiația Cherenkov indică în direcția opusă.
• Vectoriul Poynting mediat în timp este antiparalel cu viteza de fază. Cu toate acestea, pentru ca undele (energia) să se propage, un -µ trebuie să fie împerecheat cu un -ε pentru a satisface dependența numărului de unde de parametrii materialului k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }}}.
  

  .

Indicația negativă a refracției derivă matematic din tripleta vectorială E, H și k.

Pentru undele plane care se propagă în metamaterialele electromagnetice, câmpul electric, câmpul magnetic și vectorul de undă urmează o regulă de stânga, inversă comportamentului materialelor optice convenționale.

Până în prezent, numai metamaterialele prezintă un indice de refracție negativ.

Single negativeEdit

Metamaterialele single negative (SNG) au fie permitivitate relativă negativă (εr), fie permeabilitate relativă negativă (µr), dar nu ambele. Ele acționează ca metamateriale atunci când sunt combinate cu o SNG diferită, complementară, acționând împreună ca o DNG.

Mediile cu efect negativ Epsilon (ENG) prezintă o εr negativă în timp ce µr este pozitivă. Multe plasme prezintă această caracteristică. De exemplu, metalele nobile, cum ar fi aurul sau argintul, sunt ENG în spectrele infraroșu și vizibil.

Mediul Manu-negativ (MNG) prezintă un εr pozitiv și un µr negativ. Materialele giroscopice sau giromagnetice prezintă această caracteristică. Un material girotropic este un material care a fost alterat de prezența unui câmp magnetic cvasi-static, permițând un efect magneto-optic. Efectul magneto-optic este un fenomen prin care o undă electromagnetică se propagă printr-un astfel de mediu. Într-un astfel de material, polarizările eliptice cu rotație la stânga și la dreapta se pot propaga cu viteze diferite. Atunci când lumina este transmisă printr-un strat de material magneto-optic, rezultatul se numește efect Faraday: planul de polarizare poate fi rotit, formând un rotator Faraday. Rezultatele unei astfel de reflexii sunt cunoscute sub numele de efect Kerr magneto-optic (a nu se confunda cu efectul Kerr neliniar). Două materiale giroscopice cu sensuri de rotație inversate ale celor două polarizări principale se numesc izomeri optici.

Unirea unei plăci de material ENG și a unei plăci de material MNG a dus la proprietăți precum rezonanțe, tunelare anormală, transparență și reflexie zero. La fel ca și materialele cu indice negativ, SNG-urile sunt în mod înnăscut dispersive, astfel încât εr, µr și indicele de refracție n, sunt funcție de frecvență.

HyperbolicEdit

Metamaterialele hiperbolice (HMM) se comportă ca un metal pentru o anumită polarizare sau direcție de propagare a luminii și se comportă ca un dielectric pentru cealaltă datorită componentelor negative și pozitive ale tensorului de permitivitate, ceea ce conferă o anizotropie extremă. Relația de dispersie a materialului în spațiul vectorilor de undă formează un hiperboloid și, prin urmare, se numește metamaterial hiperbolic. Anizotropia extremă a HMM-urilor conduce la propagarea direcțională a luminii în interiorul și pe suprafață. HMM-urile au prezentat diverse aplicații potențiale, cum ar fi detectarea, formarea de imagini, dirijarea semnalelor optice, efecte îmbunătățite de rezonanță plasmonică.

BandgapEdit

Metamaterialele cu bandă interzisă electromagnetică (EBG sau EBM) controlează propagarea luminii. Acest lucru se realizează fie cu cristale fotonice (PC), fie cu materiale cu mâna stângă (LHM). PC-urile pot interzice complet propagarea luminii. Ambele clase pot permite propagarea luminii în direcții specifice, proiectate și ambele pot fi proiectate cu benzi interzise la frecvențele dorite. Dimensiunea perioadei EBG-urilor este o fracțiune apreciabilă a lungimii de undă, creând interferențe constructive și distructive.

PC se deosebesc de structurile sub lungimea de undă, cum ar fi metamaterialele acordabile, deoarece PC-ul își derivă proprietățile din caracteristicile benzii sale interzise. PC-urile sunt dimensionate pentru a se potrivi cu lungimea de undă a luminii, față de alte metamateriale care expun structura sub-lungimea de undă. În plus, PC-urile funcționează prin difracția luminii. În schimb, metamaterialele nu utilizează difracția.

PC-urile au incluziuni periodice care inhibă propagarea undelor datorită interferenței distructive a incluziunilor din cauza împrăștierii. Proprietatea de bandă interzisă fotonică a PC-urilor le transformă în analogul electromagnetic al cristalelor electronice semiconductoare.

EBG-urile au ca obiectiv crearea unor structuri dielectrice periodice, periodice, de înaltă calitate, cu pierderi reduse. Un EBG afectează fotonii în același mod în care materialele semiconductoare afectează electronii. PC-urile sunt materialele cu banda interzisă perfectă, deoarece nu permit propagarea luminii. Fiecare unitate a structurii periodice prescrise se comportă ca un atom, deși de dimensiuni mult mai mari.

Beg-urile sunt concepute pentru a împiedica propagarea unei lățimi de bandă alocate de frecvențe, pentru anumite unghiuri de sosire și polarizări. Au fost propuse diverse geometrii și structuri pentru a fabrica proprietățile speciale ale EBG-urilor. În practică, este imposibil să se construiască un dispozitiv EBG fără cusur.

S-au fabricat EBG-uri pentru frecvențe cuprinse între câțiva gigahertzi (GHz) și câțiva terahertzi (THz), în regiunile de frecvențe radio, microunde și infraroșu mediu. Dezvoltările aplicațiilor EBG includ o linie de transmisie, stâlpi de lemn realizați din bare dielectrice pătrate și mai multe tipuri diferite de antene cu câștig redus.

Mediul dublu pozitivEdit

Mediile dublu pozitive (DPS) există în natură, cum ar fi dielectricii naturali. Permittivitatea și permeabilitatea magnetică sunt ambele pozitive, iar propagarea undelor se face în direcția înainte. Au fost fabricate materiale artificiale care combină proprietățile DPS, ENG și MNG.

Bi-izotrope și bianisotropeEdit

Clasificarea metamaterialelor în dublu sau simplu negativ, sau dublu pozitiv, presupune în mod normal că metamaterialul are răspunsuri electrice și magnetice independente descrise de ε și µ. Cu toate acestea, în multe cazuri, câmpul electric determină polarizarea magnetică, în timp ce câmpul magnetic induce polarizarea electrică, cunoscută sub numele de cuplaj magnetoelectric. Astfel de medii sunt denumite bi-izotrope. Mediile care prezintă cuplaj magnetoelectric și care sunt anizotrope (ceea ce este cazul multor structuri metamateriale), sunt denumite bi-anizotrope.

Cei patru parametri de material sunt intrinseci cuplării magnetoelectrice a mediilor bi-izotrope. Aceștia sunt intensitățile de câmp electric (E) și magnetic (H) și densitățile de flux electric (D) și magnetic (B). Acești parametri sunt ε, µ, κ și χ sau permitivitatea, permeabilitatea, puterea de chiralitate și, respectiv, parametrul Tellegen. În acest tip de medii, parametrii materialului nu variază în funcție de modificările de-a lungul unui sistem de coordonate de măsurători rotit. În acest sens, ei sunt invarianți sau scalari.

Parametrii magnetoelectrici intrinseci, κ și χ, afectează faza undei. Efectul parametrului de chiralitate este de a diviza indicele de refracție. În mediile izotrope, acest lucru duce la propagarea undei numai dacă ε și µ au același semn. În mediile bi-izotrope, cu χ presupus a fi zero, iar κ o valoare diferită de zero, apar rezultate diferite. Se poate produce fie o undă înapoi, fie o undă înainte. Alternativ, pot apărea două unde înainte sau două unde înapoi, în funcție de intensitatea parametrului de chiralitate.

În cazul general, relațiile constitutive pentru materialele bi-anizotrope se citesc D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}

unde ϵ {\displaystyle \epsilon }

și μ {\displaystyle \mu }

sunt tensorii permisivității și, respectiv, permeabilității, în timp ce ξ {\displaystyle \xi }

și ζ {\displaystyle \zeta }

sunt cei doi tensori magneto-electrici. Dacă mediul este reciproc, permitivitatea și permeabilitatea sunt tensori simetrici, iar ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}.

, unde κ {\displaystyle \kappa }

este tensorul chiral care descrie răspunsul chiral electromagnetic și magneto-electric reciproc. Tensorul chiral poate fi exprimat ca κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}

, unde tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

este urma lui κ {\displaystyle \kappa }

, I este matricea identitate, N este un tensor simetric fără urme, iar J este un tensor antisimetric. O astfel de descompunere ne permite să clasificăm răspunsul bianisotropic reciproc și putem identifica următoarele trei clase principale: (i) mediu chiral ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}

), (ii) medii pseudochirale ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )=0,N\neq 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}

).

ChiralEdit

Mânuirea metamaterialelor este o sursă potențială de confuzie, deoarece literatura de specialitate privind metamaterialele include două utilizări contradictorii ale termenilor stângaci și dreptaci. Primul se referă la una dintre cele două unde polarizate circular care sunt modurile de propagare în mediile chirale. Al doilea se referă la tripleta de câmp electric, câmp magnetic și vector Poynting care apar în mediile cu indice de refracție negativ, care în majoritatea cazurilor nu sunt chirale.

În general, un răspuns electromagnetic chiral și/sau bianisotrop este o consecință a chiralității geometrice 3D: metamaterialele chirale 3D sunt compuse prin încorporarea structurilor 3D-chirale într-un mediu gazdă și prezintă efecte de polarizare legate de chiralitate, cum ar fi activitatea optică și dicroismul circular. Există, de asemenea, conceptul de chiralitate 2D, iar un obiect plan se spune că este chiral dacă nu poate fi suprapus peste imaginea sa în oglindă decât dacă este ridicat din plan. S-a observat că metamaterialele chirale 2D care sunt anizotrope și cu pierderi prezintă o transmisie (reflexie, absorbție) asimetrică din punct de vedere direcțional a undelor polarizate circular datorită dicroizmului de conversie circulară. Pe de altă parte, răspunsul bianisotrop poate apărea în cazul structurilor geometrice achirale care nu posedă nici chiralitate intrinsecă 2D, nici 3D. Plum și colegii săi au investigat cuplajul magneto-electric datorat chiralității extrinseci, în cazul în care dispunerea unei structuri (achirale) împreună cu vectorul undelor de radiație este diferită de imaginea sa în oglindă, și au observat o activitate optică liniară mare și reglabilă, activitate optică neliniară, activitate optică speculară și dicroism de conversie circulară. Rizza et al. au sugerat metamateriale chirale 1D în care tensorul chiral efectiv nu este dispărut dacă sistemul este geometric unidimensional chiral (imaginea în oglindă a întregii structuri nu poate fi suprapusă pe aceasta prin utilizarea translațiilor fără rotații).

Metamaterialele chirale 3D sunt construite din materiale chirale sau rezonatoare în care parametrul de chiralitate efectivă κ {\displaystyle \kappa }

este diferit de zero. Proprietățile de propagare a undelor în astfel de metamateriale chirale demonstrează că refracția negativă poate fi realizată în metamateriale cu o puternică chiralitate și ϵ r {\displaystyle \epsilon _{r}} pozitiv.

și μ r {\displaystyle \mu _{r}}

. Acest lucru se datorează faptului că indicele de refracție n {\displaystyle n}

are valori distincte pentru undele polarizate circular stânga și dreapta, date de

n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}}\pm \kappa }

Se poate observa că un indice negativ va apărea pentru o polarizare dacă κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}

. În acest caz, nu este necesar ca oricare dintre cele două ϵ r {\displaystyle \epsilon _{r}} sau ambele ϵ r {\displaystyle \epsilon _{r}}.

și μ r {\displaystyle \mu _{r}}

să fie negative pentru propagarea inversă a undelor. Un indice de refracție negativ datorat chiralității a fost observat pentru prima dată simultan și independent de Plum et al. și Zhang et al. în 2009.

FSS basedEdit

Metamaterialele bazate pe suprafețe selective în funcție de frecvență blochează semnalele într-o bandă de undă și le trec pe cele din altă bandă de undă. Ele au devenit o alternativă la metamaterialele cu frecvență fixă. Ele permit schimbări opționale de frecvențe într-un singur mediu, mai degrabă decât limitările restrictive ale unui răspuns de frecvență fixă.

.