Bună ziua, oameni buni! În acest articol, voi descrie un algoritm utilizat în procesarea limbajului natural: Latent Semantic Analysis ( LSA ).
Aplicațiile majore ale acestei metode menționate mai sus sunt foarte variate în lingvistică: Compararea documentelor în spații cu dimensiuni reduse (Document Similarity), Găsirea subiectelor recurente între documente (Topic Modeling), Găsirea relațiilor dintre termeni (Text Synoymity).

Introducere

Modelul Analizei Semantice Latente este o teorie pentru modul în care reprezentările de sens
ar putea fi învățate din întâlnirea cu eșantioane mari de limbaj fără indicații explicite cu privire la modul în care acesta este structurat.
Problema la îndemână nu este supervizată, adică nu avem etichete fixe sau categorii atribuite corpusului.

Pentru a extrage și înțelege modele din documente, LSA urmează în mod inerent anumite ipoteze:
1) Semnificația propozițiilor sau documentelor este o sumă a semnificației tuturor cuvintelor care apar în ele. În general, semnificația unui anumit cuvânt este o medie a tuturor documentelor în care apare.
2) LSA presupune că asociațiile semantice dintre cuvinte nu sunt prezente în mod explicit, ci doar latent în eșantionul mare de limbaj.

Perspectivă matematică

Latent Semantic Analysis (LSA) cuprinde anumite operații matematice pentru a obține informații despre un document. Acest algoritm stă la baza modelării tematice. Ideea de bază este de a lua o matrice din ceea ce avem – documente și termeni – și de a o descompune într-o matrice separată document-tema și o matrice subiect-termen.

Primul pas este generarea matricei noastre document-termen folosind Tf-IDF Vectorizer. Aceasta poate fi construită, de asemenea, folosind un model Bag-of-Words, dar rezultatele sunt rare și nu oferă nicio semnificație problemei.
Date m documente și n cuvinte din vocabularul nostru, putem construi o matrice
m × n A în care fiecare rând reprezintă un document și fiecare coloană reprezintă un cuvânt.

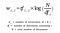
Intuitiv, un termen are o pondere mare atunci când apare frecvent în document, dar mai puțin frecvent în corpus.
Formăm o matrice document-termen, A, folosind această metodă de transformare (tf-IDF) pentru a vectoriza corpus-ul nostru. ( Într-un mod, pe care modelul nostru ulterior îl poate procesa sau evalua, deoarece deocamdată nu lucrăm cu șiruri de caractere!)
Dar există un dezavantaj subtil, nu putem deduce nimic prin observarea lui A, deoarece este o matrice zgomotoasă și rară. ( Uneori prea mare chiar și pentru a fi calculată pentru procese ulterioare).

Din moment ce Topic Modeling este în mod inerent un algoritm nesupravegheat, trebuie să specificăm subiectele latente în prealabil. Este o analogie cu K-Means Clustering astfel încât să specificăm în prealabil numărul de clustere.

În acest caz, efectuăm o aproximație Low-Rank folosind o tehnică de reducere a dimensionalității prin utilizarea unei descompuneri trunchiate a valorii singulare (SVD).
Descompunerea valorii singulare este o tehnică în algebra liniară care factorizează orice matrice M în produsul a 3 matrici separate: M=U*U*S*V, unde S este o matrice diagonală a valorilor singulare ale lui M.

SVD trunchiată reduce dimensionalitatea prin selectarea doar a celor mai mari t valori singulare și prin păstrarea doar a primelor t coloane din U și V. În acest caz, t este un hiperparametru pe care îl putem selecta și ajusta pentru a reflecta numărul de subiecte pe care dorim să le găsim.

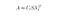
Nota: SVD trunchiat face reducerea dimensionalității și nu SVD!

Cu acești vectori de documente și vectori de termeni, putem acum aplica cu ușurință măsuri precum similaritatea cosinusului pentru a evalua:

• similitudinea diferitelor documente
• similitudinea diferitelor cuvinte
• similitudinea dintre termeni (sau „interogări”) și documente (ceea ce devine util în recuperarea informațiilor, atunci când dorim să recuperăm pasajele cele mai relevante pentru interogarea noastră de căutare).

Observații finale

Acest algoritm este utilizat în principal în diverse sarcini bazate pe NLP și reprezintă baza unor metode mai robuste, cum ar fi Probabilistic LSA și Latent Dirichlet Allocation (LDA).

Kushal Vala, Junior Data Scientist la Datametica Solutions Pvt Ltd

.