
Deși, așa cum s-a menționat în secțiunea Analiza fluxului de semnal, o anumită formă de analiză a fluxului de semnal este cel mai general mod de a trata amplificatorul cu reacție negativă, reprezentarea ca două porturi duble este abordarea cel mai des prezentată în manuale și este prezentată aici. Aceasta păstrează o partiție de circuit în două blocuri a amplificatorului, dar permite ca blocurile să fie bilaterale. Unele dezavantaje ale acestei metode sunt descrise la sfârșit.
Amplificatoarele electronice folosesc curentul sau tensiunea ca intrare și ieșire, astfel încât sunt posibile patru tipuri de amplificatoare (oricare dintre cele două intrări posibile cu oricare dintre cele două ieșiri posibile). A se vedea clasificarea amplificatoarelor. Obiectivul pentru amplificatorul cu reacție poate fi oricare dintre cele patru tipuri de amplificator și nu este neapărat de același tip cu amplificatorul în buclă deschisă, care la rândul său poate fi oricare dintre aceste tipuri. Astfel, de exemplu, un amplificator operațional (amplificator de tensiune) poate fi aranjat pentru a face în schimb un amplificator de curent.
Amplificatoarele cu reacție negativă de orice tip pot fi implementate folosind combinații de rețele cu două porturi. Există patru tipuri de rețele cu două porturi, iar tipul de amplificator dorit dictează alegerea celor două porturi și selectarea uneia dintre cele patru topologii de conectare diferite prezentate în diagramă. Aceste conexiuni sunt denumite de obicei conexiuni în serie sau în șunt (paralel). În diagramă, coloana din stânga prezintă intrările în șunt; coloana din dreapta prezintă intrările în serie. Rândul de sus prezintă ieșirile în serie; rândul de jos prezintă ieșirile în șunt. Diferitele combinații de conexiuni și de două porturi sunt enumerate în tabelul de mai jos.
| Tipul amplificatorului de reacție | Conexiune de intrare | Conexiune de ieșire | Reacțiune ideală | Două-feedback cu două porturi |
|---|---|---|---|---|
| Curent | Shunt | Serie | CCCS | g-parametru |
| Rezistență de transmisie | Shunt | Shunt | CCVS | y-…parametru |
| Transconductanță | Serie | VCCS | ||
De exemplu, pentru un amplificator cu reacție de curent, curentul de la ieșire este eșantionat pentru reacție și combinat cu curentul de la intrare. Prin urmare, retroacțiunea se realizează în mod ideal folosind o sursă de curent controlată de curent (ieșire) (CCCS), iar realizarea sa imperfectă folosind o rețea cu două porturi trebuie să încorporeze, de asemenea, o CCCS, adică alegerea adecvată pentru rețeaua de retroacțiune este o rețea cu două porturi cu parametru g. Aici este prezentată metoda cu două porturi utilizată în majoritatea manualelor, folosind circuitul tratat în articolul privind modelul de câștig asimptotic.

Figura 3 prezintă un amplificator cu doi tranzistoare cu o rezistență de reacție Rf. Scopul este de a analiza acest circuit pentru a găsi trei elemente: câștigul, impedanța de ieșire privind în amplificator dinspre sarcină și impedanța de intrare privind în amplificator dinspre sursă.
- Înlocuirea rețelei de reacție cu o rețea cu două porturiEdit
- Circuit de semnal micEdit
- Câștig în buclă deschisă încărcatEdit
- Câștig cu feedbackEdit
- Rezistențele de intrare și de ieșireEdit
- Context privind determinarea rezistențeiEdit
- Aplicarea la amplificatorul de exempluEdit
- Tensiunea de sarcină și curentul de sarcinăEdit
- Blocul amplificatorului principal este unul cu două porturi?Edit
Înlocuirea rețelei de reacție cu o rețea cu două porturiEdit
Primul pas este înlocuirea rețelei de reacție cu o rețea cu două porturi. Ce componente intră în cele două porturi?
Pe partea de intrare a celor două porturi avem Rf. Dacă tensiunea de pe partea dreaptă a lui Rf se modifică, se modifică curentul din Rf care este sustras din curentul care intră în baza tranzistorului de intrare. Adică, partea de intrare a celor două porturi este o sursă de curent dependentă, controlată de tensiunea din partea de sus a rezistorului R2.
Se poate spune că cel de-al doilea etaj al amplificatorului este doar un urmăritor de tensiune, care transmite tensiunea de la colectorul tranzistorului de intrare la partea de sus a lui R2. Altfel spus, semnalul de ieșire monitorizat este de fapt tensiunea de la colectorul tranzistorului de intrare. Acest punct de vedere este legitim, dar atunci etajul urmăritor de tensiune devine parte a rețelei de reacție. Acest lucru face ca analiza reacției de reacție să fie mai complicată.
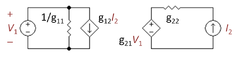
O viziune alternativă este aceea că tensiunea la vârful lui R2 este stabilită de curentul de emitor al tranzistorului de ieșire. Acest punct de vedere conduce la o rețea de reacție complet pasivă formată din R2 și Rf. Variabila care controlează retroacțiunea este curentul emițătorului, deci retroacțiunea este o sursă de curent controlată de curent (CCCS). Căutăm prin cele patru rețele cu două porturi disponibile și descoperim că singura care are o CCCS este cea cu două porturi cu parametru g, prezentată în figura 4. Următoarea sarcină este de a selecta parametrii g astfel încât rețeaua cu două porturi din figura 4 să fie echivalentă din punct de vedere electric cu secțiunea L formată din R2 și Rf. Această selecție este o procedură algebrică realizată cel mai simplu prin examinarea a două cazuri individuale: cazul cu V1 = 0, care face ca VCVS din partea dreaptă a celor două porturi să fie un scurtcircuit; și cazul cu I2 = 0, care face ca CCCS din partea stângă să fie un circuit deschis. Algebra în aceste două cazuri este simplă, mult mai ușoară decât rezolvarea pentru toate variabilele deodată. Alegerea parametrilor g care fac ca cele două porturi și secțiunea L să se comporte în același mod sunt prezentate în tabelul de mai jos.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{\mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 R 2 + R f {\displaystyle -{\frac {R_{2}}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 R 2 R 2 + R f {\displaystyle {\frac {R_{2}}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
 |
Circuit de semnal micEdit
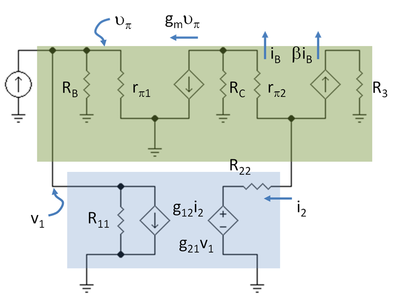
Postul următor este de a desena schema de semnal mic pentru amplificatorul cu două porturi în loc, folosind modelul hibrid-pi pentru tranzistori. Figura 5 prezintă schema cu notația R3 = RC2 // RL și R11 = 1 / g11, R22 = g22.
Câștig în buclă deschisă încărcatEdit
Figura 3 indică nodul de ieșire, dar nu și alegerea variabilei de ieșire. O alegere utilă este ieșirea de curent de scurtcircuit a amplificatorului (ceea ce conduce la câștigul de curent de scurtcircuit). Deoarece această variabilă conduce simplu la oricare dintre celelalte alegeri (de exemplu, tensiunea de sarcină sau curentul de sarcină), câștigul curentului de scurtcircuit se găsește mai jos.
Prima dată se găsește câștigul în buclă deschisă încărcat. Reacția este dezactivată prin setarea g12 = g21 = 0. Ideea este de a afla cât de mult se modifică câștigul amplificatorului din cauza rezistențelor din rețeaua de reacție prin ele însele, cu reacția dezactivată. Acest calcul este destul de ușor, deoarece R11, RB și rπ1 sunt toate în paralel și v1 = vπ. Fie R1 = R11 // RB // rπ1. În plus, i2 = -(β+1) iB. Rezultatul pentru câștigul de curent în buclă deschisă AOL este:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\displaystyle A_{\mathrm {OL} }={\frac {\beta i_{\mathrm {B} }}}}{i_{\mathrm {S} }}}=g_{{m}R_{\mathrm {C} }\left({\frac {\beta }{\beta +1}}\right)\left({\frac {R_{1}}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C} }}}{\beta +1}}}}\right)\}.

Câștig cu feedbackEdit
În abordarea clasică a feedback-ului, feedforward-ul reprezentat de VCVS (adică g21 v1) este neglijat. Acest lucru face ca circuitul din figura 5 să semene cu schema bloc din figura 1, iar câștigul cu reacție este atunci:
A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}}{1+{{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}}}{1+{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}A_{{\mathrm {OL} }}}}\ ,}

unde factorul de reacție βFB = -g12. Se introduce notația βFB pentru factorul de reacție pentru a-l distinge de tranzistorul β.
Rezistențele de intrare și de ieșireEdit

Rezistența de reacție este utilizată pentru a adapta mai bine sursele de semnal la sarcinile acestora. De exemplu, o conexiune directă a unei surse de tensiune la o sarcină rezistivă poate duce la pierderea semnalului din cauza diviziunii tensiunii, dar intercalarea unui amplificator cu reacție negativă poate crește sarcina aparentă văzută de sursă și poate reduce impedanța aparentă a driverului văzută de sarcină, evitând atenuarea semnalului prin diviziunea tensiunii. Acest avantaj nu se limitează la amplificatoarele de tensiune, ci se pot aranja îmbunătățiri analoage în ceea ce privește adaptarea pentru amplificatoare de curent, amplificatoare de transconductanță și amplificatoare de rezistență.
Pentru a explica aceste efecte ale retroacțiunii asupra impedanțelor, mai întâi o digresiune asupra modului în care teoria celor două porturi abordează determinarea rezistenței, și apoi aplicarea ei la amplificatorul de față.
Context privind determinarea rezistențeiEdit
Figura 6 prezintă un circuit echivalent pentru aflarea rezistenței de intrare a unui amplificator de tensiune cu reacție (stânga) și pentru un amplificator de curent cu reacție (dreapta). Aceste aranjamente sunt aplicații tipice ale teoremei lui Miller.
În cazul amplificatorului de tensiune, tensiunea de ieșire βVout a rețelei de reacție este aplicată în serie și cu o polaritate opusă tensiunii de intrare Vx care parcurge bucla (dar în raport cu masa, polaritățile sunt aceleași). Ca urmare, tensiunea efectivă la bornele și curentul prin rezistența de intrare Rin a amplificatorului scad, astfel încât rezistența de intrare a circuitului crește (se poate spune că Rin aparent crește). Noua sa valoare poate fi calculată prin aplicarea teoremei Miller (pentru tensiuni) sau a legilor circuitului de bază. Astfel, legea tensiunii lui Kirchhoff prevede:
V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} }+\beta v_{\mathrm {out} } ,}

unde vout = Av vin = Av Ix Rin. Înlocuind acest rezultat în ecuația de mai sus și rezolvând pentru rezistența de intrare a amplificatorului cu reacție, rezultatul este:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}=\left(1+\beta A_{v}\right)R_{\mathrm {in} }\ .}

Concluzia generală din acest exemplu și dintr-un exemplu similar pentru cazul rezistenței de ieșire este: O conexiune de reacție în serie la intrare (ieșire) mărește rezistența de intrare (ieșire) cu un factor ( 1 + β AOL ), unde AOL = câștigul în buclă deschisă.
Pe de altă parte, pentru amplificatorul de curent, curentul de ieșire βIout al rețelei de reacție este aplicat în paralel și cu sens opus curentului de intrare Ix. Ca urmare, curentul total care circulă prin circuitul de intrare (nu numai prin rezistența de intrare Rin) crește, iar tensiunea la bornele acestuia scade, astfel încât rezistența de intrare a circuitului scade (aparent Rin scade). Noua sa valoare poate fi calculată prin aplicarea teoremei duale a lui Miller (pentru curenți) sau a legilor de bază ale lui Kirchhoff:
I x = V i n R i n + β i o u t . {\displaystyle I_{x}={\frac {V_{\mathrm {in} }}}}{R_{\mathrm {in} }}}+\beta i_{\mathrm {out} }\ .}

unde iout = Ai iin = Ai Vx / Rin. Înlocuind acest rezultat în ecuația de mai sus și rezolvând pentru rezistența de intrare a amplificatorului de reacție, rezultatul este:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}}={\frac {R_{\mathrm {in} }}}{\left(1+\beta A_{i}\right)}}}}\ .}

Concluzia generală din acest exemplu și dintr-un exemplu similar pentru cazul rezistenței de ieșire este: O conexiune de reacție paralelă la intrare (ieșire) scade rezistența de intrare (ieșire) cu un factor ( 1 + β AOL ), unde AOL = câștigul buclei deschise.
Aceste concluzii pot fi generalizate pentru a trata cazuri cu acționări Norton sau Thévenin arbitrare, sarcini arbitrare și rețele generale de reacție cu două porturi. Cu toate acestea, rezultatele depind de faptul că amplificatorul principal are o reprezentare ca o rețea cu două porturi – adică rezultatele depind de același curent care intră și iese de la bornele de intrare și, de asemenea, același curent care iese de la o bornă de ieșire trebuie să intre la cealaltă bornă de ieșire.
O concluzie mai amplă, independentă de detaliile cantitative, este că retroacțiunea poate fi folosită pentru a mări sau a micșora impedanța de intrare și de ieșire.
Aplicarea la amplificatorul de exempluEdit
Aceste rezultate privind rezistența se aplică acum la amplificatorul din figura 3 și figura 5. Factorul de îmbunătățire care reduce câștigul, și anume ( 1 + βFB AOL), decide în mod direct efectul retroacțiunii asupra rezistențelor de intrare și de ieșire ale amplificatorului. În cazul unei conexiuni în derivație, impedanța de intrare se reduce cu acest factor; iar în cazul unei conexiuni în serie, impedanța se înmulțește cu acest factor. Cu toate acestea, impedanța care este modificată de reacție este impedanța amplificatorului din figura 5 cu reacție dezactivată și include modificările de impedanță cauzate de rezistențele din rețeaua de reacție.
În consecință, impedanța de intrare văzută de sursă cu retroacțiunea dezactivată este Rin = R1 = R11 // RB // rπ1, iar cu retroacțiunea activată (dar fără feedforward)
R i n = R 1 1 + β F B A O L , {\displaystyle R_{\mathrm {in} }={\frac {R_{1}}{1+{\beta }_{\mathrm {FB} }A_{\mathrmathrm {OL} }}}}} ,}

unde se folosește diviziunea deoarece conexiunea de intrare este în derivație: conexiunea de reacție cu două porturi este în paralel cu sursa de semnal de la intrarea amplificatorului. O reamintire: AOL este câștigul în buclă deschisă cu sarcină găsit mai sus, modificat de rezistențele rețelei de reacție.
Impedanța văzută de sarcină necesită o discuție suplimentară. Sarcina din figura 5 este conectată la colectorul tranzistorului de ieșire și, prin urmare, este separată de corpul amplificatorului de impedanța infinită a sursei de curent de ieșire. Prin urmare, retroacțiunea nu are nici un efect asupra impedanței de ieșire, care rămâne pur și simplu RC2, așa cum este văzută de rezistența de sarcină RL din figura 3.
Dacă în schimb am dori să găsim impedanța prezentată la emitorul tranzistorului de ieșire (în loc de colectorul acestuia), care este conectat în serie la rețeaua de reacție, retroacțiunea ar crește această rezistență cu factorul de îmbunătățire ( 1 + βFB AOL).
Tensiunea de sarcină și curentul de sarcinăEdit
Câștigul derivat mai sus este câștigul de curent la colectorul tranzistorului de ieșire. Pentru a relaționa acest câștig cu câștigul atunci când tensiunea este la ieșirea amplificatorului, observați că tensiunea de ieșire la sarcina RL este legată de curentul de colector prin legea lui Ohm ca vL = iC (RC2 || RL). În consecință, câștigul de tranzistanță vL / iS se găsește prin înmulțirea câștigului de curent cu RC2 || RL:
v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{\mathrm {L} }}}}}}{i_{\mathrm {S} }}}=A_{{\mathrm {FB} }(R_{{\mathrm {C2} }\paralelă R_{\mathrm {L} })\ .}

În mod similar, dacă ieșirea amplificatorului este considerată a fi curentul din rezistența de sarcină RL, diviziunea curentului determină curentul de sarcină, iar câștigul este atunci:
i L i S = A F B R C 2 R C 2 + R L . {\displaystyle {\frac {i_{\mathrm {L} }}{i_{\mathrm {S} }}}=A_{{\mathrm {FB} }{\frac {R_{\mathrmathrm {C2} }}}}{R_{\mathrm {C2} }+R_{{\mathrm {L} }}}\ .}

Blocul amplificatorului principal este unul cu două porturi?Edit

În cele ce urmează sunt prezentate câteva dezavantaje ale abordării cu două porturi, destinate cititorului atent.
Figura 7 prezintă schema de semnal mic cu amplificatorul principal și portul dublu de reacție în casete umbrite. Reacția cu două porturi de reacție satisface condițiile de port: la portul de intrare, Iin intră și iese din port și, la fel, la ieșire, Iout intră și iese.
Blocul amplificatorului principal este, de asemenea, un bloc cu două porturi? Amplificatorul principal este prezentat în caseta umbrită de sus. Conexiunile de masă sunt etichetate. Figura 7 arată faptul interesant că amplificatorul principal nu satisface condițiile de port la intrarea și la ieșirea sa decât dacă conexiunile de masă sunt alese astfel încât să se întâmple acest lucru. De exemplu, pe partea de intrare, curentul care intră în amplificatorul principal este IS. Acest curent este împărțit în trei moduri: către rețeaua de reacție, către rezistența de polarizare RB și către rezistența de bază a tranzistorului de intrare rπ. Pentru a satisface condiția de port pentru amplificatorul principal, toate cele trei componente trebuie să se întoarcă pe partea de intrare a amplificatorului principal, ceea ce înseamnă că toate cablurile de masă etichetate G1 trebuie să fie conectate, precum și cablul emițătorului GE1. În mod similar, pe partea de ieșire, toate conexiunile de masă G2 trebuie să fie conectate, precum și conexiunea de masă GE2. Apoi, în partea de jos a schemei, sub portul dublu de reacție și în afara blocurilor amplificatorului, G1 este conectat la G2. Acest lucru forțează curenții de masă să se împartă între partea de intrare și cea de ieșire, așa cum a fost planificat. Observați că acest aranjament de conectare împarte emițătorul tranzistorului de intrare într-o latură de bază și una de colector – un lucru imposibil de făcut din punct de vedere fizic, dar din punct de vedere electric circuitul vede toate conexiunile de masă ca pe un singur nod, așa că această ficțiune este permisă.
Desigur, modul în care sunt conectați conductorii de masă nu face nici o diferență pentru amplificator (toți sunt un singur nod), dar face o diferență în ceea ce privește condițiile de port. Această artificialitate este o slăbiciune a acestei abordări: condițiile de port sunt necesare pentru a justifica metoda, dar circuitul nu este cu adevărat afectat de modul în care se face schimbul de curenți între conexiunile de masă.
Cu toate acestea, dacă niciun aranjament posibil al condițiilor de masă nu conduce la condițiile de port, circuitul ar putea să nu se comporte în același mod. Factorii de îmbunătățire (1 + βFB AOL) pentru determinarea impedanței de intrare și de ieșire ar putea să nu funcționeze. Această situație este incomodă, deoarece eșecul de a realiza un circuit cu două porturi poate reflecta o problemă reală (pur și simplu nu este posibil), sau poate reflecta o lipsă de imaginație (de exemplu, pur și simplu nu s-a gândit să împartă nodul emițător în două). În consecință, atunci când condițiile de port sunt îndoielnice, sunt posibile cel puțin două abordări pentru a stabili dacă factorii de îmbunătățire sunt exacți: fie se simulează un exemplu folosind Spice și se compară rezultatele cu utilizarea unui factor de îmbunătățire, fie se calculează impedanța folosind o sursă de testare și se compară rezultatele.
O alegere mai practică este de a renunța complet la abordarea cu două porturi și de a folosi diverse alternative bazate pe teoria grafurilor de flux de semnal, inclusiv metoda Rosenstark, metoda Choma și utilizarea teoremei lui Blackman. Această alegere poate fi recomandabilă în cazul în care modelele dispozitivelor de semnal mic sunt complexe sau nu sunt disponibile (de exemplu, dispozitivele sunt cunoscute doar numeric, poate din măsurători sau din simulări SPICE).
.