#InsideRL

Într-o problemă tipică de învățare prin întărire (RL), există un învățător și un factor de decizie numit agent, iar mediul înconjurător cu care acesta interacționează se numește mediu. Mediul, în schimb, oferă recompense și o nouă stare în funcție de acțiunile agentului. Așadar, în învățarea prin întărire, nu învățăm un agent cum ar trebui să facă ceva, ci îi oferim recompense, pozitive sau negative, în funcție de acțiunile sale. Așadar, întrebarea de bază pentru acest blog este cum formulăm matematic orice problemă în RL. Aici intervine procesul de decizie Markov (MDP).

Înainte de a răspunde la întrebarea noastră de bază, și anume Cum formulăm matematic problemele de RL (folosind MDP), trebuie să ne dezvoltăm intuiția despre :

• Relația agent-mediu
• Proprietatea Markov
• Procesul Markov și lanțurile Markov
• Procesul de recompensă Markov (MRP)
• Ecuația Bellman
• Procesul de recompensă Markov

Căutați-vă cafeaua și nu vă opriți până când nu sunteți mândri!🧐

Relația agent-mediu

În primul rând să analizăm câteva definiții formale :

Agent : Programe software care iau decizii inteligente și care sunt cursanții în RL. Acești agenți interacționează cu mediul prin acțiuni și primesc recompense în funcție de acțiunile lor.

Mediu :Este demonstrația problemei de rezolvat.Acum, putem avea un mediu din lumea reală sau un mediu simulat cu care agentul nostru va interacționa.

Stare : Aceasta este poziția agenților la un anumit pas de timp în mediul înconjurător. astfel, ori de câte ori un agent efectuează o acțiune, mediul îi oferă agentului o recompensă și o nouă stare în care agentul a ajuns prin efectuarea acțiunii.

Se consideră că tot ceea ce agentul nu poate schimba în mod arbitrar face parte din mediu. În termeni simpli, acțiunile pot fi orice decizie pe care dorim ca agentul să o învețe, iar starea poate fi orice lucru care poate fi util în alegerea acțiunilor. Nu presupunem că tot ceea ce există în mediul înconjurător este necunoscut agentului, de exemplu, calculul recompensei este considerat ca făcând parte din mediul înconjurător, chiar dacă agentul știe câte ceva despre modul în care este calculată recompensa sa în funcție de acțiunile sale și de stările în care acestea sunt întreprinse. Acest lucru se datorează faptului că recompensele nu pot fi modificate în mod arbitrar de către agent. Uneori, agentul poate fi pe deplin conștient de mediul în care se află, dar, cu toate acestea, întâmpină dificultăți în maximizarea recompensei, la fel ca atunci când știm cum să jucăm cubul Rubik, dar nu reușim să-l rezolvăm. Așadar, putem spune cu certitudine că relația agent-mediu reprezintă limita controlului agentului și nu cunoașterea acestuia.

Proprietatea Markov

Tranziție: Trecerea de la o stare la alta se numește tranziție.

Probabilitatea tranziției: Probabilitatea ca agentul să treacă de la o stare la alta se numește probabilitate de tranziție.

Proprietatea Markov afirmă că :

„Viitorul este independent de trecut având în vedere prezentul”

Matematic putem exprima această afirmație sub forma :

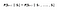
S denotă starea actuală a agentului și s denotă starea următoare. Ceea ce înseamnă această ecuație este că tranziția de la starea S la S este complet independentă de trecut. Așadar, RHS a ecuației are aceeași semnificație ca și LHS dacă sistemul are o proprietate Markov. În mod intuitiv înseamnă că starea noastră curentă captează deja informațiile din stările trecute.

Probabilitatea de tranziție a stării :

Cum știm acum despre probabilitatea de tranziție, putem defini probabilitatea de tranziție a stării după cum urmează :

Pentru starea Markov de la S la S, adică orice altă stare succesoare , probabilitatea de tranziție a stării este dată de

Potem formula probabilitatea de tranziție a stării într-o matrice de probabilitate de tranziție a stării prin :

Care rând din matrice reprezintă probabilitatea de a trece de la starea noastră inițială sau de pornire la orice stare succesoare.Suma fiecărui rând este egală cu 1.

Procesul Markov sau lanțurile Markov

Procesul Markov este un proces aleatoriu fără memorie, adică o secvență de stări aleatoare S,S,….S cu o proprietate Markov.Deci, este practic o secvență de stări cu proprietatea Markov.Poate fi definit folosind un set de stări (S) și o matrice de probabilitate de tranziție (P).Dinamica mediului poate fi complet definită folosind un set de stări(S) și matricea de probabilitate de tranziție(P).

Dar ce înseamnă proces aleator ?

Pentru a răspunde la această întrebare să ne uităm la un exemplu:

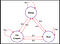
Arginile arborelui denotă probabilitatea de tranziție. Din acest lanț să luăm un eșantion. Acum, să presupunem că dormeam și că, conform distribuției de probabilitate, există 0,6 șanse să alergăm și 0,2 șanse să dormim mai mult și din nou 0,2 șanse să mâncăm înghețată. În mod similar, ne putem gândi la alte secvențe pe care le putem eșantiona din acest lanț.

Câteva eșantioane din lanț :

• Sleep – Run – Ice-cream – Sleep
• Sleep – Ice-cream – Ice-cream – Run

În cele două secvențe de mai sus, ceea ce vedem este că obținem un set aleatoriu de stări (S) (adică Sleep, Ice-cream, Sleep ) de fiecare dată când rulăm lanțul.Sper că acum este clar de ce procesul Markov se numește set aleatoriu de secvențe.

Înainte de a trece la procesul Markov Reward, să analizăm câteva concepte importante care ne vor ajuta să înțelegem MRP.

Recompense și returnări

Recompensele sunt valorile numerice pe care le primește agentul la efectuarea unei anumite acțiuni în anumite stări din mediu. Valoarea numerică poate fi pozitivă sau negativă în funcție de acțiunile agentului.

În învățarea prin întărire, ne interesează maximizarea recompensei cumulative (toate recompensele pe care le primește agentul din mediul înconjurător) în loc de, recompensa pe care o primește agentul din starea curentă (numită și recompensă imediată). Această sumă totală a recompenselor pe care agentul le primește de la mediu se numește randament.

Potem defini returnările ca fiind :

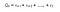
r este recompensa primită de agent la pasul de timp t în timp ce efectuează o acțiune(a) pentru a trece dintr-o stare în alta. În mod similar, r este recompensa primită de agent la pasul de timp t prin efectuarea unei acțiuni pentru a se deplasa într-o altă stare. Și, r este recompensa primită de agent la pasul de timp final prin efectuarea unei acțiuni pentru a se deplasa într-o altă stare.

Sarcini episodice și continue

Sarcini episodice: Acestea sunt sarcinile care au o stare terminală (stare finală). putem spune că au stări finite. De exemplu, în jocurile de curse, începem jocul (începem cursa) și îl jucăm până când jocul se termină (cursa se termină!). Acest lucru se numește episod. Odată ce repornim jocul, acesta va porni de la o stare inițială și, prin urmare, fiecare episod este independent.

Sarcini continue : Acestea sunt sarcinile care nu au sfârșit, adică nu au o stare terminală.Aceste tipuri de sarcini nu se vor termina niciodată.De exemplu, să înveți cum să codezi!

Acum, este ușor de calculat randamentul sarcinilor episodice, deoarece acestea se vor termina în cele din urmă, dar cum rămâne cu sarcinile continue, deoarece vor continua la nesfârșit. Randamentele de la se adună până la infinit! Deci, cum definim randamentele pentru sarcinile continue?

Aici avem nevoie de Factorul de actualizare (ɤ).

Factorul de actualizare (ɤ): Acesta determină câtă importanță trebuie acordată recompensei imediate și recompenselor viitoare. Acesta ne ajută practic să evităm infinitul ca recompensă în sarcinile continue. Are o valoare între 0 și 1. O valoare de 0 înseamnă că se acordă mai multă importanță recompensei imediate, iar o valoare de 1 înseamnă că se acordă mai multă importanță recompenselor viitoare. În practică, un factor de actualizare de 0 nu va învăța niciodată, deoarece ia în considerare doar recompensa imediată, iar un factor de actualizare de 1 va continua pentru recompensele viitoare, ceea ce poate duce la infinit. Prin urmare, valoarea optimă pentru factorul de actualizare se situează între 0,2 și 0,8.

Atunci, putem defini randamentele folosind factorul de actualizare după cum urmează :(Să spunem că aceasta este ecuația 1, deoarece vom folosi această ecuație mai târziu pentru derivarea ecuației Bellman)

Să o înțelegem cu un exemplu,să presupunem că locuiți într-un loc în care vă confruntați cu o penurie de apă, deci dacă cineva vine la dumneavoastră și vă spune că vă va da 100 de litri de apă!(presupuneți vă rog!) pentru următoarele 15 ore în funcție de un anumit parametru (ɤ).Să analizăm două posibilități : (Să spunem că aceasta este ecuația 1 ,deoarece vom folosi această ecuație mai târziu pentru derivarea ecuației Bellman)

Una cu factorul de actualizare (ɤ) 0.8 :

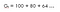
Aceasta înseamnă că ar trebui să așteptăm până în a 15-a oră, deoarece scăderea nu este foarte semnificativă , așa că merită să mergem până la sfârșit. înseamnă că suntem interesați și de recompensele viitoare.Deci, dacă factorul de actualizare este aproape de 1, atunci vom face un efort să mergem până la sfârșit, deoarece recompensa are o importanță semnificativă.

Secunde, cu factorul de actualizare (ɤ) 0,2 :

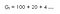
Aceasta înseamnă că suntem mai interesați de recompensele timpurii, deoarece recompensele devin semnificativ mai mici la o oră.Deci, s-ar putea să nu vrem să așteptăm până la sfârșit (până la a 15-a oră), deoarece vor fi lipsite de valoare.Deci, dacă factorul de actualizare este aproape de zero, atunci recompensele imediate sunt mai importante decât cele viitoare.

Atunci ce valoare a factorului de actualizare să folosim?

Depinde de sarcina pentru care dorim să antrenăm un agent. Să presupunem că, într-un joc de șah, scopul este de a învinge regele adversarului. Dacă acordăm importanță recompenselor imediate, cum ar fi o recompensă la înfrângerea pionului oricărui jucător advers, atunci agentul va învăța să îndeplinească aceste sub-obiective, indiferent dacă și jucătorii săi sunt învinși. Așadar, în această sarcină, recompensele viitoare sunt mai importante. În unele cazuri, am putea prefera să folosim recompense imediate, cum ar fi exemplul cu apa pe care l-am văzut mai devreme.

Procesul de recompensă Markov

Până acum am văzut cum lanțul Markov a definit dinamica unui mediu folosind un set de stări (S) și o matrice de probabilitate de tranziție (P).Dar, știm că învățarea prin întărire are ca obiectiv maximizarea recompensei.Deci, să adăugăm recompensa la lanțul nostru Markov.Acest lucru ne oferă procesul de recompensă Markov.

Procesul de recompensă Markov: După cum sugerează și numele, MDP-urile sunt lanțuri Markov cu judecata valorilor.Practic, obținem o valoare din fiecare stare în care se află agentul nostru.

Matematic, definim procesul de recompensă Markov ca fiind :

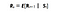
Ce înseamnă această ecuație este câtă recompensă (Rs) obținem dintr-o anumită stare S. Aceasta ne spune recompensa imediată din acea anumită stare în care se află agentul nostru. După cum vom vedea în povestea următoare, cum maximizăm aceste recompense din fiecare stare în care se află agentul nostru. În termeni simpli, maximizăm recompensa cumulativă pe care o obținem din fiecare stare.

Definim MRP ca fiind (S,P,R,ɤ) ,unde :

• S este un set de stări,
• P este matricea probabilităților de tranziție,
• R este funcția de recompensă , pe care am văzut-o mai devreme,
• ɤ este factorul de actualizare

Procesul decizional Markov

Acum, să dezvoltăm intuiția noastră pentru ecuația Bellman și procesul decizional Markov.

Funcția de politică și funcția de valoare

Funcția de valoare determină cât de bine este pentru agent să se afle într-o anumită stare. Desigur, pentru a determina cât de bine va fi să se afle într-o anumită stare trebuie să depindă de anumite acțiuni pe care le va întreprinde. Aici intervine politica. O politică definește ce acțiuni să efectueze într-o anumită stare s.

O politică este o funcție simplă, care definește o distribuție de probabilitate asupra acțiunilor (a∈ A) pentru fiecare stare (s ∈ S). Dacă un agent la momentul t urmează o politică π, atunci π(a|s) este probabilitatea ca agentul cu să ia o acțiune (a ) la un anumit pas de timp (t). în învățarea prin întărire, experiența agentului determină schimbarea politicii. Din punct de vedere matematic, o politică este definită după cum urmează :

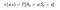
Acum, cum găsim o valoare a unei stări.Valoarea stării s, atunci când agentul urmează o politică π care este notată cu vπ(s) este randamentul așteptat pornind de la s și urmând o politică π pentru următoarele stări,până când ajungem la starea terminală.O putem formula astfel :(Această funcție se mai numește și Funcția valoare de stare)

Această ecuație ne oferă randamentele așteptate pornind de la starea(s) și mergând la stările succesoare ulterioare, cu politica π. Un lucru care trebuie remarcat este că randamentele pe care le obținem sunt stocastice, în timp ce valoarea unei stări nu este stocastică. Aceasta este așteptarea randamentelor din starea inițială s și, ulterior, din orice altă stare. De asemenea, rețineți că valoarea stării terminale (dacă există) este zero. Să vedem un exemplu :

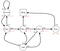
Să presupunem că starea noastră de pornire este clasa 2, și trecem la clasa 3, apoi la Pass și apoi la Sleep.Pe scurt, clasa 2 > clasa 3 > Pass > Sleep.

Rentabilitatea noastră așteptată este cu factorul de actualizare 0,5:

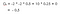
Nota:Este -2 + (-2 * 0.5) + 10 * 0,25 + 0 în loc de -2 * -2 * 0,5 + 10 * 0,25 + 0.Atunci valoarea clasei 2 este -0,5 .

Ecuația Bellman pentru funcția de valoare

Ecuația Bellman ne ajută să găsim politicile optime și funcția de valoare.Știm că politica noastră se schimbă odată cu experiența, astfel încât vom avea o funcție de valoare diferită în funcție de diferite politici.Funcția de valoare optimă este cea care oferă valoarea maximă în comparație cu toate celelalte funcții de valoare.

Ecuația Bellman afirmă că funcția de valoare poate fi descompusă în două părți:

• Recompensă imediată, R
• Valoare actualizată a stărilor succesoare,

Matematic, putem defini ecuația Bellman ca fiind :

Să înțelegem ce spune această ecuație cu ajutorul unui exemplu :

Să presupunem că există un robot într-o anumită stare (s) și apoi el se deplasează din această stare într-o altă stare (s’). Acum, întrebarea este cât de bine a fost pentru robot să se afle în acea stare (s). Utilizând ecuația Bellman, putem spune că este vorba de așteptarea recompensei pe care a primit-o la părăsirea stării (s) plus valoarea stării (s’) în care s-a mutat.

Să ne uităm la un alt exemplu :

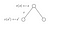
Vrem să cunoaștem valoarea stării s.Valoarea stării (s) este recompensa pe care am obținut-o la părăsirea acelei stări, plus valoarea actualizată a stării în care am aterizat înmulțită cu probabilitatea de tranziție în care ne vom muta în ea.

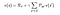
Ecuația de mai sus poate fi exprimată sub formă de matrice după cum urmează :

Unde v este valoarea stării în care ne aflam, care este egală cu recompensa imediată plus valoarea actualizată a următoarei stări înmulțită cu probabilitatea de a trece în acea stare.

Complexitatea timpului de execuție pentru acest calcul este O(n³). Prin urmare, este clar că aceasta nu este o soluție practică pentru rezolvarea MRP-urilor mari (la fel și pentru MDP-uri). în blogurile ulterioare, vom examina metode mai eficiente, cum ar fi Programarea dinamică (iterația valorii și iterația politicii), metodele Monte-Claro și TD-Learning.

Vom vorbi despre Ecuația Bellman în mult mai multe detalii în următoarea povestire.

Ce este Procesul de Decizie Markov?

Procesul de Decizie Markov : Este Procesul de Recompensă Markov cu o decizie.Totul este la fel ca MRP, dar acum avem o agenție reală care ia decizii sau întreprinde acțiuni.

Este un tuplu de (S, A, P, R, 𝛾) unde:

• S este un set de stări,
• A este setul de acțiuni pe care agentul poate alege să le întreprindă,
• P este matricea probabilităților de tranziție,
• R este recompensa acumulată prin acțiunile agentului,
• 𝛾 este factorul de actualizare.

P și R vor avea ușoare modificări în funcție de acțiuni, după cum urmează :

Matrice de probabilitate de tranziție

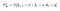
Funcția de recompensă

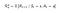
Acum, funcția noastră de recompensă este dependentă de acțiune.

Până acum am vorbit despre obținerea unei recompense (r) atunci când agentul nostru trece printr-un set de stări (s) urmând o politică π.De fapt, în procesul decizional Markov (MDP), politica este mecanismul de luare a deciziilor.Așadar, acum avem un mecanism care va alege să întreprindă o acțiune.

Politica într-un MDP depinde de starea curentă.Ea nu depinde de istoric.Aceasta este proprietatea Markov.Deci, starea curentă în care ne aflăm caracterizează istoricul.

Am văzut deja cât de bine este pentru agent să se afle într-o anumită stare (Funcția stare-valoare).Acum, să vedem cât de bine este să întreprindă o anumită acțiune urmând o politică π din starea s (Funcția acțiune-valoare).

Funcția stare-valoare-acțiune sau Funcția Q

Această funcție specifică cât de bine este pentru agent să întreprindă o acțiune (a) într-o stare (s) cu o politică π.

Matematic, putem defini funcția de valoare a acțiunii de stat ca fiind :

În principiu, aceasta ne spune valoarea efectuării unei anumite acțiuni (a) într-o stare (s) cu o politică π.

Să ne uităm la un exemplu de proces de decizie Markov :

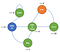
Acum, putem vedea că nu mai există probabilități.De fapt, acum agentul nostru are de făcut alegeri, cum ar fi după ce se trezește ,putem alege să ne uităm la netflix sau să codăm și să depanăm.Desigur, acțiunile agentului sunt definite în raport cu o anumită politică π și va primi recompensa în consecință.

.