
Ale, jak wspomniano w rozdziale Analiza przepływów sygnałów, jakaś forma analizy przepływów sygnałów jest najbardziej ogólnym sposobem traktowania wzmacniacza o ujemnym sprzężeniu zwrotnym, reprezentacja jako dwa dwuporty jest podejściem najczęściej prezentowanym w podręcznikach i jest przedstawiona tutaj. Zachowuje ono dwublokowy podział obwodu wzmacniacza, ale pozwala na to, aby bloki były dwustronne. Niektóre wady tej metody są opisane na końcu.
Wzmacniacze elektroniczne używają prądu lub napięcia jako wejścia i wyjścia, więc cztery typy wzmacniaczy są możliwe (dowolne z dwóch możliwych wejść z dowolnymi z dwóch możliwych wyjść). Zobacz klasyfikację wzmacniaczy. Celem wzmacniacza ze sprzężeniem zwrotnym może być dowolny z czterech typów wzmacniaczy i niekoniecznie jest to ten sam typ co wzmacniacz w otwartej pętli, który sam może być dowolnym z tych typów. Tak więc, na przykład, wzmacniacz op amp (wzmacniacz napięcia) może być ułożony tak, aby zamiast niego powstał wzmacniacz prądu.
Wzmacniacze z ujemnym sprzężeniem zwrotnym dowolnego typu mogą być realizowane przy użyciu kombinacji sieci dwuportowych. Istnieją cztery typy sieci dwuportowych, a typ pożądanego wzmacniacza dyktuje wybór dwóch portów i wybór jednej z czterech różnych topologii połączeń pokazanych na rysunku. Połączenia te są zwykle określane jako połączenia szeregowe lub bocznikujące (równoległe). Na diagramie, lewa kolumna pokazuje wejścia bocznikowe; prawa kolumna pokazuje wejścia szeregowe. Górny rząd pokazuje wyjścia szeregowe; dolny rząd pokazuje wyjścia bocznikowe. Różne kombinacje połączeń i dwuportów są wymienione w poniższej tabeli.
| Typ wzmacniacza ze sprzężeniem zwrotnym | Połączenie wejściowe | Połączenie wyjściowe | Idealne sprzężenie zwrotne | Dwa-portowe sprzężenie zwrotne |
|---|---|---|---|---|
| Prąd | Shunt | Seria | CCCS | g-parametr |
| Tranzystancja przejściowa | Shunt | CCVS | y-Parametr | |
| Transkonduktancja | Seria | Seria | VCCS | z-.parametr |
| Voltage | Series | Shunt | VCVS | h-parametr |
Na przykład, dla wzmacniacza ze sprzężeniem zwrotnym prądowym, prąd z wyjścia jest próbkowany dla sprzężenia zwrotnego i łączony z prądem na wejściu. Dlatego sprzężenie zwrotne idealnie jest realizowane za pomocą (wyjściowego) źródła prądu sterowanego prądem (CCCS), a jego niedoskonała realizacja za pomocą sieci dwuportowej również musi zawierać CCCS, czyli odpowiednim wyborem dla sieci sprzężenia zwrotnego jest dwuport g-parametrowy. Tutaj przedstawiona jest metoda dwuportowa stosowana w większości podręczników, z wykorzystaniem układu traktowanego w artykule o asymptotycznym modelu wzmocnienia.

Rysunek 3 przedstawia dwutranzystorowy wzmacniacz z rezystorem sprzężenia zwrotnego Rf. Celem jest przeanalizowanie tego układu, aby znaleźć trzy elementy: wzmocnienie, impedancję wyjściową patrząc na wzmacniacz od strony obciążenia oraz impedancję wejściową patrząc na wzmacniacz od strony źródła.
- Zamiana sieci sprzężenia zwrotnego na dwuportowąEdit
- Obwód małosygnałowyEdit
- Obciążone wzmocnienie otwartej pętliEdit
- Wzmocnienie ze sprzężeniem zwrotnymEdit
- Rezystancje wejściowe i wyjścioweEdit
- Wprowadzenie do wyznaczania rezystancjiEdit
- Zastosowanie do przykładowego wzmacniaczaEdit
- Napięcie obciążenia i prąd obciążeniaEdit
- Czy blok wzmacniacza głównego jest dwuportowy?Edycja
Zamiana sieci sprzężenia zwrotnego na dwuportowąEdit
Pierwszym krokiem jest zamiana sieci sprzężenia zwrotnego na dwuportową. Tylko jakie elementy wchodzą w skład dwuportu?
Po stronie wejściowej dwuportu mamy Rf. Jeśli zmienia się napięcie po prawej stronie Rf, to zmienia się prąd w Rf, który jest odejmowany od prądu wchodzącego do bazy tranzystora wejściowego. Czyli strona wejściowa dwuportu jest zależnym źródłem prądowym sterowanym napięciem na wierzchołku rezystora R2.
Można powiedzieć, że drugi stopień wzmacniacza jest po prostu wtórnikiem napięciowym, przekazującym napięcie na kolektorze tranzystora wejściowego na wierzchołek R2. To znaczy, że monitorowany sygnał wyjściowy jest tak naprawdę napięciem na kolektorze tranzystora wejściowego. Ten pogląd jest uzasadniony, ale wtedy stopień wtórnika napięciowego staje się częścią sieci sprzężenia zwrotnego. To sprawia, że analiza sprzężenia zwrotnego staje się bardziej skomplikowana.
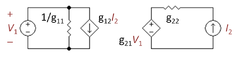
Alternatywny pogląd jest taki, że napięcie na szczycie R2 jest ustalane przez prąd emitera tranzystora wyjściowego. Ten pogląd prowadzi do całkowicie pasywnej sieci sprzężenia zwrotnego składającej się z R2 i Rf. Zmienną sterującą sprzężeniem zwrotnym jest prąd emitera, więc sprzężenie zwrotne jest źródłem prądowym (CCCS – current-controlled current source). Przeszukujemy cztery dostępne sieci dwuportowe i stwierdzamy, że jedyną siecią z CCCS jest dwuport g-parametrowy, pokazany na rysunku 4. Następnym zadaniem jest takie dobranie g-parametrów, aby dwuport z rysunku 4 był elektrycznie równoważny odcinkowi L złożonemu z R2 i Rf. Wybór ten jest procedurą algebraiczną dokonywaną najprościej poprzez rozpatrzenie dwóch indywidualnych przypadków: przypadek z V1 = 0, co powoduje, że VCVS po prawej stronie dwuportu jest zwarty; oraz przypadek z I2 = 0, co powoduje, że CCCS po lewej stronie jest obwodem otwartym. Algebra w tych dwóch przypadkach jest prosta, znacznie łatwiejsza niż rozwiązywanie dla wszystkich zmiennych naraz. Dobór g-parametrów, które powodują, że dwuport i sekcja L zachowują się tak samo, jest pokazany w poniższej tabeli.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {displaystyle {{frac {1}{R_{mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 + R f {displaystyle -{displaystyle {{frac {R_{2}}{R_{2}+R_{mathrm {f} }}}}
 |
R 2 R 2 + R f {{displaystyle {{frac {R_{2}}}{R_{2}+R_{mathrm {f} }}}}
 |
R 2 / / R f {displaystyle R_{2}//R_{mathrm {f} }\ }
 |
Obwód małosygnałowyEdit
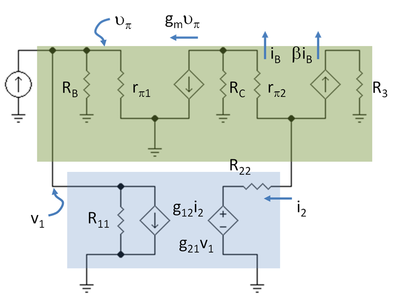
Kolejnym krokiem jest narysowanie schematu małosygnałowego dla wzmacniacza z założonym dwuportem z wykorzystaniem modelu hybrydowego-pi dla tranzystorów. Rysunek 5 przedstawia schemat z notacją R3 = RC2 // RL oraz R11 = 1 / g11, R22 = g22.
Obciążone wzmocnienie otwartej pętliEdit
Rysunek 3 wskazuje węzeł wyjściowy, ale nie wybór zmiennej wyjściowej. Przydatnym wyborem jest wyjście prądu zwarciowego wzmacniacza (prowadzące do wzmocnienia prądu zwarciowego). Ponieważ ta zmienna prowadzi po prostu do dowolnego z pozostałych wyborów (na przykład napięcia lub prądu obciążenia), wzmocnienie prądu zwarcia jest znajdowane poniżej.
Najpierw znajdowane jest wzmocnienie obciążonej pętli otwartej. Sprzężenie zwrotne jest wyłączane przez ustawienie g12 = g21 = 0. Chodzi o to, aby znaleźć, jak bardzo zmienia się wzmocnienie wzmacniacza z powodu samych rezystorów w sieci sprzężenia zwrotnego, przy wyłączonym sprzężeniu zwrotnym. To obliczenie jest dość proste, ponieważ R11, RB i rπ1 są równoległe, a v1 = vπ. Niech R1 = R11 // RB // rπ1. Dodatkowo, i2 = -(β+1) iB. Wynik dla wzmocnienia prądowego AOL w otwartej pętli wynosi:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . A_{displaystyle A_{mathrm {OL} }={frac {{beta i_{mathrm {B}} }}{i_{mathrm {S} }}=g_{m}R_{mathrm {C} }}} lewa strona({ {{frac {R_{1}}{R_{22}+{{frac {r_{pi 2}}+R_{mathrm {C}} }}{}{beta +1}}}}}right)}.

Wzmocnienie ze sprzężeniem zwrotnymEdit
W klasycznym podejściu do sprzężenia zwrotnego, feedforward reprezentowany przez VCVS (czyli g21 v1) jest zaniedbywany. To sprawia, że obwód z rysunku 5 przypomina schemat blokowy z rysunku 1, a wzmocnienie ze sprzężeniem zwrotnym wynosi wtedy:
A F B = A O L 1 + β F B A O L {displaystyle A_{athrm {FB} }={frac {A_{mathrm {OL} }}{1+{beta }_{mathrm {FB}}. } A_{mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {{displaystyle A_{mathrm {FB} }={frac {A_{mathrm {OL} }}{1+{frac {R_{2}}{R_{2}+R_{mathrm {f}} }}} A_{mathrm {OL} }}, }
Rezystancje wejściowe i wyjścioweEdit

Sprzężenie zwrotne jest wykorzystywane do lepszego dopasowania źródeł sygnału do ich obciążeń. Na przykład, bezpośrednie połączenie źródła napięcia z obciążeniem rezystancyjnym może spowodować utratę sygnału z powodu podziału napięcia, ale wprowadzenie wzmacniacza z ujemnym sprzężeniem zwrotnym może zwiększyć pozorne obciążenie widziane przez źródło i zmniejszyć pozorną impedancję sterownika widzianą przez obciążenie, unikając tłumienia sygnału z powodu podziału napięcia. Ta zaleta nie jest ograniczona do wzmacniaczy napięciowych, ale analogiczna poprawa dopasowania może być zastosowana we wzmacniaczach prądowych, wzmacniaczach transkonduktancyjnych i wzmacniaczach transrezystancyjnych.
Aby wyjaśnić te efekty sprzężenia zwrotnego na impedancjach, najpierw dygresja na temat tego, jak teoria dwóch portów podchodzi do określania rezystancji, a następnie jej zastosowanie do omawianego wzmacniacza.
Wprowadzenie do wyznaczania rezystancjiEdit
Rysunek 6 przedstawia układ równoważny do znajdowania rezystancji wejściowej wzmacniacza napięciowego ze sprzężeniem zwrotnym (po lewej) i wzmacniacza prądowego ze sprzężeniem zwrotnym (po prawej). Układy te są typowymi zastosowaniami twierdzenia Millera.
W przypadku wzmacniacza napięciowego, napięcie wyjściowe βVout sieci sprzężenia zwrotnego jest przyłożone szeregowo i z polaryzacją przeciwną do napięcia wejściowego Vx wędrującego przez pętlę (ale w odniesieniu do masy, polaryzacje są takie same). W wyniku tego napięcie skuteczne i prąd płynący przez rezystancję wejściową wzmacniacza Rin maleją, a więc rezystancja wejściowa obwodu rośnie (można powiedzieć, że Rin pozornie rośnie). Jego nową wartość można obliczyć stosując twierdzenie Millera (dla napięć) lub podstawowe prawa obwodów. I tak prawo napięciowe Kirchhoffa przewiduje:
V x = I x R i n + β v o u t , {displaystyle V_{x}=I_{x}R_{mathrm {w} }+beta v_{mathrm {out} }, }

gdzie vout = Av vin = Av Ix Rin. Podstawiając ten wynik do powyższego równania i rozwiązując dla rezystancji wejściowej wzmacniacza ze sprzężeniem zwrotnym, otrzymujemy:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . }(fb)={frac {V_{x}}{I_{x}}}=left(1+beta A_{v}}right)R_{mathrm {in} }\ .}

Ogólny wniosek z tego przykładu i podobnego przykładu dla przypadku rezystancji wyjściowej jest następujący:Szeregowe połączenie sprzężenia zwrotnego na wejściu (wyjściu) zwiększa rezystancję wejściową (wyjściową) o współczynnik ( 1 + β AOL ), gdzie AOL = wzmocnienie pętli otwartej.
Z drugiej strony, dla wzmacniacza prądowego, prąd wyjściowy βIout sieci sprzężenia zwrotnego jest przyłożony równolegle i z przeciwnym kierunkiem do prądu wejściowego Ix. W wyniku tego całkowity prąd płynący przez wejście obwodu (nie tylko przez rezystancję wejściową Rin) wzrasta, a napięcie na nim maleje, przez co maleje rezystancja wejściowa obwodu (Rin pozornie maleje). Jego nową wartość można obliczyć, stosując podwójne twierdzenie Millera (dla prądów) lub podstawowe prawa Kirchhoffa:
I x = V i n R i n + β i o u t . {I_{x}={frac {V_{mathrm {w} }}{R_{mathrm {in} {}}+beta i_{mathrm {out}} }\ .}

gdzie iout = Ai iin = Ai Vx / Rin. Podstawiając ten wynik do powyższego równania i rozwiązując dla rezystancji wejściowej wzmacniacza ze sprzężeniem zwrotnym, otrzymujemy:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . }(fb)={{frac {V_{x}}{I_{x}}}={{frac {R_{mathrm {in}} }}{}left(1+beta A_{i}}right)}}.

Ogólny wniosek z tego przykładu i podobnego przykładu dla przypadku rezystancji wyjściowej jest następujący:Połączenie równoległe ze sprzężeniem zwrotnym na wejściu (wyjściu) zmniejsza rezystancję wejściową (wyjściową) o współczynnik ( 1 + β AOL ), gdzie AOL = wzmocnienie pętli otwartej.
Wnioski te można uogólnić na przypadki z dowolnymi napędami Nortona lub Thévenina, dowolnymi obciążeniami i ogólnymi dwuportowymi sieciami sprzężenia zwrotnego. Jednakże, wyniki zależą od tego, czy wzmacniacz główny jest reprezentowany jako dwuportowy – to znaczy, wyniki zależą od tego, czy ten sam prąd wchodzi i wychodzi z zacisków wejściowych, i podobnie, ten sam prąd, który wychodzi z jednego zacisku wyjściowego, musi wchodzić do drugiego zacisku wyjściowego.
Szerzej sformułowany wniosek, niezależny od szczegółów ilościowych, jest taki, że sprzężenie zwrotne może być użyte do zwiększenia lub zmniejszenia impedancji wejściowej i wyjściowej.
Zastosowanie do przykładowego wzmacniaczaEdit
Wyniki dotyczące rezystancji są teraz zastosowane do wzmacniacza z rysunku 3 i rysunku 5. Współczynnik poprawy, który zmniejsza wzmocnienie, czyli ( 1 + βFB AOL), decyduje bezpośrednio o wpływie sprzężenia zwrotnego na rezystancje wejściową i wyjściową wzmacniacza. W przypadku połączenia bocznikowego impedancja wejściowa jest zmniejszana o ten współczynnik, a w przypadku połączenia szeregowego impedancja jest mnożona przez ten współczynnik. Jednakże impedancja, która jest modyfikowana przez sprzężenie zwrotne jest impedancją wzmacniacza z rysunku 5 z wyłączonym sprzężeniem zwrotnym i zawiera modyfikacje impedancji spowodowane przez rezystory sieci sprzężenia zwrotnego.
Więc impedancja wejściowa widziana przez źródło przy wyłączonym sprzężeniu zwrotnym wynosi Rin = R1 = R11 // RB // rπ1, a przy włączonym sprzężeniu zwrotnym (ale bez feedforward)
R i n = R 1 1 + β F B A O L , {displaystyle R_{mathrm {in} }={frac {R_{1}}{1+{beta }_{mathrm {FB}} } A_{mathrm {OL} }}, }
Impedancja widziana przez obciążenie wymaga dalszego omówienia. Obciążenie na rysunku 5 jest podłączone do kolektora tranzystora wyjściowego, a więc jest oddzielone od korpusu wzmacniacza nieskończoną impedancją wyjściowego źródła prądowego. Dlatego sprzężenie zwrotne nie ma żadnego wpływu na impedancję wyjściową, która pozostaje po prostu RC2, jak widać po rezystorze obciążenia RL na rysunku 3.
Jeśli zamiast tego chcielibyśmy znaleźć impedancję prezentowaną na emiterze tranzystora wyjściowego (zamiast jego kolektora), który jest szeregowo połączony z siecią sprzężenia zwrotnego, sprzężenie zwrotne zwiększyłoby tę rezystancję o współczynnik poprawy ( 1 + βFB AOL).
Napięcie obciążenia i prąd obciążeniaEdit
Wzmocnienie wyprowadzone powyżej jest wzmocnieniem prądu na kolektorze tranzystora wyjściowego. Aby odnieść to wzmocnienie do wzmocnienia, gdy napięcie jest wyjściem wzmacniacza, zauważ, że napięcie wyjściowe na obciążeniu RL jest związane z prądem kolektora przez prawo Ohma jako vL = iC (RC2 || RL). W związku z tym wzmocnienie transoporowe vL / iS znajdujemy mnożąc wzmocnienie prądowe przez RC2 || RL:
v L i S = A F B ( R C 2 ∥ R L ) . {displaystyle {frac {v_{mathrm {L} }}{i_{mathrm {S} }}=A_{mathrm {FB} }(R_{mathrm {C2} }} równoległe R_{mathrm {L}})}.

Podobnie, jeśli za wyjście wzmacniacza przyjmiemy prąd w rezystorze obciążenia RL, podział prądu wyznacza prąd obciążenia, a wzmocnienie wynosi wtedy:
i L i S = A F B R C 2 R C 2 + R L . {displaystyle {{frac {i_{mathrm {L}} }}{i_{mathrm {S} }}=A_{mathrm {FB} }}{R_{mathrm {C2}}. }}{R_{\\\\\\ {C2}} }+R_{mathrm {L} }}}\ .}

Czy blok wzmacniacza głównego jest dwuportowy?Edycja

Poniżej przedstawiono niektóre wady podejścia dwuportowego, przeznaczone dla uważnego czytelnika.
Rysunek 7 przedstawia schemat małosygnałowy z głównym wzmacniaczem i dwuportem sprzężenia zwrotnego w zacienionych polach. Dwuport ze sprzężeniem zwrotnym spełnia warunki portowe: na wejściu Iin wchodzi i wychodzi z portu i podobnie na wyjściu Iout wchodzi i wychodzi.
Czy blok wzmacniacza głównego jest również dwuportowy? Wzmacniacz główny jest pokazany w górnej zacienionej ramce. Połączenia masy są oznaczone. Rysunek 7 pokazuje interesujący fakt, że wzmacniacz główny nie spełnia warunków portu na wejściu i wyjściu, chyba że połączenia masy są tak dobrane, aby tak się stało. Na przykład, po stronie wejściowej, prąd wchodzący do wzmacniacza głównego to IS. Prąd ten jest dzielony na trzy sposoby: na sieć sprzężenia zwrotnego, na rezystor biasu RB i na rezystancję bazy tranzystora wejściowego rπ. Aby spełnić warunek portu wzmacniacza głównego, wszystkie trzy składowe muszą być zwrócone na stronę wejściową wzmacniacza głównego, co oznacza, że wszystkie wyprowadzenia masy oznaczone jako G1 muszą być połączone, podobnie jak wyprowadzenie emitera GE1. Analogicznie, po stronie wyjściowej należy podłączyć wszystkie masy oznaczone G2, a także masę GE2. Następnie, na dole schematu, pod dwuportem sprzężenia zwrotnego i poza blokami wzmacniacza, G1 jest połączone z G2. To wymusza podział prądów masy pomiędzy stronę wejściową i wyjściową zgodnie z planem. Zauważ, że taki układ połączeń dzieli emiter tranzystora wejściowego na stronę bazy i stronę kolektora – jest to fizycznie niemożliwe do zrobienia, ale elektrycznie układ widzi wszystkie połączenia masy jako jeden węzeł, więc taka fikcja jest dozwolona.
Oczywiście, sposób połączenia przewodów masy nie robi różnicy dla wzmacniacza (wszystkie są jednym węzłem), ale robi różnicę dla warunków portu. Ta sztuczność jest słabością tego podejścia: warunki portu są potrzebne do uzasadnienia metody, ale na obwód naprawdę nie ma wpływu to, jak prądy są wymieniane pomiędzy połączeniami masy.
Jednakże, jeśli żaden możliwy układ uziemienia nie prowadzi do warunków portu, obwód może nie zachowywać się w ten sam sposób. Współczynniki poprawy (1 + βFB AOL) dla określenia impedancji wejściowej i wyjściowej mogą nie działać. Taka sytuacja jest kłopotliwa, ponieważ niepowodzenie w wykonaniu dwuportu może odzwierciedlać rzeczywisty problem (po prostu nie jest to możliwe), lub odzwierciedlać brak wyobraźni (na przykład, po prostu nie pomyślano o podzieleniu węzła emitera na dwie części). W konsekwencji, gdy warunki portu są wątpliwe, możliwe są co najmniej dwa podejścia do ustalenia, czy współczynniki poprawy są dokładne: albo symulacja przykładu przy użyciu Spice i porównanie wyników z użyciem współczynnika poprawy, albo obliczenie impedancji przy użyciu źródła testowego i porównanie wyników.
Bardziej praktycznym wyborem jest całkowite porzucenie podejścia dwuportowego i użycie różnych alternatyw opartych na teorii grafu przepływu sygnału, w tym metody Rosenstark, metody Choma i użycie twierdzenia Blackmana. Ten wybór może być zalecany, jeśli małosygnałowe modele urządzeń są złożone lub nie są dostępne (na przykład, urządzenia są znane tylko numerycznie, być może z pomiarów lub z symulacji SPICE).