W samouczku uogólnionych modeli liniowych, dowiedzieliśmy się o różnych GLM’s jak regresja liniowa, regresja logistyczna, itp. W tym tutorialu z serii TechVidvan’s R tutorial, zamierzamy przyjrzeć się regresji liniowej w R w szczegółach. Dowiemy się, czym jest regresja liniowa w R i jak ją zaimplementować w R. Przyjrzymy się metodzie estymacji najmniejszych kwadratów, a także dowiemy się, jak sprawdzić dokładność modelu.

Więc, bez dalszych ceregieli, zaczynajmy!

Regresja liniowa w R

Regresja liniowa w R jest metodą używaną do przewidywania wartości zmiennej przy użyciu wartości jednej lub więcej zmiennych wejściowych. Celem regresji liniowej jest ustalenie liniowej zależności między pożądaną zmienną wyjściową a predykatorami wejściowymi.

Modelowanie zmiennej ciągłej Y jako funkcji jednej lub więcej wejściowych zmiennych predykatora Xi, tak aby funkcja mogła być użyta do przewidywania wartości Y, gdy znane są tylko wartości Xi. Ogólna postać takiej liniowej zależności to:

Y=?0+?1 X

Tutaj ?0 jest przechwytem
i ?1 jest nachyleniem.

Typy regresji liniowej w R

Istnieją dwa typy regresji liniowej w R:

• Simple Linear Regression
• Multiple Linear Regression

Przyjrzyjrzyjrzyjmy się im po kolei.

Prosta regresja liniowa w R

Prosta regresja liniowa ma na celu znalezienie liniowej zależności między dwiema ciągłymi zmiennymi. Należy zauważyć, że związek ten ma charakter statystyczny, a nie deterministyczny.

Związek deterministyczny to taki, w którym wartość jednej zmiennej można znaleźć dokładnie za pomocą wartości drugiej zmiennej. Przykładem związku deterministycznego jest związek między kilometrami i milami. Używając wartości kilometra, możemy dokładnie znaleźć odległość w milach. Zależność statystyczna nie jest dokładna i zawsze obarczona jest błędem przewidywania. Na przykład, mając wystarczającą ilość danych, możemy znaleźć związek między wzrostem i wagą osoby, ale zawsze będzie margines błędu i będą istniały wyjątkowe przypadki.

Ideą prostej regresji liniowej jest znalezienie linii, która najlepiej pasuje do danych wartości obu zmiennych. Ta linia może następnie pomóc nam znaleźć wartości zmiennej zależnej, gdy ich brakuje.

Zbadajmy to z pomocą przykładu. Mamy zbiór danych składający się z wysokości i wagi 500 osób. Naszym celem jest zbudowanie modelu regresji liniowej, który formułuje zależność pomiędzy wzrostem i wagą, tak, że gdy podamy wzrost(Y) jako dane wejściowe do modelu, może on podać wagę(X) w zamian z minimalnym marginesem błędu.

Y=b0+b1X

Wartości b0 i b1 powinny być tak dobrane, aby minimalizowały margines błędu. Metryka błędu może być użyta do pomiaru dokładności modelu.

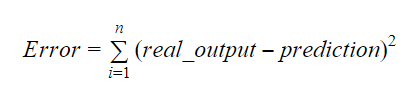
Możemy obliczyć nachylenie lub współczynnik jako: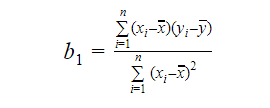

Wartość b1 daje nam wgląd w charakter związku pomiędzy zmienną zależną i niezależną.

• Jeśli b1 > 0, to zmienne mają związek dodatni tzn. wzrost x spowoduje wzrost y.
• Jeśli b1 < 0, to zmienne mają relację ujemną tzn. wzrost x spowoduje spadek y.

Wartość b0 lub intercept można obliczyć w następujący sposób: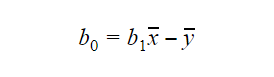
Wartość b0 może również dać wiele informacji o modelu i odwrotnie.

Jeśli model nie zawiera x=0, to predykcja jest bezsensowna bez b1. Aby model miał tylko b0, a nie b1 w nim w dowolnym punkcie, wartość x musi być 0 w tym punkcie. W przypadkach takich jak wzrost, x nie może być 0 i wzrost osoby nie może być 0. Dlatego taki model jest bezsensowny z tylko b0.

Jeśli brakuje terminu b0, wtedy model przejdzie przez początek, co będzie oznaczać, że predykcja i współczynnik regresji (nachylenie) będą nieobiektywne.

Multiple Linear Regression in R

Multiple linear regression jest rozszerzeniem prostej regresji liniowej. W regresji liniowej wielokrotnej dążymy do stworzenia modelu liniowego, który może przewidzieć wartość zmiennej docelowej przy użyciu wartości wielu zmiennych predykcyjnych. Ogólna postać takiej funkcji jest następująca:

Y=b0+b1X1+b2X2+…+bnXn

Ocena dokładności modelu

Istnieją różne metody oceny jakości i dokładności modelu. Przyjrzyjmy się niektórym z tych metod po kolei.

R-Squared

Prawdziwą informacją w danych jest wariancja w nich zawarta. R-kwadrat mówi nam, jaka część wariancji w zmiennej docelowej (y) jest wyjaśniona przez model. Możemy znaleźć miarę R-squared modelu używając następującego wzoru: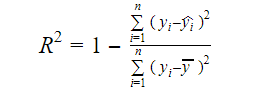

Gdzie,

• yi jest dopasowaną wartością y dla obserwacji i
• y jest średnią Y.

Niższa wartość R-squared oznacza mniejszą dokładność modelu. Jednak miara R-kwadrat nie musi być ostatecznym czynnikiem decydującym.

Skorygowany R-kwadrat

Jak wzrasta liczba zmiennych w modelu, wzrasta również wartość R-kwadrat. Powoduje to również błędy w zmienności objaśnianej przez nowo dodane zmienne. Dlatego dostosowujemy wzór na R kwadrat dla wielu zmiennych.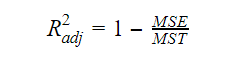
Tutaj MSE oznacza Średni Błąd Standardowy, który wynosi:

I MST oznacza Średnią Sumę Standardową, która wynosi: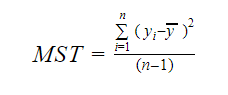

Gdzie, n jest liczbą obserwacji, a q jest liczbą współczynników.

Zależność między R-squared i skorygowanym R-squared jest: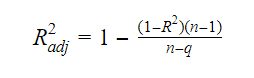

Błąd standardowy i F-statystyka

Błąd standardowy i F-statystyka są miarami jakości dopasowania modelu. Wzory na błąd standardowy i statystykę F to:

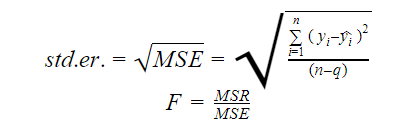
Gdzie MSR oznacza Mean Square Regression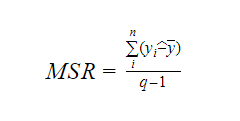

AIC i BIC

Kryterium informacyjne Akaike’a i bayesowskie kryterium informacyjne są miarami jakości dopasowania modeli statystycznych. Mogą być również stosowane jako kryteria wyboru modelu.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Gdzie,

• L jest funkcją prawdopodobieństwa,
• k jest liczbą parametrów modelu,
• n jest wielkością próby.

funkcja lm w R

Funkcja lm() w R dopasowuje modele liniowe. Może ona przeprowadzać regresję oraz analizę wariancji i kowariancji. Składnia funkcji lm jest następująca:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Gdzie,

• formuła jest obiektem klasy „formuła” i jest symboliczną reprezentacją modelu do dopasowania,
• dane są ramką danych lub listą, która zawiera zmienne w formule(dane są opcjonalnym argumentem. Jeśli go brakuje, funkcja pobiera zmienne ze środowiska),
• subset jest opcjonalnym wektorem zawierającym podzbiór obserwacji, które mają być użyte w procesie dopasowania,
• weights jest opcjonalnym wektorem określającym wagi, które mają być użyte w procesie dopasowania,
• na.action jest funkcją, która pokazuje, co powinno się stać, gdy NA są napotkane w danych,
• method oznacza metodę dopasowania modelu,
• model, x, y, i qr są logikami, które kontrolują, czy odpowiednie wartości powinny być zwrócone z wyjściem, czy nie. Wartości te są następujące:
• model: ramka modelu
• x: macierz modelu
• y: odpowiedź
• qr: rozkład qr
• singular.ok jest logiką, która kontroluje, czy dozwolone są dopasowania singularne czy nie,
• offset jest wcześniej znanym predyktorem, który powinien być użyty w modelu,
• . . są dodatkowymi argumentami, które należy przekazać do funkcji regresji niższego poziomu.

Praktyczny przykład regresji liniowej w R

Na razie wystarczy teorii. Przyjrzyjmy się, jak to wszystko zaimplementować. Zamierzamy dopasować model liniowy używając regresji liniowej w R z pomocą funkcji lm(). Później sprawdzimy również jakość dopasowania modelu. Wykorzystajmy zbiór danych samochodów, który jest domyślnie dostarczany w podstawowym pakiecie R.

1. Zacznijmy od graficznej analizy zbioru danych, aby lepiej się z nim zapoznać. W tym celu narysujemy wykres rozrzutu i sprawdzimy, co mówi nam on o danych.

Możemy użyć funkcji scatter.smooth(), aby utworzyć wykres rozrzutu dla zbioru danych.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Wyjście

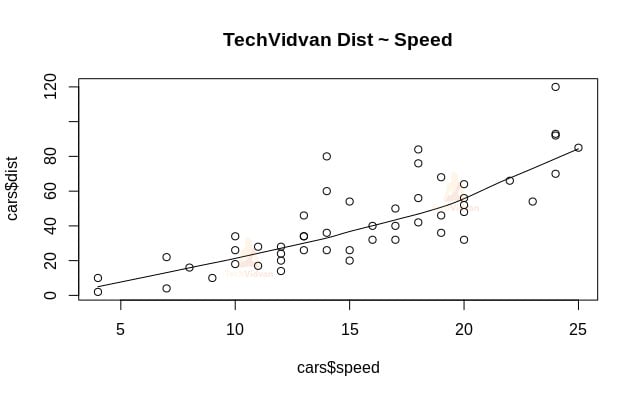
Wykres rozrzutu pokazuje nam dodatnią korelację między odległością a prędkością. Sugeruje to liniowo rosnący związek między tymi dwiema zmiennymi. To sprawia, że dane są odpowiednie dla regresji liniowej, ponieważ liniowa zależność jest podstawowym założeniem przy dopasowywaniu modelu liniowego do danych.

2. Teraz, gdy sprawdziliśmy, że regresja liniowa jest odpowiednia dla danych, możemy użyć funkcji lm(), aby dopasować do nich model liniowy.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Wyjście

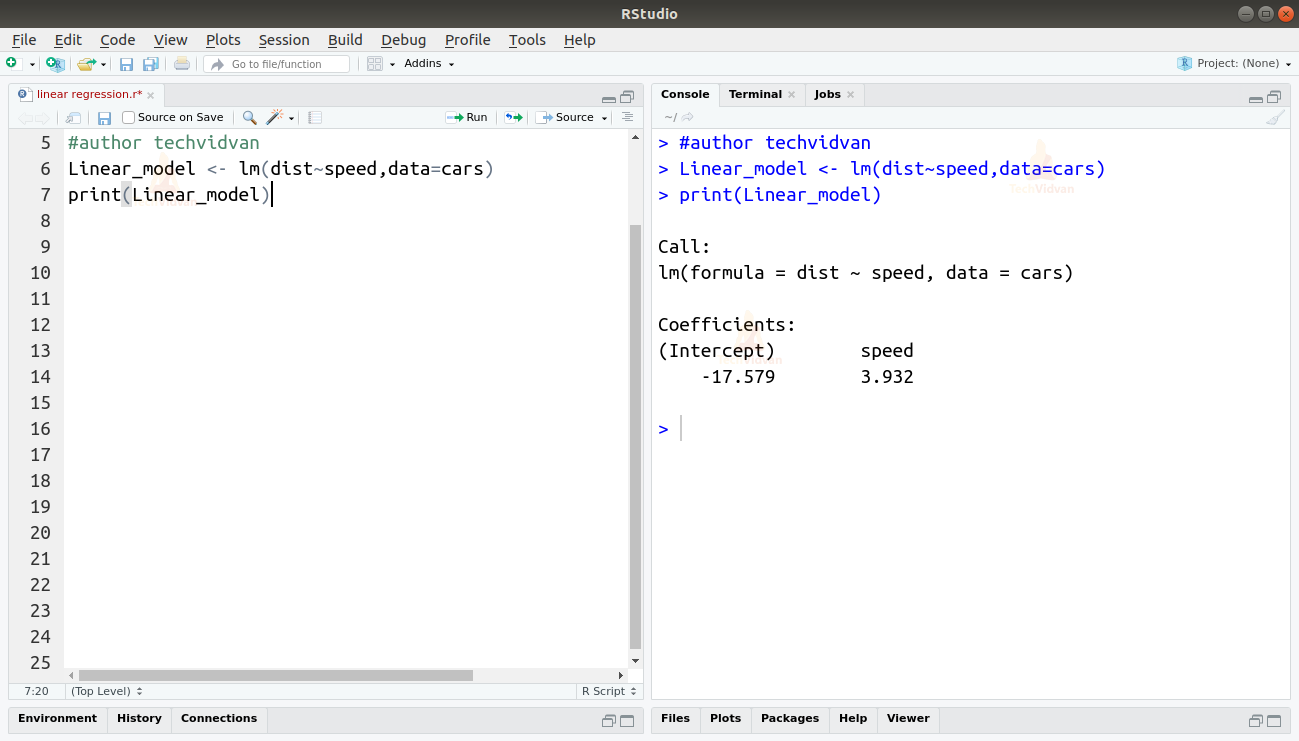
Wyjście funkcji lm() pokazuje nam intercept i współczynnik prędkości. W ten sposób definiujemy liniową zależność między odległością a prędkością jako:

Dystans=pochodna+współczynnik*prędkość

Dystans=-17.579+3.932*prędkość

3. Teraz, gdy dopasowaliśmy model sprawdźmy jakość lub dobroć dopasowania. Zacznijmy od sprawdzenia podsumowania modelu liniowego za pomocą funkcji summary().

summary(Linear_model)

Wyjście

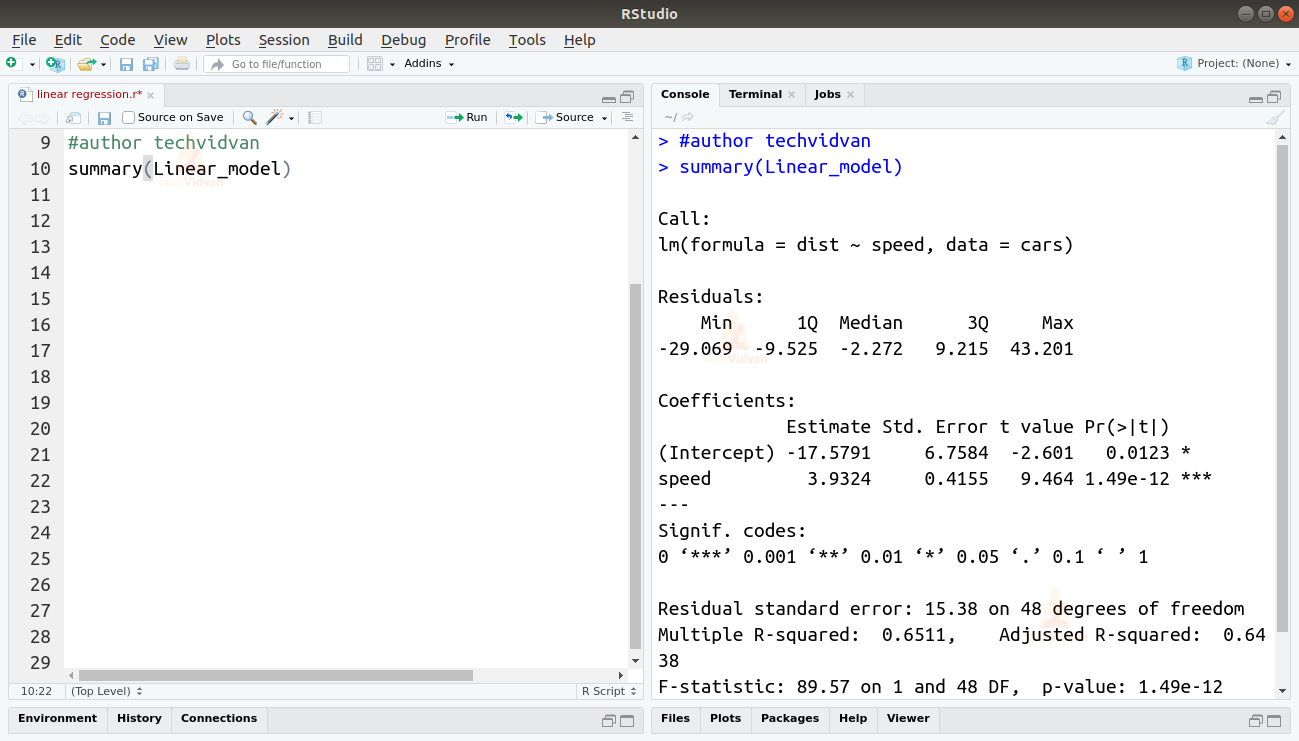
Funkcja summary() daje nam kilka ważnych miar, które pomagają zdiagnozować dopasowanie modelu. Wartość p-value jest ważną miarą dobroci dopasowania modelu. Mówi się, że model nie jest dopasowany, jeśli wartość p jest większa niż wcześniej ustalony poziom istotności statystycznej, który idealnie wynosi 0.05.

Podsumowanie dostarcza nam również wartość t. Im większa wartość t, tym lepsze dopasowanie modelu.
Możemy również znaleźć AIC i BIC używając funkcji AIC() i BIC().

AIC(Linear_model)BIC(Linear_model)

Wyjście

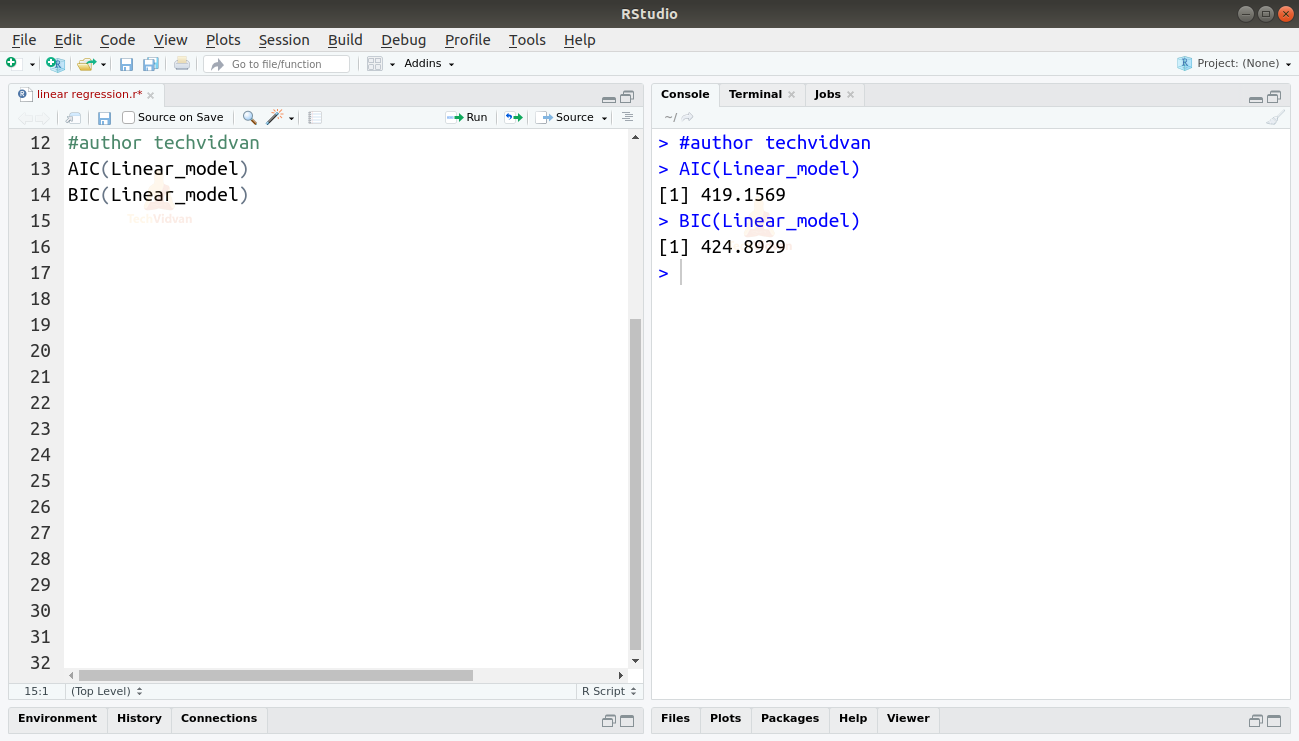
Model, który daje najniższe wyniki AIC i BIC, jest najbardziej preferowany.

Podsumowanie

W tym rozdziale serii samouczków TechVidvana w R poznaliśmy regresję liniową. Dowiedzieliśmy się o prostej regresji liniowej i wielokrotnej regresji liniowej. Następnie studiowaliśmy różne środki do oceny jakości lub dokładności modelu, takie jak R2, dostosowane R2, błąd standardowy, statystyka F, AIC i BIC. Następnie dowiedzieliśmy się jak zaimplementować regresję liniową w R. Następnie sprawdziliśmy jakość dopasowania modelu w R.

Do share your rating on Google if you liked the Linear Regression tutorial.