W lodach małe okrągłe kryształki lodu są ważne dla miękkiej i kremowej tekstury. Ogólnie rzecz biorąc, im szybsze jest zamrażanie, tym mniejszy jest rozmiar kryształów lodu. Jednak dla niektórych materiałów spożywczych istnieje górna granica szybkości zamrażania. Jeśli zamrażanie jest zbyt szybkie, w materiale spożywczym powstają naprężenia mechaniczne i może dojść do pęknięcia lodu. W kilku przypadkach proces zamrażania jest wykorzystywany do nadawania struktury materiałom, takim jak tradycyjne japońskie naczynie kori-tofu lub rusztowania stosowane w biologicznej inżynierii tkankowej. Kilka lat temu WUR, wraz z TU Delft i Unilever, badał zastosowanie liofilizacji do strukturyzacji warzyw na zupę. W tym przypadku wielkość kryształów lodu określa wielkość przestrzeni porowej po wysuszeniu i pomaga w rehydratacji warzyw po zmieszaniu z zupą.
Zależność między wielkością kryształów lodu a szybkością zamrażania
W związku z tym, z perspektywy jakości mrożonej żywności, ważne jest posiadanie dobrej wiedzy na temat zależności między wielkością kryształów lodu a szybkością zamrażania. Istnieją jednak tylko pewne empiryczne zależności pomiędzy szybkością zamrażania a wielkością kryształów lodu. Ponadto, w przypadku produkowanej żywności istnieją inne środki stosowane do kontroli wielkości kryształów lodu, takie jak kriopektanty, takie jak cukry i białka zapobiegające zamarzaniu. To wskazuje, że można oczekiwać interakcji pomiędzy składem materiału żywnościowego, szybkością zamrażania i wielkością kryształów lodu, jednak w empirycznych zależnościach zależność od składu żywności jest nieobecna. Dlatego Food & Biobased Research zaangażował się w projekt badawczy ukierunkowany na bardziej teoretyczne zrozumienie zależności pomiędzy szybkością zamrażania, składem i wielkością kryształów lodu przy użyciu zaawansowanych symulacji komputerowych.
Model pola fazowego dla wzrostu kryształów lodu
Aby uzyskać tak szczegółowe zrozumienie musimy zanurzyć się w mikrometrowy zakres mikrostruktury żywności, gdzie pojedyncze kryształy lodu są rozwiązywane w opracowanym modelu komputerowym, gdzie wzrost kryształów jest modelowany jako funkcja składu matrycy. Najbardziej zaawansowaną metodą w tej dziedzinie jest model pola fazowego, który wykorzystaliśmy do opisu struktury dyspersji takich jak piany i emulsje, stabilizowane emulgatorami. W metodzie pola fazowego można jednocześnie modelować kilka pojedynczych elementów dyspersji, takich jak krople emulsji, pęcherzyki piany i kryształy. Metoda łatwo pozwala na rozpad i koalescencję tych zdyspergowanych elementów.
Siła metody leży w sposobie traktowania interfejsu pomiędzy fazami zdyspergowaną i ciągłą. Metoda ta podąża za propozycją słynnego holenderskiego fizyka, VanderWaalsa, aby włączyć interfejs w ramy termodynamiczne. Wykorzystując metodę pola fazowego skonstruowaliśmy model komputerowy do opisu kryształów lodu w roztworze sacharozy, którego zachowanie może być postrzegane jako reprezentatywne dla lodów3. We wcześniejszych badaniach wyjaśniliśmy już termodynamikę wodnych roztworów sacharozy4, a także szybkość transportu wody w roztworze cukru na drodze dyfuzji5. Tak więc, dla tych właściwości materiału mamy dostępne teorie predykcyjne w funkcji stężenia sacharozy dla całego zakresu od 0 do 100%.
Szybkość zamrażania, skład i wielkość kryształów lodu
Po opracowaniu modelu komputerowego, przeprowadziliśmy kilka symulacji komputerowych w celu zbadania zależności pomiędzy szybkością zamrażania, składem i wielkością kryształów lodu. Zbliżyliśmy niewielką część materiału żywnościowego i zasialiśmy kilka jąder wzrostu kryształów lodu. Ta część materiału była następnie poddawana różnym szybkościom zamrażania. Symulacje zostały przeprowadzone dla dwóch różnych stężeń sacharozy – i wielu różnych losowych pozycji jąder – w celu uzyskania dobrych statystyk.
Zrzuty z tych symulacji komputerowych są pokazane na Rysunku 1. Ciemnoniebieskie rozproszone elementy to pojedyncze kryształki lodu. Szybkość zamrażania nie jest zbyt duża, więc możemy założyć, że kryształy lodu pozostają w przybliżeniu kuliste. Dla zrozumienia wyników symulacji ważne jest, aby wiedzieć, że kryształy lodu nie zawierają cukru, więc wzrost kryształów lodu implikuje wzrost stężenia cukru w fazie niezamarzniętej. Wzrost stężenia cukru prowadzi do podwyższenia temperatury zamarzania, pozostawiając ciągłą matrycę niezamarzniętą.

Rysunek 1: Migawki wzrostu kryształów lodu w roztworze cukru otrzymane poprzez symulacje komputerowe dla różnych szybkości zamrażania (0.01, 0.03 i 0.10 K/s od góry do dołu) obserwowane w różnym czasie (od lewej do prawej). Zauważ koalescencję kilku kryształów lodu, szczególnie przy niskiej szybkości zamrażania (góra)
Przy dalszym zamrażaniu kryształy lodu mogą na siebie napierać, powodując wzrost stężenia cukru w niezamarzniętej cieczy pomiędzy nimi, co prowadzi do obniżenia punktu zamarzania. W ten sposób powstaje płaski interfejs. Jeśli tempo zamrażania jest zbyt wolne, cukry mają czas na dyfuzję ze strefy zderzenia i kryształy mogą ulec koalescencji. We wczesnym etapie zamrażania, gdy lokalny wzrost stężenia cukru spowodowany wzrostem kryształów lodu jest niewielki, dochodzi do kilku zdarzeń koalescencji. W późniejszym etapie zamrażania niezamrożona matryca zbliża się do stanu szklistego – gdzie dyfuzja wody i cukru ulega zatrzymaniu, a wzrost kryształów lodu ustaje.
Na podstawie symulacji określiliśmy średni rozmiar kryształów lodu i wykreśliliśmy go względem narzuconej szybkości zamrażania dla dwóch różnych stężeń sacharozy. Wyniki te są przedstawione na Rysunku 2.
W danych symulacyjnych można zaobserwować znaczny rozrzut, spowodowany stochastycznością procesu nukleacji. Jednakże, wykonując wiele przebiegów symulacji, można dopasować wiarygodną zależność potęgową do danych, które są wyświetlane jako linie biegnące przez punkty danych na Rysunku 2 (strona 00). Dopasowanie pokazuje, że wykładniki prawa potęgowego wynoszą 0,31 i 0,18 odpowiednio dla 10% i 15% początkowego stężenia cukru. Nasza wcześniejsza zależność empiryczna ma wykładnik prawa potęgowego równy 0,25, który był zakładany jako niezależny od składu. Fakt, że wartość empiryczna jest dość bliska wykładnikom, które znaleźliśmy w wyniku symulacji, jest bardzo zachęcający. Ponadto, warto zauważyć, że model symulacyjny nie wymagał żadnego dopasowania parametrów, ponieważ wszystkie właściwości materiałowe i termodynamiczne są znane.
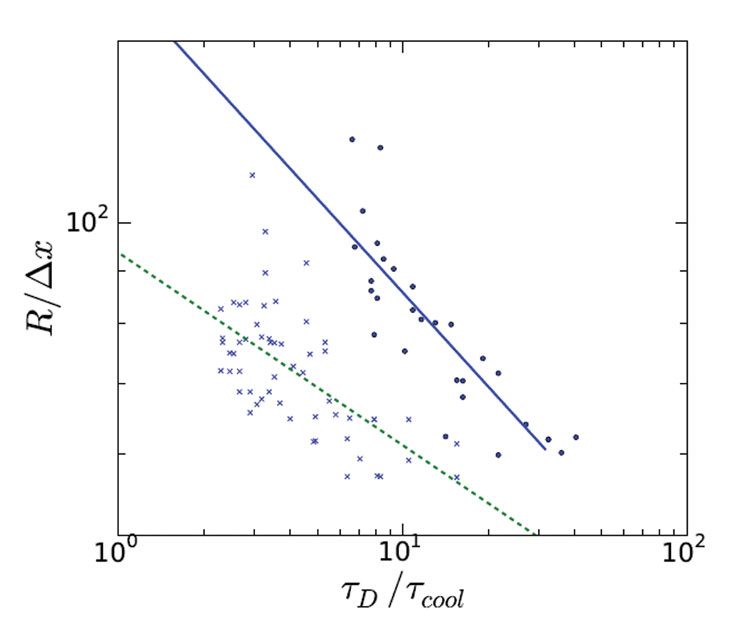
Rysunek 2: Średni rozmiar kryształu lodu w zależności od szybkości zamrażania, dla dwóch różnych początkowych stężeń cukru (10% i 15%, oznaczone linią ciągłą i przerywaną). Promień jest mierzony w jednostkach siatki obliczeniowej, która wynosi około 3 mikronów, a szybkość zamrażania 1/tcool jest mierzona w kategoriach szybkości dyfuzji wody 1/tD. (przy 0.01K/s jeśli tD/tcool=1) Punkty wskazują średnią wielkość pojedynczej symulacji. Linie reprezentują relacje prawa potęgowego, dopasowane do danych symulacyjnych
Kwestie jakości mrożonych owoców i warzyw
Żywność & Biobased Research konkluduje, że model ma duży stopień realizmu. Co więcej, podobne teorie predykcyjne dotyczące właściwości materiałowych i termodynamicznych są dostępne dla wielu innych materiałów spożywczych. W związku z tym model ten można w zasadzie zastosować do wielu innych materiałów spożywczych. Na tej podstawie rozpoczęliśmy nowy projekt badawczy, który kontynuuje rozwój i adaptację modelu do mrożonych materiałów spożywczych o strukturze komórkowej w celu zbadania kwestii jakości mrożonych owoców i warzyw. Model pola fazowego będzie osadzony w modelu wieloskalowym – ponieważ w produktach spożywczych powstają lokalne różnice w szybkości zamrażania – które muszą być rozwiązane za pomocą zaawansowanego podejścia, w którym profil temperatury jest obliczany w skali produktu, a wzrost kryształów lodu w skali mikro. Model komputerowy w skali makro będzie wielokrotnie wywoływał model w skali mikro dla wielu lokalizacji. Model mikroskalowy przekaże z powrotem lokalną frakcję lodu, podczas gdy model makroskalowy przekaże zastosowany gradient temperatury do modelu mikroskalowego.
W tym nowym projekcie, Food & Biobased Research, skupimy się nie tylko na początkowym etapie zamrażania, ale również na przechowywaniu mrożonek. Podczas przechowywania mogą wystąpić wahania temperatury z powodu mechanicznego chłodzenia lub otwierania i zamykania drzwi. Zakłada się, że te wahania temperatury umożliwiają dalszy wzrost kryształków lodu, co jest niekorzystne dla jakości produktu6. Naszym celem jest zbadanie, czy obniżenie temperatury przechowywania sprawia, że żywność jest mniej wrażliwa na wahania temperatury, a nawet czy można uzyskać zmniejszenie zużycia energii. Co więcej, nawet jeśli temperatura przechowywania jest w miarę stała, podczas przechowywania w konwencjonalnych warunkach -18oC nadal występuje zjawisko rozdrobnienia kryształów lodu. Pokazuje to porównanie żywności zamrożonej poprzez zamrażanie z podmuchem powietrza i zamrażanie z przesunięciem ciśnienia (PSF). Początkowo wielkość kryształów lodu uzyskanych za pomocą PSF jest znacznie mniejsza niż w przypadku konwencjonalnego zamrażania przez wydmuchiwanie powietrza. Jednak po kilku tygodniach przechowywania stwierdza się niewielką różnicę w ostatecznym rozkładzie wielkości kryształów lodu, co wskazuje na to, że podczas przechowywania żywności PSF doszło do zgrubienia7.
Podsumowując, nowy model symulacyjny jest niezbędnym narzędziem do zbadania możliwych sposobów kontroli tekstury mrożonej żywności i wielkości kryształów lodu przez przemysł mrożonek, w takich obszarach jak 1) formuła produktu, 2) warunki przetwarzania i szybkość zamrażania. Znając wpływ receptury i przetwarzania na jakość mrożonej żywności, można ocenić nowe strategie przechowywania mrożonek ze względu na ich wpływ zarówno na jakość produktu, jak i oszczędność energii.
- Voda, A., Homan, N., Witek, M., Duijster, A., van Dalen, G., van der Sman, R., Nijsse, J, van Vliet, L. Van As, H. & van Duynhoven, J. (2012). The impact of freeze-drying on microstructure and rehydration properties of carrot. Food Research International, 49(2), 687-693
- van der Sman, R. G. M., Voda, A., van Dalen, G., & Duijster, A. (2013). Interspacing kryształów lodu w mrożonej żywności. Journal of Food Engineering, 116(2), 622-626
- van der Sman, R. G. M. (2016). Phase field simulations of ice crystal growth in sugar solutions (Symulacje pola fazowego wzrostu kryształów lodu w roztworach cukru). International Journal of Heat and Mass Transfer, 95, 153-161
- van der Sman, R. G. M., & Meinders, M. B. J. (2011). Prediction of the state diagram of starch water mixtures using the Flory-Huggins free volume theory. Soft Matter, 7(2), 429-442
- van der Sman, R. G. M., & Meinders, M. B. J. (2013). Dyfuzyjność wilgoci w materiałach spożywczych. Food chemistry, 138(2), 1265-1274
- Regand, A & Goff HD. „Struktura i rekrystalizacja lodu w zamrożonych stabilizowanych systemach modelowych lodów”. Food Hydrocolloids1 (2003): 95-102
- Fernández PP, Otero L, Martino MM ,Molina-García AD, & Sanz PD „High-pressure shift freezing: recrystallization during storage” European Food Research and Technology 5 (2008): 1367-1377
O autorze
Ruud van der Sman posiada tytuł magistra fizyki stosowanej na Uniwersytecie Technicznym w Delft oraz tytuł doktora inżynierii rolniczej na Uniwersytecie Wageningen. Pracuje jako starszy badacz w Food & Biobased Research, a w niepełnym wymiarze godzin jako asystent profesora w Food Process Engineering – obie części Wageningen UR (University & Research Centre). Jego zainteresowania badawcze obejmują fizykę miękkiej materii materiałów spożywczych, modelowanie komputerowe struktury żywności w skali mikrometrów oraz modelowanie fizjologii. Jego doświadczenie w dziedzinie mięsa obejmuje termodynamikę zdolności zatrzymywania wody, wymianę ciepła i masy oraz fizjologię poubojową. www.wageningenur.nl/en/fbr