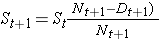Często jesteśmy zainteresowani oceną, czy istnieją różnice w przeżywalności (lub skumulowanej częstości występowania zdarzeń) pomiędzy różnymi grupami uczestników. Na przykład, w badaniu klinicznym z wynikiem przeżycia, możemy być zainteresowani porównaniem przeżycia pomiędzy uczestnikami otrzymującymi nowy lek w porównaniu do placebo (lub standardowej terapii). W badaniu obserwacyjnym może nas interesować porównanie przeżywalności między mężczyznami i kobietami lub między uczestnikami z określonym czynnikiem ryzyka (np. nadciśnieniem lub cukrzycą) i bez niego. Istnieje kilka dostępnych testów do porównywania przeżycia wśród niezależnych grup.

Test rang log

Test rang log jest popularnym testem do testowania hipotezy zerowej o braku różnicy w przeżyciu między dwiema lub więcej niezależnymi grupami. Test porównuje całe przeżycie między grupami i można o nim myśleć jako o teście, czy krzywe przeżycia są identyczne (nakładają się) czy nie. Krzywe przeżycia są szacowane dla każdej grupy, rozpatrywanej oddzielnie, za pomocą metody Kaplana-Meiera i porównywane statystycznie za pomocą testu log rank. Należy zwrócić uwagę, że istnieje kilka odmian statystyki log rank test, które są implementowane przez różne pakiety do obliczeń statystycznych (np. SAS, R 4,6). Przedstawiamy tutaj jedną wersję, która jest ściśle powiązana ze statystyką testu chi kwadrat i porównuje zaobserwowane do oczekiwanych liczby zdarzeń w każdym punkcie czasowym w okresie obserwacji.

Przykład:

Małe badanie kliniczne jest prowadzone w celu porównania dwóch terapii skojarzonych u pacjentów z zaawansowanym rakiem żołądka. Dwudziestu uczestników z rakiem żołądka w stadium IV, którzy wyrazili zgodę na udział w badaniu, zostaje losowo przydzielonych do otrzymywania chemioterapii przed operacją lub chemioterapii po operacji. Pierwszorzędowym wynikiem badania jest zgon, a uczestnicy są obserwowani przez okres do 48 miesięcy (4 lata) po włączeniu do badania. Doświadczenia uczestników w każdym ramieniu badania są przedstawione poniżej.

.

Chemoterapia przed operacją			Chemoterapia po operacji
Miesiąc Zgonu	Miesiąc ostatniego kontaktu		Miesiąc zgonu	Miesiąc ostatniego kontaktu
8	8		33	48
12	32		28	48
26	20		41	25
14	40			37
21				48
27				25
				43

Sześciu uczestników w grupie otrzymującej chemioterapię przed zabiegiem operacyjnym zmarło w trakcie obserwacji w porównaniu z trzema uczestnikami w grupie otrzymującej chemioterapię przed zabiegiem operacyjnym.w porównaniu z trzema uczestnikami w grupie otrzymującej chemioterapię po operacji. Pozostali uczestnicy w każdej grupie są obserwowani przez różną liczbę miesięcy, niektórzy aż do końca badania w wieku 48 miesięcy (w grupie chemioterapii po operacji). Korzystając z procedur opisanych powyżej, najpierw konstruujemy tablice trwania życia dla każdej grupy leczenia przy użyciu podejścia Kaplana-Meiera.

Tabela życia dla grupy otrzymującej chemioterapię przed operacją

.

Czas, Months	Liczba osób zagrożonych Nt	Liczba zgonów Dt	Liczba ocenzurowanych Ct	Prawdopodobieństwo przeżycia
0	10			1
8	10	1	1	0.900
12	8	1		0.788
14	7	1		0.675
20	6		1	0.675
21	5	1		0.540
26	4	1		0.405
27	3	1		0.270
32	2		1	0.270
40	1		1	0.270

Life Table for Group Receiving Chemotherapy After Surgery

.

Czas, Months	Liczba osób zagrożonych Nt	Liczba zgonów Dt	Liczba ocenzurowanych Ct	Prawdopodobieństwo przeżycia
0	10			1
25	10		2	1.000
28	8	1		0.875
33	7	1		0.750
37	6		1	0.750
41	5	1		0.600
43	4		1	0.600
48	3		3	0,600

Dwie krzywe przeżycia przedstawiono poniżej.

Survival in Each Treatment Group

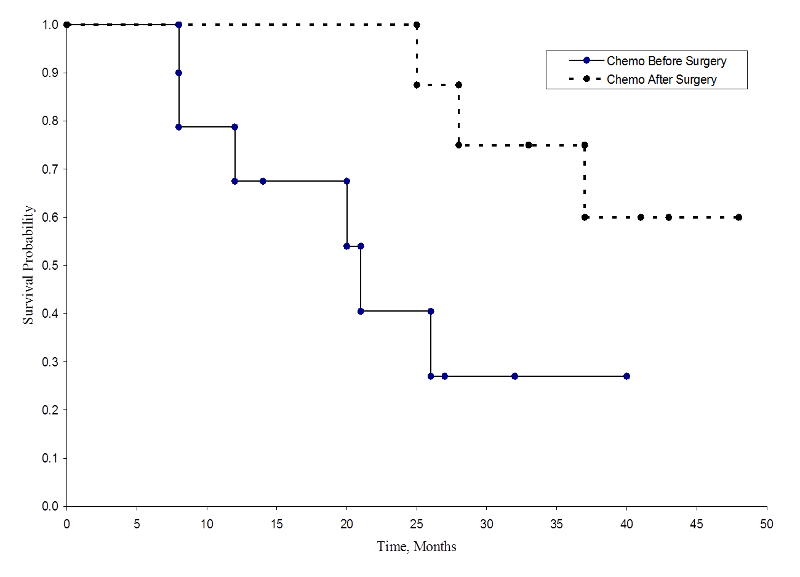
Prawdopodobieństwa przeżycia dla grupy otrzymującej chemioterapię po operacji są wyższe niż prawdopodobieństwa przeżycia dla grupy otrzymującej chemioterapię przed operacją, co sugeruje korzyść w zakresie przeżycia. Jednakże, te krzywe przeżycia są szacowane na podstawie małych próbek. Aby porównać przeżycie między grupami, możemy użyć testu log rank. Hipotezą zerową jest, że nie ma różnicy w przeżyciu między dwiema grupami lub że nie ma różnicy między populacjami w prawdopodobieństwie śmierci w jakimkolwiek punkcie. Test logarytmiczny jest testem nieparametrycznym i nie przyjmuje żadnych założeń dotyczących rozkładów przeżycia. W istocie, test log rank porównuje zaobserwowaną liczbę zdarzeń w każdej grupie z tym, czego można by się spodziewać, gdyby hipoteza zerowa była prawdziwa (tj, gdyby krzywe przeżycia były identyczne).

H0: Dwie krzywe przeżycia są identyczne (lub S1t = S2t) versus H1: Dwie krzywe przeżycia nie są identyczne (lub S1t ≠ S2t, w dowolnym czasie t) (α=0.05).

Statystyka log rank jest w przybliżeniu dystrybuowana jako statystyka testu chi kwadrat. Istnieje kilka postaci tej statystyki testowej, a różnią się one sposobem obliczania. My używamy następującej:

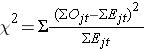
gdzie ΣOjt reprezentuje sumę zaobserwowanej liczby zdarzeń w j-tej grupie w czasie (np., j=1,2) i ΣEjt reprezentuje sumę oczekiwanej liczby zdarzeń w j-tej grupie w czasie.

Sumy zaobserwowanych i oczekiwanych liczb zdarzeń są obliczane dla każdego czasu zdarzenia i sumowane dla każdej grupy porównawczej. Statystyka logarytmiczna rang ma stopnie swobody równe k-1, gdzie k oznacza liczbę grup porównawczych. W tym przykładzie k=2, więc statystyka testowa ma 1 stopień swobody.

Do obliczenia statystyki testowej potrzebujemy obserwowanej i oczekiwanej liczby zdarzeń w każdym czasie zdarzenia. Obserwowana liczba zdarzeń pochodzi z próby, a oczekiwana liczba zdarzeń jest obliczana przy założeniu, że hipoteza zerowa jest prawdziwa (tzn. że krzywe przeżycia są identyczne).

Aby wygenerować oczekiwaną liczbę zdarzeń, organizujemy dane w tabelę życia z wierszami reprezentującymi każdy czas zdarzenia, niezależnie od grupy, w której zdarzenie wystąpiło. Śledzimy również przypisanie do grupy. Następnie szacujemy proporcję zdarzeń, które występują w każdym czasie (Ot/Nt), wykorzystując dane z obu grup łącznie przy założeniu braku różnicy w przeżywalności (tj. zakładając, że hipoteza zerowa jest prawdziwa). Mnożymy te szacunki przez liczbę uczestników zagrożonych w tym czasie w każdej z grup porównawczych (N1t i N2t odpowiednio dla grup 1 i 2).

Specyficznie, obliczamy dla każdego zdarzenia w czasie t, liczbę zagrożonych w każdej grupie, Njt (np. gdzie j oznacza grupę, j=1, 2) i liczbę zdarzeń (zgonów), Ojt , w każdej grupie. Poniższa tabela zawiera informacje potrzebne do przeprowadzenia testu log rank w celu porównania powyższych krzywych przeżycia. Grupa 1 reprezentuje grupę otrzymującą chemioterapię przed operacją, a grupa 2 grupę otrzymującą chemioterapię po operacji.

Data for Log Rank Test to Compare Survival Curves

.

Time, Months	Number at Risk in Group 1 N1t	Number at Risk in Group 2 N2t	Number of Events (Deaths) in Group 1 O1t	Number of Events (Deaths) in Group 1 O1t	Number Zdarzeń (Zgonów) w Grupie 2 O2t
8	10	10	1	0
12	8	10	1	0
14	7	10	1	0
21	5	10	1	0
26	4	8	1	0
27	3	8	1	0
28	2	8	0	1
33	1	7	0	1
41	0	5	0	1

Następnie sumujemy liczbę zagrożoną, Nt = N1t+N2t, w każdym czasie zdarzenia oraz liczbę zaobserwowanych zdarzeń (zgonów), Ot = O1t+O2t, w każdym czasie zdarzenia. Następnie obliczamy oczekiwaną liczbę zdarzeń w każdej grupie. Oczekiwana liczba zdarzeń jest obliczana dla każdego czasu zdarzenia w następujący sposób:

E1t = N1t*(Ot/Nt) dla grupy 1 i E2t = N2t*(Ot/Nt) dla grupy 2. Obliczenia są przedstawione w poniższej tabeli.

Przewidywana liczba zdarzeń w każdej grupie

Czas, Months	Number at Risk in Group 1 N1t	Number at Risk in Group 2 N2t	Total Number at Risk Nt .	Liczba zdarzeń w grupie 1 O1t	Liczba zdarzeń w grupie 2 O2t	Totalna liczba zdarzeń Ot	Oczekiwana liczba zdarzeń w Grupa 1 E1t = N1t*(Ot/Nt)	Oczekiwana liczba zdarzeń w Grupa 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000

Następnie sumujemy obserwowane liczby zdarzeń w każdej grupie (∑O1t i ΣO2t) oraz oczekiwane liczby zdarzeń w każdej grupie (ΣE1t i ΣE2t) w czasie. Są one przedstawione w dolnym wierszu kolejnej tabeli poniżej.

Total Observed and Expected Numbers of Observed in each Group

Time, Months	Number at Risk in Group 1 N1t	Number at Risk in Group 2 N2t	Total Number at Risk Nt .	Liczba zdarzeń w grupie 1 O1t	Liczba zdarzeń w grupie 2 O2t	Totalna liczba zdarzeń Ot	Oczekiwana liczba zdarzeń w Grupa 1 E1t = N1t*(Ot/Nt)	Oczekiwana liczba zdarzeń w Grupa 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000
				6	3		2.620	6.380

Możemy teraz obliczyć statystykę testową:

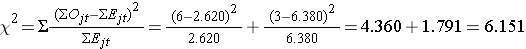
Statystyka testowa jest w przybliżeniu rozłożona jako chi kwadrat z 1 stopniem swobody. Zatem wartość krytyczną dla testu można znaleźć w tabeli Wartości krytyczne rozkładu Χ2.

Dla tego testu regułą decyzyjną jest odrzucenie H0, jeśli Χ2 > 3,84. Obserwujemy Χ2 = 6.151, co przekracza wartość krytyczną 3.84. W związku z tym odrzucamy H0. Mamy istotny dowód, α=0,05, wskazujący na to, że obie krzywe przeżycia są różne.

Przykład:

Badacz chce ocenić skuteczność krótkiej interwencji mającej na celu zapobieganie spożywaniu alkoholu w ciąży. Kobiety w ciąży, u których w przeszłości stwierdzono duże spożycie alkoholu, są rekrutowane do badania i randomizowane do otrzymania albo krótkiej interwencji skoncentrowanej na abstynencji od alkoholu, albo standardowej opieki prenatalnej. Interesującym wynikiem jest powrót do picia. Kobiety są rekrutowane do badania w około 18 tygodniu ciąży i obserwowane przez cały okres ciąży aż do porodu (około 39 tygodnia ciąży). Dane przedstawione poniżej wskazują, czy kobiety wracają do picia, a jeśli tak, to kiedy po raz pierwszy piją, mierzone w liczbie tygodni od randomizacji. W przypadku kobiet, u których nie nastąpił nawrót picia, odnotowujemy liczbę tygodni od randomizacji, w ciągu których nie piły alkoholu.

.

.

Standardowa opieka prenatalna			Krótka interwencja
Powrót	Bez nawrotu		Powrót	Bez nawrotu	Bez nawrotu
19	20		16	21
6	19		21	15
5	17		7	18
4	14			18
				5

Przedmiotem zainteresowania jest to, czy istnieje różnica w czasie do nawrotu choroby między kobietami przydzielonymi do standardowej opieki prenatalnej w porównaniu z kobietami przydzielonymi do krótkiej interwencji.

• Krok 1.

Postawić hipotezy i określić poziom istotności.

H0: Czas wolny od nawrotu jest identyczny między grupami vs

H1: Czas wolny od nawrotu nie jest identyczny między grupami (α=0,05)

• Krok 2.

Wybrać odpowiednią statystykę testu.

Statystyka testowa dla testu logarytmicznego rang wynosi

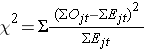
• Krok 3.

Ustalenie reguły decyzyjnej.

Statystyka testowa podąża za rozkładem chi kwadrat, a więc znajdujemy wartość krytyczną w tabeli wartości krytycznych dla rozkładu Χ2) dla df=k-1=2-1=1 i α=0,05. Wartość krytyczna wynosi 3,84 i regułą decyzyjną jest odrzucenie H0, jeśli Χ2 > 3,84.

• Krok 4.

Oblicz statystykę testu.

Aby obliczyć statystykę testu, porządkujemy dane według czasu zdarzenia (nawrotu) i określamy liczby kobiet zagrożonych w każdej grupie leczenia oraz liczbę, która nawraca w każdym zaobserwowanym czasie nawrotu. W poniższej tabeli grupa 1 reprezentuje kobiety, które otrzymują standardową opiekę prenatalną, a grupa 2 reprezentuje kobiety, które otrzymują krótką interwencję.

.

Czas, Tygodnie	Liczba osób zagrożonych – Grupa 1 N1t	Liczba osób zagrożonych – Grupa 2 N2t	Liczba nawrotów – Grupa 1 Grupa 2 O2t
4	8	8	8	1	0
5	7	8	1	0
6	6	7	1	0
7	5	7	0	1
16	4	5	0	1
19	3	2	1	0
21	0	2	0	1

Następnie sumujemy liczbę zagrożonych, 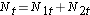, w każdym czasie trwania zdarzenia, liczbę zaobserwowanych zdarzeń (nawrotów), 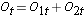, w każdym czasie trwania zdarzenia i określamy oczekiwaną liczbę nawrotów w każdej grupie w każdym czasie trwania zdarzenia, używając 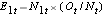i .

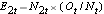Czas, Weeks	Number at Risk Group 1 N1t	Number at Risk Group 2 N2t	Total Number at Risk Nt	Total Number at Risk Nt	. Liczba nawrotów Grupa 1 O1t	Liczba nawrotów Grupa 2 O2t	Ogólna liczba nawrotów Ot	Przewidywana liczba nawrotów w grupie 1	Przewidywana liczba nawrotów w grupie 2
4	8	8	16	1	0	1	0.500	0.500
5	7	8	15	1	0	1	0.467	0.533
6	6	7	13	1	0	1	0.462	0.538
7	5	7	12	0	1	1	0.417	0.583
16	4	5	9	0	1	1	0.444	0.556
19	3	2	5	1	0	1	0.600	0.400
21	0	2	2	0	1	1	0.000	1.000
				4	3		2.890	4.110

Obliczymy teraz statystykę testową:

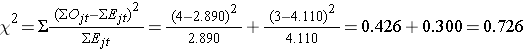
• Krok 5.

Wniosek. Nie odrzucać H0, ponieważ 0,726 < 3,84. Nie mamy statystycznie istotnych dowodów przy α=0,05, aby wykazać, że czas do nawrotu jest różny między grupami.

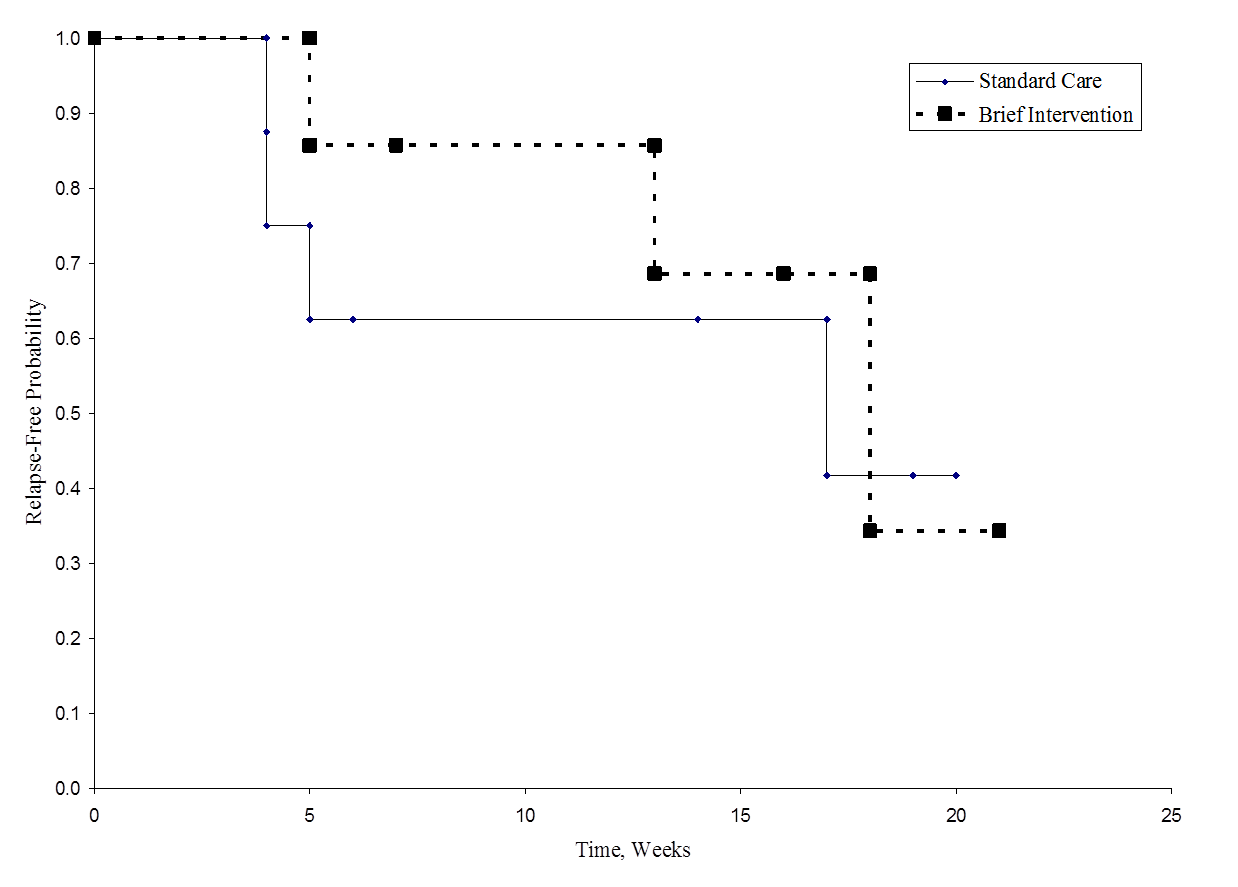
Poniższy rysunek przedstawia przeżycie (czas wolny od nawrotu) w każdej grupie. Zauważ, że krzywe przeżycia nie wykazują dużej separacji, co jest zgodne z nieistotnymi wynikami testu hipotezy.

Czas wolny od nawrotu w każdej grupie

Jak zauważono, istnieje kilka odmian statystyki log rank. Niektóre pakiety do obliczeń statystycznych używają następującej statystyki testu log rank do porównania dwóch niezależnych grup:

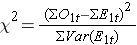
gdzie ΣO1t jest sumą zaobserwowanej liczby zdarzeń w grupie 1, a ΣE1t jest sumą oczekiwanej liczby zdarzeń w grupie 1 wziętej przez wszystkie czasy zdarzeń. Mianownik jest sumą wariancji oczekiwanych liczb zdarzeń w każdym czasie zdarzenia, która jest obliczana w następujący sposób:

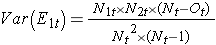
Istnieją inne wersje statystyki log rank, jak również inne testy do porównania funkcji przeżycia pomiędzy niezależnymi grupami.7-9 Na przykład popularnym testem jest zmodyfikowany test Wilcoxona, który jest wrażliwy na większe różnice w zagrożeniach we wcześniejszym okresie obserwacji w porównaniu z późniejszym.10

powrót do góry | poprzednia strona | następna strona

.