Elektromagnetyczny metamateriał oddziałuje na fale elektromagnetyczne, które padają na lub oddziałują z jego cechami strukturalnymi, które są mniejsze niż długość fali. Aby zachowywać się jak jednorodny materiał dokładnie opisany przez efektywny współczynnik załamania światła, jego cechy muszą być znacznie mniejsze niż długość fali.

Dla promieniowania mikrofalowego, cechy są rzędu milimetrów. Metamateriały o częstotliwości mikrofalowej są zwykle konstruowane jako tablice elementów przewodzących prąd elektryczny (takich jak pętle z drutu), które mają odpowiednią charakterystykę indukcyjną i pojemnościową. Wiele metamateriałów mikrofalowych wykorzystuje rezonatory pierścieniowe dzielone.

Metamateriały fotoniczne mają strukturę w skali nanometrów i manipulują światłem przy częstotliwościach optycznych. Kryształy fotoniczne i powierzchnie selektywne pod względem częstotliwości, takie jak siatki dyfrakcyjne, lustra dielektryczne i powłoki optyczne wykazują podobieństwa do metamateriałów o strukturze podfalowej. Są one jednak zwykle uważane za odmienne od metamateriałów, ponieważ ich funkcja wynika z dyfrakcji lub interferencji i dlatego nie mogą być przybliżone jako jednorodny materiał. Jednakże struktury materiałowe takie jak kryształy fotoniczne są efektywne w spektrum światła widzialnego. Środek spektrum widzialnego ma długość fali około 560 nm (dla światła słonecznego). Struktury kryształów fotonicznych są zazwyczaj o połowę mniejsze lub mniejsze, czyli <280 nm.

Metamateriały plazmoniczne wykorzystują plazmony powierzchniowe, czyli pakiety ładunków elektrycznych, które kolektywnie oscylują na powierzchniach metali przy częstotliwościach optycznych.

Powierzchnie selektywne pod względem częstotliwości (FSS) mogą wykazywać charakterystykę podfalową i są znane pod różnymi nazwami: sztuczne przewodniki magnetyczne (AMC) lub powierzchnie o wysokiej impedancji (HIS). FSS wykazują charakterystyki indukcyjne i pojemnościowe, które są bezpośrednio związane z ich strukturą podpoziomową.

Metamateriały elektromagnetyczne można podzielić na różne klasy, jak poniżej:

Ujemny współczynnik załamaniaEdit

Porównanie załamania w metamateriale lewoskrętnym do załamania w normalnym materiale

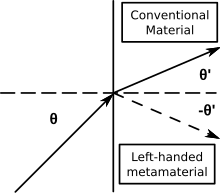
Metamateriały o ujemnym indeksie (NIM) charakteryzują się ujemnym indeksem załamania. Inne określenia dla NIM obejmują „media lewoskrętne”, „media o ujemnym współczynniku załamania” i „media o fali wstecznej”. NIM, w których ujemny współczynnik załamania powstaje z jednoczesnej ujemnej przenikalności i ujemnej przepuszczalności, są również znane jako metamateriały podwójnie ujemne lub materiały podwójnie ujemne (DNG).

Zakładając materiał dobrze przybliżony przez rzeczywistą przenikalność i przepuszczalność, zależność między przenikalnością ϵ r {{displaystyle \epsilon _{r}}

, przenikalnością μ r {{displaystyle \mu _{r}}

, a współczynnik załamania światła n jest dany wzorem n = ± ϵ r μ r { {displaystyle \scriptstyle n= \sqrt {\epsilon _{mathrm {{r}} } }mu _{mathrm {r} }}}}

. Wszystkie znane niemetamaterialne materiały przezroczyste (szkło, woda, …) posiadają dodatnią ϵ r {displaystyle \epsilon _{r}}.

i μ r {{displaystyle \mu _{r}}

. Zgodnie z konwencją, dodatni pierwiastek kwadratowy jest używany dla n. Jednakże, niektóre metamateriały mają ϵ r {{displaystyle \epsilon _{r}}

i μ r < 0 {displaystyle \mu _{r}<0}

. Ponieważ iloczyn ϵ r μ r {displaystyle \\\u0026apos; }

jest dodatni, to n jest rzeczywiste. W takich okolicznościach konieczne jest przyjęcie ujemnego pierwiastka kwadratowego dla n. Gdy oba ϵ r {displaystyle \epsilon _{r}}

jak i μ r {{displaystyle \mu _{r}}

są dodatnie (ujemne), fale rozchodzą się w kierunku do przodu (do tyłu). Fale elektromagnetyczne nie mogą rozchodzić się w materiałach o ϵ r {{displaystyle \u_epsilon _{r}}

i μ r {{displaystyle \mu _{r}}

o przeciwnym znaku, gdy współczynnik załamania staje się urojony. Takie materiały są nieprzezroczyste dla promieniowania elektromagnetycznego, a przykładem są materiały plazmoniczne, takie jak metale (złoto, srebro, …).

Powyższe rozważania są uproszczone dla rzeczywistych materiałów, które muszą mieć złożoną wartość ϵ r {{displaystyle \epsilon _{r}}

i μ r {{displaystyle \u _{r}}

. Rzeczywiste części obu ϵ r {displaystyle \epsilon _{r}}

oraz μ r {{displaystyle \mu _{r}}

nie muszą być ujemne, aby materiał pasywny wykazywał ujemne załamanie. Rzeczywiście, ujemny współczynnik załamania dla fal spolaryzowanych kołowo może również wynikać z chiralności. Metamateriały z ujemnym n mają wiele interesujących właściwości:

• Prawo Snella (n1sinθ1 = n2sinθ2) nadal opisuje załamanie, ale ponieważ n2 jest ujemne, promienie padające i załamane znajdują się po tej samej stronie normalnej powierzchni na granicy materiałów o dodatnim i ujemnym indeksie.
• Promieniowanie Czerenkowa wskazuje w drugą stronę.
• Uśredniony w czasie wektor Poyntinga jest antyrównoległy do prędkości fazowej. Jednak, aby fale (energia) mogły się rozchodzić, a -µ musi być sparowane z -ε, aby spełniona była zależność liczby falowej od parametrów materiału k c = ω μ ϵ {displaystyle kc= ω μ ϵ }}
  

  .

Ujemny współczynnik załamania wynika matematycznie z trójelementu wektorowego E, H i k.

Dla fal płaskich rozchodzących się w metamateriałach elektromagnetycznych pole elektryczne, pole magnetyczne i wektor falowy podążają za regułą lewej ręki, czyli odwrotnie niż w przypadku konwencjonalnych materiałów optycznych.

Do tej pory tylko metamateriały wykazują ujemny indeks załamania.

Single negativeEdit

Single negative (SNG) metamateriały mają albo ujemną względną przenikalność (εr) lub ujemną względną przenikalność (µr), ale nie obie. Działają one jako metamateriały, gdy są połączone z innym, komplementarnym SNG, wspólnie działając jako DNG.

Epsilon ujemne media (ENG) wykazują ujemną εr, podczas gdy µr jest dodatnia. Wiele plazm wykazuje tę właściwość. Na przykład, metale szlachetne takie jak złoto czy srebro są ENG w podczerwieni i widzialnym spektrum.

Mu-ujemne ośrodki (MNG) wykazują dodatnie εr i ujemne µr. Tę właściwość wykazują materiały żyrotropowe lub żyromagnetyczne. Materiał żyrotropowy to taki, który został zmieniony przez obecność quasistatycznego pola magnetycznego, umożliwiając efekt magnetooptyczny. Efekt magnetooptyczny to zjawisko polegające na rozchodzeniu się fali elektromagnetycznej w takim ośrodku. W takim materiale polaryzacje eliptyczne lewo- i prawoskrętna mogą rozchodzić się z różnymi prędkościami. Kiedy światło jest przepuszczane przez warstwę materiału magnetooptycznego, rezultat nazywany jest efektem Faradaya: płaszczyzna polaryzacji może zostać obrócona, tworząc rotator Faradaya. Rezultaty takiego odbicia znane są jako magnetooptyczny efekt Kerra (nie mylić z nieliniowym efektem Kerra). Dwa materiały żyrotropowe o odwróconych kierunkach rotacji dwóch głównych polaryzacji nazywane są izomerami optycznymi.

Połączenie płyty z materiału ENG i płyty z materiału MNG dało takie właściwości jak rezonanse, tunelowanie anomalne, przezroczystość i zerowe odbicie. Podobnie jak materiały o ujemnym indeksie, SNG są z natury dyspersyjne, więc ich εr, µr i współczynnik załamania n, są funkcją częstotliwości.

Metamateriały hiperboliczneEdit

Metamateriały hiperboliczne (HMM) zachowują się jak metal dla pewnej polaryzacji lub kierunku rozchodzenia się światła i zachowują się jak dielektryk dla innych ze względu na ujemne i dodatnie składowe tensora przenikalności, dając ekstremalną anizotropię. Relacja dyspersji materiału w przestrzeni wektorów falowych tworzy hiperboloidę i dlatego jest on nazywany metamateriałem hiperbolicznym. Skrajna anizotropia HMMs prowadzi do kierunkowej propagacji światła wewnątrz i na powierzchni. HMM wykazały różne potencjalne zastosowania, takie jak wykrywanie, obrazowanie, sterowanie sygnałami optycznymi, wzmocnione efekty rezonansu plazmonowego.

BandgapEdit

Elektromagnetyczne metamateriały bandgap (EBG lub EBM) kontrolują propagację światła. Osiąga się to za pomocą kryształów fotonicznych (PC) lub materiałów lewoskrętnych (LHM). PC mogą całkowicie uniemożliwić propagację światła. Obie klasy mogą pozwolić na propagację światła w określonych, zaprojektowanych kierunkach i obie mogą być zaprojektowane z przerwami pasmowymi dla pożądanych częstotliwości. Wielkość okresu EBGs jest znaczącym ułamkiem długości fali, tworząc konstruktywną i destrukcyjną interferencję.

PC są odróżniane od struktur o długości podwymiaru, takich jak przestrajalne metamateriały, ponieważ PC czerpie swoje właściwości z charakterystyki swojej przerwy pasmowej. PC mają rozmiary odpowiadające długości fali światła, w przeciwieństwie do innych metamateriałów, które eksponują strukturę podpoziomową. Ponadto, PC działają poprzez dyfrakcję światła. W przeciwieństwie do nich, metamateriał nie wykorzystuje dyfrakcji.

PC mają periodyczne wtrącenia, które hamują propagację fali z powodu destrukcyjnej interferencji wtrąceń z rozpraszania. Własność fotonicznej przerwy pasmowej PC czyni je elektromagnetycznym analogiem elektronicznych kryształów półprzewodnikowych.

EBGs mają na celu tworzenie wysokiej jakości, niskostratnych, okresowych, dielektrycznych struktur. EBG wpływa na fotony w ten sam sposób, w jaki materiały półprzewodnikowe wpływają na elektrony. PC są doskonałym materiałem bandgap, ponieważ nie pozwalają na propagację światła. Każda jednostka zalecanej struktury okresowej działa jak jeden atom, choć o wiele większy rozmiar.

EBGs są zaprojektowane, aby zapobiec propagacji przydzielonego pasma częstotliwości, dla pewnych kątów przybycia i polaryzacji. Różne geometrie i struktury zostały zaproponowane do produkcji EBG’s specjalne właściwości. W praktyce niemożliwe jest zbudowanie bezbłędnego urządzenia EBG.

EBGs zostały wyprodukowane dla częstotliwości w zakresie od kilku gigaherców (GHz) do kilku teraherców (THz), radio, mikrofale i mid-infrared regionach częstotliwości. Rozwój aplikacji EBG obejmuje linię transmisyjną, pale drewniane wykonane z kwadratowych prętów dielektrycznych i kilka różnych typów anten o niskim zysku.

Podwójnie dodatnie mediumEdit

Podwójnie dodatnie media (DPS) występują w przyrodzie, takie jak naturalnie występujące dielektryki. Przenikalność i przenikalność magnetyczna są zarówno dodatnie, a propagacja fali jest w kierunku do przodu. Wyprodukowano sztuczne materiały, które łączą właściwości DPS, ENG i MNG.

Bi-izotropowe i bianizotropoweEdit

Kategoryzacja metamateriałów na podwójnie lub pojedynczo ujemne, lub podwójnie dodatnie, zwykle zakłada, że metamateriał ma niezależne odpowiedzi elektryczne i magnetyczne opisane przez ε i µ. Jednakże, w wielu przypadkach, pole elektryczne powoduje polaryzację magnetyczną, podczas gdy pole magnetyczne indukuje polaryzację elektryczną, znaną jako sprzężenie magnetoelektryczne. Takie ośrodki są określane jako dwuizotropowe. Media, które wykazują sprzężenie magnetoelektryczne i które są anizotropowe (co ma miejsce w przypadku wielu struktur metamateriałowych), są określane jako bi-anizotropowe.

Cztery parametry materiałowe są nieodłączne od sprzężenia magnetoelektrycznego mediów bi-izotropowych. Są to natężenia pola elektrycznego (E) i magnetycznego (H) oraz gęstości strumienia elektrycznego (D) i magnetycznego (B). Parametry te to ε, µ, κ i χ czyli odpowiednio: przenikalność, przepuszczalność, siła chiralności i parametr Tellegena. W tego typu ośrodkach parametry materiałowe nie zmieniają się przy zmianach wzdłuż obróconego układu współrzędnych pomiarowych. W tym sensie są one niezmienne lub skalarne.

Wewnętrzne parametry magnetoelektryczne, κ i χ, wpływają na fazę fali. Efektem parametru chiralności jest podział współczynnika załamania. W ośrodkach izotropowych powoduje to propagację fali tylko wtedy, gdy ε i µ mają ten sam znak. W ośrodkach dwuizotropowych, gdzie χ przyjmuje się za zero, a κ za wartość niezerową, pojawiają się inne rezultaty. Może wystąpić albo fala wsteczna albo fala do przodu. Alternatywnie, mogą wystąpić dwie fale do przodu lub dwie fale do tyłu, w zależności od siły parametru chiralności.

W ogólnym przypadku, zależności konstytutywne dla materiałów dwuizotropowych mają postać D = ϵ E + ξ H , {displaystyle \mathbf {D} = \epsilon \mathbf {E} +xi \mathbf {H} ,}

B = ζ E + μ H , {displaystyle \mathbf {B} = \zeta \mathbf {E} +mu \mathbf {H} ,}

gdzie ϵ {displaystyle \epsilon }

oraz μ { {displaystyle \mu }

są odpowiednio tensorami przenikalności i pojemności, natomiast ξ {displaystyle \xi }

i ζ {displaystyle \zeta }

są dwoma tensorami magnetoelektrycznymi. Jeżeli ośrodek jest wzajemnie odwrotny, to przenikalność i przenikalność są tensorami symetrycznymi, a ξ = – ζ T = – i κ T {displaystyle \xi =- \zeta ^{T}=-i \kappa ^{T}}

, gdzie κ {{displaystyle \kappa }

jest tensorem chiralnym opisującym chiralną odpowiedź elektromagnetyczną i wzajemną odpowiedź magnetoelektryczną. Tensor chiralny może być wyrażony jako κ = 1 3 tr ( κ ) I + N + J { {tfrac {1}{3}}operatorname {tr} (\kappa )I+N+J}

, gdzie tr ( κ ) {{displaystyle \operatorname {tr} (\kappa )}

jest śladem κ {{displaystyle \kappa }

, I jest macierzą tożsamości, N jest symetrycznym tensorem bezśladowym, a J jest tensorem antysymetrycznym. Taka dekompozycja pozwala nam na klasyfikację odwrotnej odpowiedzi bianizotropowej i możemy wyróżnić następujące trzy główne klasy: (i) nośniki chiralne ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {displaystyle \operatorname {tr} (\kappa )\neq 0,N \neq 0,J=0}

), (ii) nośniki pseudochiralne ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {displaystyle \operatorname {tr} (\kappa )=0,N \neq 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {displaystyle \operatorname {tr} (\kappa )=0,N=0,J 0}

).

ChiralEdit

Handedness of metamaterials is a potential source of confusion as the metamaterial literature includes two conflicting uses of the terms left- and right-handed. Pierwszy z nich odnosi się do jednej z dwóch kołowo spolaryzowanych fal, które są trybami propagacji w ośrodkach chiralnych. Drugi odnosi się do trypletu pola elektrycznego, pola magnetycznego i wektora Poyntinga, które powstają w ośrodkach o ujemnym współczynniku załamania, które w większości przypadków nie są chiralne.

Generalnie chiralna i/lub bianisotropowa odpowiedź elektromagnetyczna jest konsekwencją geometrycznej chiralności 3D: metamateriały 3D-chiralne są tworzone przez osadzanie struktur 3D-chiralnych w ośrodku głównym i wykazują efekty polaryzacyjne związane z chiralnością, takie jak aktywność optyczna i dichroizm kołowy. Istnieje również pojęcie chiralności 2D i mówi się, że obiekt planarny jest chiralny, jeśli nie może być nałożony na swoje lustrzane odbicie, chyba że zostanie podniesiony z płaszczyzny. 2D-chiralne metamateriały, które są anizotropowe i stratne, wykazują kierunkowo asymetryczną transmisję (odbicie, absorpcję) fal spolaryzowanych kołowo z powodu dichroizmu konwersji kołowej. Z drugiej strony, bianisotropowa odpowiedź może powstać z geometrycznych struktur achiralnych nie posiadających ani 2D ani 3D wewnętrznej chiralności. Plum i współpracownicy badali sprzężenie magneto-elektryczne spowodowane zewnętrzną chiralnością, gdzie ułożenie struktury (achiralnej) wraz z wektorem fali promieniowania jest inne niż jej lustrzane odbicie, i zaobserwowali dużą, przestrajalną liniową aktywność optyczną, nieliniową aktywność optyczną, spekularną aktywność optyczną i kołowy dichroizm konwersyjny. Rizza i wsp. zaproponowali metamateriały chiralne 1D, w których efektywny tensor chiralności nie jest zanikający, jeśli układ jest geometrycznie jednowymiarowo chiralny (nie można na niego nałożyć lustrzanego odbicia całej struktury stosując translacje bez rotacji).

Metamateriały chiralne 3D są zbudowane z materiałów chiralnych lub rezonatorów, w których efektywny parametr chiralności κ { {przyp. tłum.}

kappa

jest niezerowy. Właściwości propagacji fal w takich chiralnych metamateriałach pokazują, że ujemne załamanie może być realizowane w metamateriałach o silnej chiralności i dodatniej ϵ r {displaystyle \epsilon _{r}}

oraz μ r {{displaystyle \u _{r}}

współczynnik załamania _{r}}

. Wynika to z faktu, że współczynnik załamania światła n {displaystyle n}

ma różne wartości dla fal lewostronnie i prawostronnie spolaryzowanych kołowo, dany wzorem

n = ± ϵ r μ r ± κ {displaystyle n= {sqrt {{epsilon _{r}}mu _{r}}} \ppa }

Widać, że ujemny indeks wystąpi dla jednej polaryzacji, jeśli κ {displaystyle \kappa }

kappa

> ϵ r μ r {displaystyle {{sqrt {{epsilon _{r}}}mu _{r}}}}

. W tym przypadku nie jest konieczne, aby jedno lub oba ϵ r {displaystyle \epsilon _{r}}

}

być ujemne dla propagacji fali wstecznej. Ujemny współczynnik załamania spowodowany chiralnością został po raz pierwszy zaobserwowany jednocześnie i niezależnie przez Plum et al. oraz Zhang et al. w 2009 roku.

FSS basedEdit

Main article: Tunable metamaterials § Frequency selective surface based metamaterials

Frequency selective surface-based metamaterials blokują sygnały w jednym paśmie fal i przepuszczają te na innym paśmie fal. Stały się one alternatywą dla metamateriałów o stałej częstotliwości. Pozwalają na opcjonalne zmiany częstotliwości w pojedynczym medium, zamiast restrykcyjnych ograniczeń stałej odpowiedzi częstotliwościowej.

.