Hello Folks! W tym artykule, będę opisywał algorytm używany w Natural Language Processing: Latent Semantic Analysis ( LSA ).
Główne zastosowania tej wspomnianej metody są szeroko zakrojone w lingwistyce: Porównywanie dokumentów w przestrzeniach niskowymiarowych (Document Similarity), Znajdowanie powtarzających się tematów w dokumentach (Topic Modeling), Znajdowanie relacji między terminami (Text Synoymity).

Wprowadzenie
Model Latent Semantic Analysis jest teorią dotyczącą tego, w jaki sposób reprezentacje znaczenia Aby wyodrębnić i zrozumieć wzorce z dokumentów, LSA z natury opiera się na pewnych założeniach: Latentna Analiza Semantyczna (LSA) obejmuje pewne operacje matematyczne w celu uzyskania wglądu w dokument. Algorytm ten stanowi podstawę Modelowania Tematycznego. Podstawową ideą jest wzięcie macierzy tego, co mamy – dokumentów i terminów – i rozłożenie jej na oddzielną macierz dokument-temat i macierz temat-term. Pierwszym krokiem jest wygenerowanie naszej macierzy dokument-term przy użyciu Tf-IDF Vectorizer. Można ją również skonstruować przy użyciu Bag-of-Words Model, ale wyniki są skąpe i nie wnoszą żadnego znaczenia do sprawy. Intuicyjnie, termin ma dużą wagę, gdy występuje często w dokumencie, ale rzadko w korpusie. Ponieważ Topic Modeling jest z natury algorytmem nienadzorowanym, musimy wcześniej określić ukryte tematy. Jest to analogiczne do klasteryzacji K-Means Clustering, w której określamy wcześniej liczbę klastrów. W tym przypadku wykonujemy aproksymację Low-Rank Approximation wykorzystując technikę redukcji wymiarowości za pomocą Truncated Singular Value Decomposition (SVD). Truncated SVD redukuje wymiarowość wybierając tylko t największych wartości singularnych i zachowując tylko pierwsze t kolumn U i V. W tym przypadku, t jest hiperparametrem, który możemy wybrać i dostosować, aby odzwierciedlić liczbę tematów, które chcemy znaleźć. Uwaga: Truncated SVD dokonuje redukcji wymiarowości, a nie SVD! Mając te wektory dokumentów i wektory terminów, możemy teraz łatwo zastosować miary takie jak podobieństwo cosinusowe do oceny: Algorytm ten jest używany głównie w różnych zadaniach opartych na NLP i jest podstawą dla bardziej solidnych metod, takich jak Probabilistic LSA i Latent Dirichlet Allocation (LDA). Kushal Vala, Junior Data Scientist w Datametica Solutions Pvt Ltd .
mogą być uczone na podstawie napotkania dużych próbek języka bez wyraźnych wskazówek co do jego struktury.
1) Znaczenie zdań lub dokumentów jest sumą znaczeń wszystkich występujących w nich słów. Ogólnie rzecz biorąc, znaczenie danego słowa jest średnią ze wszystkich dokumentów, w których występuje.
2) LSA zakłada, że związki semantyczne między słowami nie są obecne jawnie, ale tylko utajone w dużej próbce języka.Perspektywa matematyczna
Dając m dokumentów i n słów w naszym słowniku, możemy skonstruować macierz
m × n A, w której każdy wiersz reprezentuje dokument, a każda kolumna słowo.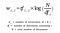
Utworzymy macierz dokumentów-terminów, A, używając tej metody transformacji (tf-IDF) do wektoryzacji naszego korpusu. (W sposób, który nasz dalszy model może przetworzyć lub ocenić, ponieważ nie pracujemy jeszcze na ciągach znaków!)
Jest jednak pewna subtelna wada, nie możemy niczego wywnioskować obserwując A, ponieważ jest to hałaśliwa i rzadka macierz. (Czasami zbyt duża, aby ją nawet obliczyć dla dalszych procesów).
Singular value decomposition jest techniką w algebrze liniowej, która faktoryzuje dowolną macierz M do iloczynu 3 oddzielnych macierzy: M=U*S*V, gdzie S jest diagonalną macierzą wartości singularnych M.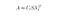

Uwagi końcowe