Teoria Galois para nãomatemáticos

Como um adolescente inventou um novo ramo da matemática para resolver uma questão aberta há muito tempo sobre equações

Você deve saber que para resolver uma equação de grau 2, ax²+bx+c = 0, usamos a fórmula quadrática.

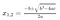
Existem fórmulas semelhantes para equações de grau 3 e 4, mas misteriosamente faltam para 5 ou superior. Mais especificamente, parece que não podemos construir as soluções para o quíntico (equação de grau 5) ou superior usando apenas adição, subtração, multiplicação, divisão e radicais (raízes quadradas, raízes cúbicas, etc). Por que isso, o que há de tão especial no número 5? Estas foram perguntas que assombraram o jovem francês Evariste Galois no início do século XIX, e na noite antes de ser fatalmente ferido num duelo, ele escreveu uma teoria de um novo objeto matemático chamado “grupo” que resolve a questão de uma forma surpreendentemente elegante.

Galois sendo baleado num duelo. Imagem de Wikimedia.

Foi assim que ele fez.

O conjunto de raízes de diferentes equações são de complexidade diferente. Alguns conjuntos são tão complexos que não podem ser expressos usando apenas objetos simples, como os radicais. Mas como podemos medir a complexidade das raízes se nem sequer as podemos calcular, e que medida de complexidade devemos usar?

Raízes germinantes e simetria

A resposta está na simetria das raízes.

Simetria das raízes que se pode perguntar, o que é que isso tem a ver com alguma coisa? O que é que isso quer dizer?

Vamos traçar as raízes de duas equações e ver se conseguimos dar-lhe sentido:

Diz-se que a da esquerda é menos simétrica que a da direita. Isto pode surpreendê-lo, porque no sentido coloquial da palavra, simétrico é normalmente usado se se pode reflectir ou rodar o objecto sem alterar a sua aparência. Nesse sentido, a imagem da esquerda parece mais simétrica.

Por exemplo: A estrela é mais simétrica que o coração, porque além de refleti-la, também se pode girá-la.

Mas, no nosso caso, vamos ter uma visão mais geral das simetrias. Não nos restringimos apenas a reflexos e rotações, qualquer função que transforme o objecto sem alterar a sua aparência é um jogo justo. No caso das raízes, isso significa que qualquer função que interfira (permuta) as raízes de qualquer forma é válida. Mais funções significam mais simétricas.

Acontece que no caso certo, existem funções para permutar todas as raízes em qualquer ordem concebível, tantas quantas 5!=120, por isso é altamente simétrica. Mas no caso da esquerda, se trocarmos r₂↔r₄ usando a transformação i↔-i, necessariamente também trocamos r₁↔r₅. Isto nos restringe, e assim todas as permutações concebíveis não são possíveis. É menos simétrico.

As funções que permutam as raízes são chamadas de “Automorfismos”, e se agruparmos esses automorfismos, obtemos o que é chamado de “Grupo” (mais tarde voltarei a melhores definições de automorfismos e grupos).

O que significa que o grupo que representa as simetrias das raízes é maior e mais complexo no caso certo. Na verdade, o grupo no caso certo é tão complexo que as raízes não podem ser descritas usando radicais.

Como sabemos o quão complexo é um grupo? Para entender isso precisamos de um pouco mais de teoria.

O tamanho do quintico

Primeiro, vamos dar uma olhada no tamanho de um grupo. Como sei que existem alguns quinticos que têm um grupo 5! grande?

Um quintico geral normalmente se parece com isto:

x⁵+ax⁴+bx³+cx²+dx+e=0

Mas se tomarmos uma abordagem mais “centrada na raiz”, podemos dizer que se parece com isto:

(x-r₁)(x-r₂)(x-r₃)(x-r₄)(x-r₅)=
x⁵-(r₁+r₂+r₃+r₄+r₅)x⁴+
(r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₃r₅+r₄r₅)x³…- r₁r₂r₃r₄r₅=0

Isto é, a constante a,b,c,d,e na primeira equação é substituída por uma combinação simétrica das raízes:

r₁+r₂+r₃+r₄+r₅=a
r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅=b
(c e d omitidos para brevidade)
r₁r₂r₃r₄r₅ = e

Ver todos os termos em detalhe, descobre-se que a troca das raízes não afeta a equação (experimente para b acima, por exemplo). Isto é verdade para polinómios de qualquer grau. Como somos capazes de trocar todas as raízes, podemos concluir que o grupo de simetria para este quíntico geral é na verdade todas as permutações, também chamado S₅ (o grupo simétrico de ordem 5).

Campos e Autorfismos

Agora vamos expandir um pouco a nossa definição de autorfismos, pois eles são mais do que funções que permutam raízes. No processo precisamos de introduzir algo chamado “campos”. Porque quereríamos fazer isso, dizes tu? A razão é que, enquanto trabalhar com raízes e suas permutações é divertido, é um pouco mais fácil trabalhar com campos e seus automorfismos. São exactamente as mesmas funções, não te preocupes, apenas outra forma de olhar para eles.

Então, se a equação é, digamos x²-2=0, em vez de trabalhar com as raízes, r₁=√2, r₂=-√2 vamos introduzir o campo Q(√2). Estes são todos os números racionais Q com um √2 adicionado. √2 é chamado de “field extension” (extensão de campo). Parece assim: a+b√2 a,b∈Q. Para podermos descrever a raiz da equação, precisamos do campo Q(√2). Para cada extensão de campo (e também outros objetos matemáticos) temos um monte de funções, σₙ, que envia um número para outro número único no mesmo campo e segue a condição σ(a+b)=σ(a)+σ(b) e σ(ab)=σ(a)σ(b). σ é uma função da extensão e não toca o campo subjacente Q. Estas funções são chamadas de automorfismos. A propósito, elas também permutam as raízes. Isto é porque para a raiz r:

r⁵+ar⁴+br³+cr²+dr+e=0⟹
σ(r⁵+ar⁴+br³+cr²+dr+e)=σ(0)⟹
σ(r)⁵+aσ(r)⁴+bσ(r)³+cσ(r)²+dσ(r)+e=0 (uma vez que σ não toca em Q (onde a, b, c, d,e vive))

Isto significa que σ(r) também é uma solução para a equação. E desde:

σ(r₁)-σ(r₂)=σ(r₁)+σ(-1)σ(r₂)=σ(r₁-r₂)≠0

as raízes são distintas, portanto temos 5 delas, que devem ser as 5 originais. Assim σ deve permutar as raízes.

Obviamente, isto funciona para uma equação de qualquer grau.

Hence:

Temos a nossa equação.
Aquela equação tem um campo que pode conter uma extensão de alguns radicais
Aquela extensão de campo tem um grupo, que é um conjunto de todos os seus autorfismos.

Dois exemplos de Grau 3

Equação: x³-x²-2x+2=0

As raízes são (1,√2,-√2) (você mesmo pode verificar isso ligando-as), portanto o campo deve ser Q(√2)

Escrevendo todas as formas que podemos pensar para permutar as raízes (e significa permutação de identidade, não faz nada):

(e)
(√2↔-√2)
(1↔√2)
(1→-√2)
(√2→-√2 e 1→√2)
(√2↔-√2 e √2-√2)

Sejamos um teste: Que (√2↔-√2) seja σ₁:

σ₁(√2+-√2)=σ₁(0)=0=σ₁(√2)+σ₁(-√2)
σ₁((√2)(-√2))=σ₁(-2)=-2=σ₁(√2)σ₁(-√2)

Até agora tudo bem. Outro.

Let (1↔√2) seja σ₂:

σ₂(√2+-√2)=σ₂(0)=0 ≠ σ₂(√2)+σ₂(-√2)=1+-√2
σ₂((√2)(-√2))=2 ≠ σ₂(√2)σ₂(-(-√2)=1(-√2)

Aparentemente σ₂ não é um automorfismo, por isso vamos ter de o eliminar. O outro σ tem problemas semelhantes, os únicos que restam são o e e e σ₁. Isto é chamado de grupo cíclico C₂ já que só podemos permutar em um círculo (um círculo muito pequeno neste caso).

Exemplo 2

Equação: x³-2=0

As raízes são

so o campo deve ser

usando ζ para brevidade. Isto é o que parece:

Uma pessoa pode brincar um pouco com as permutações das raízes, e logo notará que neste caso são todos automorfismos. Assim existem 3! automorfismos, que são todas as permutações de raiz, portanto o grupo deve ser S₃.

Outra coisa divertida de se notar sobre a imagem acima é que ela parece um triângulo equilátero e que os automorfismos correspondem exatamente a girar e refletir o triângulo. Se os autómorfismos corresponderem às simetrias de um polígono regular desta forma, o grupo é chamado de “grupo Dihedral”. Neste caso, D₃. Normalmente o grupo de todas as permutações Sₙ não é o mesmo que o grupo diédrico Dₙ, mas no caso de n=3 é.

Grupos

Este parece ser um bom lugar para seguir para uma discussão um pouco mais longa sobre grupos. Assim, grupos começaram como coleções de permutações de raízes, mas também podem ser vistos como coleções de automorfismos, ou rotações e reflexos de objetos geométricos simétricos. Qualquer coleção de funções que altera um objeto de tal forma que ele pareça o mesmo pode ser considerado um grupo. Mas, podemos realmente olhar para as transformações em si sem nos preocuparmos com o objecto simétrico sobre o qual elas actuam. Da mesma forma que não nos preocupamos com pilhas de maçãs quando fazemos aritmética, simplesmente seguimos as regras, da mesma forma podemos definir algumas regras que as transformações de um grupo seguem, e usá-las.

As regras são algo como isto:

Se primeiro fizermos uma transformação, e depois outra, teremos uma terceira transformação que ainda está no grupo. Por exemplo, o grupo C₄ é o grupo de todas as rotações que se pode fazer em um quadrado. Se a está girando 90∘, b está girando 180∘ e c está girando 270∘ então a∗b=c. Onde ∗ significa, primeiro faça b e depois a, comumente chamado de multiplicação já que é (mais ou menos) semelhante à multiplicação de números. De acordo com a regra acima, c tem que estar no grupo. Isto é chamado de fechamento.

Tem que haver um elemento de identidade (e) que não faz nada.

Para cada elemento tem que haver um inverso desse elemento.

Agora, podemos investigar as características de diferentes grupos sem ter que nos preocupar com raízes ou polígonos.

Visualizar grupos

Duas divertidas maneiras de visualizar grupos são:

Tabelas Cayley

Acima é a tabela Caylay para um triângulo equilátero, o grupo D₃. São todos os elementos do grupo e que elementos obtemos quando os multiplicamos. Por exemplo, se primeiro fizermos uma rotação 120∘ (r) e depois a mesma rotação novamente obtemos uma rotação 240∘ rr=r² como pode ser visto na tabela. Se fizermos uma rotação 120∘ rotação-flip rf e um r acabamos com apenas um flip. Observe como os elementos f e r não se deslocam. Um grupo onde o elemento comuta é chamado de grupo abeliano.

Esta tabela em particular ainda é muito simétrica, mas não precisa de ser assim. Qualquer embaralhamento dos elementos que seguem as regras é válido.

Gráfico de Caylay

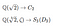
Parece que o segundo campo e grupo são mais complexos do que o primeiro campo e grupo. Podemos adivinhar isso contando apenas o número de termos no caso de campo ou o número de automatismos no caso de grupo. Mas a simples contagem não parece capturar realmente o que significa ser complexo. Veja, por exemplo, o grupo C₁₂. Muitos elementos, mas apenas gira as raízes, por isso não parece realmente tão complexo. Um campo correspondente é Q(e^π/6). Ele conterá e^π/6,e^2π/6… mas novamente, não muito complexo.

Pesar sobre o quão complexo um grupo é vai ser a chave para entender porque algumas raízes não podem ser descritas apenas por radicais, lembre-se.

Para obter uma melhor maneira de apreciar a complexidade, vamos introduzir o conceito de um “Subcampo” e um “Subgrupo”. Um subcampo é quando você remove alguns dos termos, mas você ainda tem um campo fechado. Da mesma forma, um subgrupo é quando você remove alguns dos automorfismos mas ainda tem um grupo fechado.

No primeiro caso Q(√2), a única coisa que se pode fazer é remover o √2 no campo e um dos dois automorfismos no grupo (não podemos remover (e) e ainda temos um grupo).

Como para o segundo caso Q(³√2, ζ), fica um pouco mais complicado. Pode-se destilar manualmente o subcampo/grupo removendo apenas os elementos um de cada vez e ver se o campo/grupo resultante está fechado. Depois de um tempo chegamos a isto:

Interessando, tanto o campo como o grupo têm quatro constituintes. Agora, seria um palpite razoável que os subgrupos contêm sempre exatamente os automorfismos dos subcampos. Mas eles não.

Camposixados

Não se preocupe, estamos quase lá, é apenas um pouco mais complicado. Para ver isso, vamos dar uma olhada no campo Q(⁴√2, i) e seus subcampos.

O campo Q(⁴√2, i) tem o grupo de permutação D₄ (igual a um quadrado). Vamos olhar para D₄ e seus subgrupos.

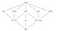
A malha do subgrupo está de cabeça para baixo nesta figura com D₄ na parte inferior, vou chegar a isso em breve, mas vamos primeiro olhar para os subcampos contra os subgrupos. Q(⁴√2, i) tem 5 subcampos grandes e 3 subcampos pequenos, mas D₄ tem apenas 3 subgrupos grandes e 5 subgrupos menores.

Parece que não há grupos grandes o suficiente para permutar os 5 campos grandes. Se você fosse brincar com os subgrupos e subcampos, você eventualmente chegaria à conclusão de que os subgrupos realmente não permutam os subcampos, mas sim tudo que não está nos subcampos, que eles “consertam” ou não tocam nos subcampos.

Então por exemplo (f) corrige Q(⁴√2) e (r², f) corrige Q(√2).

Porquê é desta forma e não o contrário, como adivinhámos inicialmente?

Não tenho uma forma intuitiva de explicar isto, a forma como o vejo é que o descobrimos empiricamente e agora podemos tentar prová-lo. A prova é mais ou menos assim:

Teorema fundamental da teoria de Galois, que é um esboço da prova

Queremos mostrar que se virarmos a malha do subgrupo de cabeça para baixo, obtemos uma correspondência um-a-um com a malha do subcampo onde os campos são os campos fixos dos grupos.

Primeiro, gostaria de salientar que é razoável (mais ou menos) que este seja o caso. No grupo inferior, temos todos os automorfismos, que naturalmente se movem em torno de tudo excepto Q (fixa Q), e no topo, temos apenas o e-automorfismo, que se move em torno de nada (fixa tudo).

Se começarmos no grupo inferior e removermos alguns dos automorfismos, os automorfismos removidos deixarão de se mover em torno de uma pequena parte do campo e assim irão fixar essa parte do campo. Como removemos mais automorfismos, uma parte maior e maior do campo não será mais afetada e assim teremos um campo fixo maior.

Para sermos um pouco mais rigorosos precisaremos ser capazes de comparar o tamanho do grupo e do campo. O tamanho do grupo é, naturalmente, o número de automorfismos nele existentes. O tamanho do campo é o número de termos. Estes dois são os mesmos, mas porquê?

Quotient

Agora, poderíamos olhar para a malha do subgrupo S₅ do quintic e ver que de facto parece bastante complexo. Mas para ligar isto aos radicais precisamos de uma maneira de analisar a complexidade entre os grupos e seus subgrupos. Ou seja: Quão mais complexo é D₄ do que C₄, por exemplo? Para isso, introduzimos o conceito de “Quociente”. Um quociente é basicamente uma divisão em grupos. Como isso funciona?

Na divisão comum, fazemos algo assim: Para dividir 15 maçãs em 5 pessoas, agrupamos as maçãs no conjunto de maçãs em 5 pilhas iguais e cada pilha corresponderá a uma pessoa no conjunto de pessoas. A resposta à pergunta 15/5 é 3, uma das pilhas, qualquer pilha fará, já que são iguais.

Uma coisa semelhante acontece quando dividimos grupos. Para dividir D₄ por C₄, agrupamos os 8 elementos de D₄ em 4 grupos iguais, um para cada elemento em C₄. Como fazemos para que os grupos sejam iguais? Não é como se os elementos fossem todos maçãs idênticas. Eles podem ser autómorfismos muito diferentes, por exemplo. Bem, nem sempre os quocientes são possíveis exactamente por essa razão. Mas às vezes um grupo pode ser dividido em “Cosets”. Digamos que dividimos D₄ em 4 partes iguais com 2 elementos em cada. Se tivermos sorte, podemos ter 4 pilhas de elementos onde a relação entre os dois elementos é a mesma em todas as pilhas. Para poder fazer isso o grupo original tem que exibir um alto nível de auto-similitude. Para ver isto, vejamos um gráfico de Cayley de D₄.

Como se pode ver, há de facto um elevado nível de auto-similitude aqui. Os cantos superior esquerdo, superior direito, inferior esquerdo e inferior direito têm todos o mesmo aspecto. Este é o nosso cosets.

Então D₄/C₄ é basicamente um destes cosets, que é C₂. Daí: D₄/C₄=C₂.

Agora, ao introduzirmos quocientes, temos um conceito de como construir grupos a partir do zero. Assim como o 21 consiste em 3 e 7, também os grupos consistem nos seus subgrupos. E assim como podemos obter os constituintes de um número dividindo, 21/7=3, assim podemos obter os constituintes de um grupo tomando o quociente. Desde D₄/C₄=C₂, isso significa que se tivermos um grupo C₄, temos de multiplicá-lo por C₂ para chegarmos a D₄. Como existe uma correspondência entre campos e grupos, isto terá um papel na forma como construímos os campos.