No tutorial de modelos lineares generalizados, aprendemos sobre várias GLM’s como regressão linear, regressão logística, etc. Neste tutorial da série R do TechVidvan, vamos analisar a regressão linear em R em detalhe. Vamos aprender o que é R regressão linear e como implementá-la em R. Vamos olhar para o método de estimativa mínima quadrada e também vamos aprender como verificar a precisão do modelo.

Então, sem mais delongas, vamos começar!

Regressão linear em R

Regressão linear em R é um método usado para prever o valor de uma variável usando o(s) valor(es) de uma ou mais variáveis preditor(es) de entrada. O objetivo da regressão linear é estabelecer uma relação linear entre a variável de output desejada e os preditores de entrada.

Para modelar uma variável contínua Y como uma função de uma ou mais variáveis preditoras de entrada Xi, para que a função possa ser usada para prever o valor de Y quando apenas os valores de Xi são conhecidos. A forma geral dessa relação linear é:

Y=?0+?1 X

Aqui, ?0 é a intercepção
e ?1 é a inclinação.

Tipos de Regressão Linear em R

Existem dois tipos de regressão linear R:

• Regressão Linear Simples
• Regressão Linear Múltipla

Vamos dar uma vista de olhos a estes um por um.

Regressão linear simples em R

Regressão linear simples destina-se a encontrar uma relação linear entre duas variáveis contínuas. É importante notar que a relação é de natureza estatística e não determinística.

Uma relação determinística é aquela em que o valor de uma variável pode ser encontrado com precisão usando o valor da outra variável. Um exemplo de uma relação determinística é aquela entre quilômetros e milhas. Usando o valor quilométrico, podemos encontrar com precisão a distância em milhas. Uma relação estatística não é precisa e tem sempre um erro de previsão. Por exemplo, com dados suficientes, podemos encontrar uma relação entre a altura e o peso de uma pessoa, mas sempre haverá uma margem de erro e casos excepcionais existirão.

A ideia por trás da regressão linear simples é encontrar uma linha que melhor se ajuste aos valores dados de ambas as variáveis. Esta linha pode então ajudar-nos a encontrar os valores da variável dependente quando eles estão ausentes.

Deixe-nos estudar isto com a ajuda de um exemplo. Temos um conjunto de dados que consiste nas alturas e pesos de 500 pessoas. Nosso objetivo aqui é construir um modelo de regressão linear que formule a relação entre altura e peso, de modo que quando damos altura(Y) como entrada para o modelo ele possa dar peso(X) em retorno a nós com margem ou erro mínimo.

Y=b0+b1X

Os valores de b0 e b1 devem ser escolhidos de modo que minimizem a margem de erro. O índice de erro pode ser usado para medir a precisão do modelo.

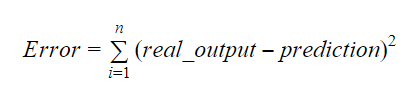
Podemos calcular a inclinação ou o coeficiente de erro como: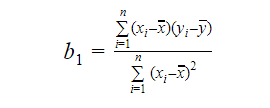

O valor de b1 dá-nos uma visão da natureza da relação entre as variáveis dependentes e as independentes.

• Se b1 > 0, então as variáveis têm uma relação positiva, ou seja aumento em x resultará num aumento em y.
• Se b1 < 0, então as variáveis têm uma relação negativa, ou seja, o aumento em x resultará numa diminuição em y.

O valor de b0 ou interceptar pode ser calculado da seguinte forma: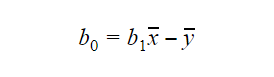
O valor de b0 também pode dar muita informação sobre o modelo e vice-versa.

Se o modelo não incluir x=0, então a previsão não tem sentido sem b1. Para que o modelo tenha apenas b0 e não b1 nele em qualquer ponto, o valor de x tem de ser 0 nesse ponto. Em casos como altura, x não pode ser 0 e a altura de uma pessoa não pode ser 0. Portanto, tal modelo não tem significado com apenas b0,

Se o termo b0 estiver faltando, então o modelo passará pela origem, o que significará que a previsão e o coeficiente de regressão (inclinação) serão tendenciosos.

Regressão linear múltipla em R

Regressão linear múltipla é uma extensão da regressão linear simples. Na regressão linear múltipla, o nosso objetivo é criar um modelo linear que possa prever o valor da variável alvo usando os valores de múltiplas variáveis preditoras. A forma geral de tal função é a seguinte:

Y=b0+b1X1+b2X2+…+bnXn

Avaliando a Precisão do Modelo

Existem vários métodos para avaliar a qualidade e precisão do modelo. Vamos dar uma olhada em alguns destes métodos um de cada vez.

R-Squared

A informação real nos dados é a variância transmitida nele. R-quadrado nos diz a proporção da variação na variável alvo (y) explicada pelo modelo. Podemos encontrar a medida de R-quadrado de um modelo usando a seguinte fórmula: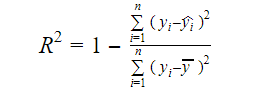

Where,

• yi é o valor ajustado de y para observação i
• y é a média de Y.

Um valor inferior de R-quadrado significa uma menor precisão do modelo. Entretanto, a medida de R-quadrado não é necessariamente um fator decisivo final.

Ajustado R-quadrado

A medida que o número de variáveis aumenta no modelo, o valor de R-quadrado também aumenta. Isto também causa erros na variação explicada pelas variáveis recém adicionadas. Portanto, ajustamos a fórmula do quadrado R para múltiplas variáveis.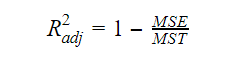
Aqui, MSE significa Erro Padrão Médio que é:

E MST significa Total Padrão Médio que é dado por: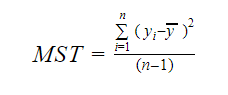

Onde, n é o número de observações e q é o número de coeficientes.

A relação entre R-quadrado e R-quadrado ajustado é: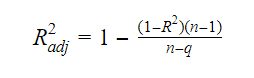

Erro Padrão e F-estatístico

O erro padrão e o F-estatístico são ambos medidas da qualidade do ajuste de um modelo. As fórmulas para o erro padrão e a estatística F são:

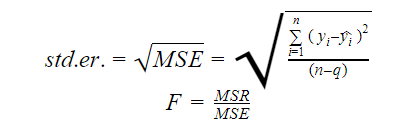
Onde MSR significa Regressão Quadrática Média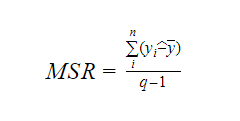

AIC e BIC

Critério de Informação de Akaike e Critério de Informação Bayesiana são medidas da qualidade do ajuste dos modelos estatísticos. Eles também podem ser usados como critérios para a seleção de um modelo.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Where,

• L é a função de probabilidade,
• k é o número de parâmetros do modelo,
• n é o tamanho da amostra.

funçãolm em R

A função lm() de R encaixa em modelos lineares. Ela pode realizar regressão, e análise de variância e covariância. A sintaxe da função lm é a seguinte:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Onde,

• fórmula é um objeto da classe “fórmula” e é uma representação simbólica do modelo a caber,
• dados é o quadro ou lista de dados que contém as variáveis na fórmula(dados é um argumento opcional. Se estiver faltando, a função pega as variáveis do ambiente),
• subconjunto é um vetor opcional contendo um subconjunto de observações que devem ser usadas no processo de ajuste,
• pesos é um vetor opcional que especifica os pesos a serem usados no processo de ajuste,
• na.ação é uma função que mostra o que deve acontecer quando NA são encontrados nos dados,
• método significa o método para o ajuste do modelo,
• modelo, x, y e qr são lógicas que controlam se os valores correspondentes devem ou não ser retornados com a saída. Estes valores são:
• modelo: a moldura do modelo
• x: a matriz do modelo
• y: a resposta
• qr: a decomposição qr
• singular.ok é uma lógica que controla se o singular encaixa ou não,
• offset é um preditor previamente conhecido que deve ser usado no modelo,
• . . são argumentos adicionais a serem passados para as funções de regressão de nível inferior,

Exemplo prático de regressão linear em R

É teoria suficiente por enquanto. Vamos dar uma olhada em como implementar tudo isso. Vamos ajustar um modelo linear usando a regressão linear em R com a ajuda da função lm(). Também vamos verificar a qualidade do ajuste do modelo depois. Vamos usar o conjunto de dados dos carros que é fornecido por padrão no pacote base R.

1. Vamos começar com uma análise gráfica do conjunto de dados para nos familiarizarmos mais com ele. Para fazer isso vamos desenhar um gráfico de dispersão e verificar o que ele nos diz sobre os dados.

Podemos usar a função scatter.smooth() para criar um gráfico de dispersão para o conjunto de dados.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Output

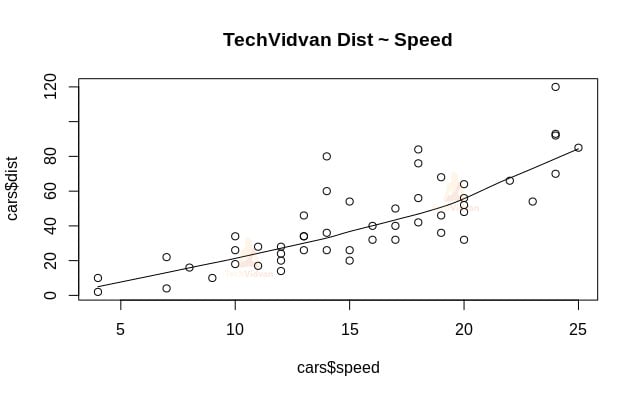
O gráfico de dispersão nos mostra uma correlação positiva entre distância e velocidade. Sugere uma relação linearmente crescente entre as duas variáveis. Isto torna os dados adequados para a regressão linear como uma relação linear é uma suposição básica para encaixar um modelo linear nos dados.

2. Agora que verificamos que a regressão linear é adequada para os dados, podemos usar a função lm() para encaixar um modelo linear a ele.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Output

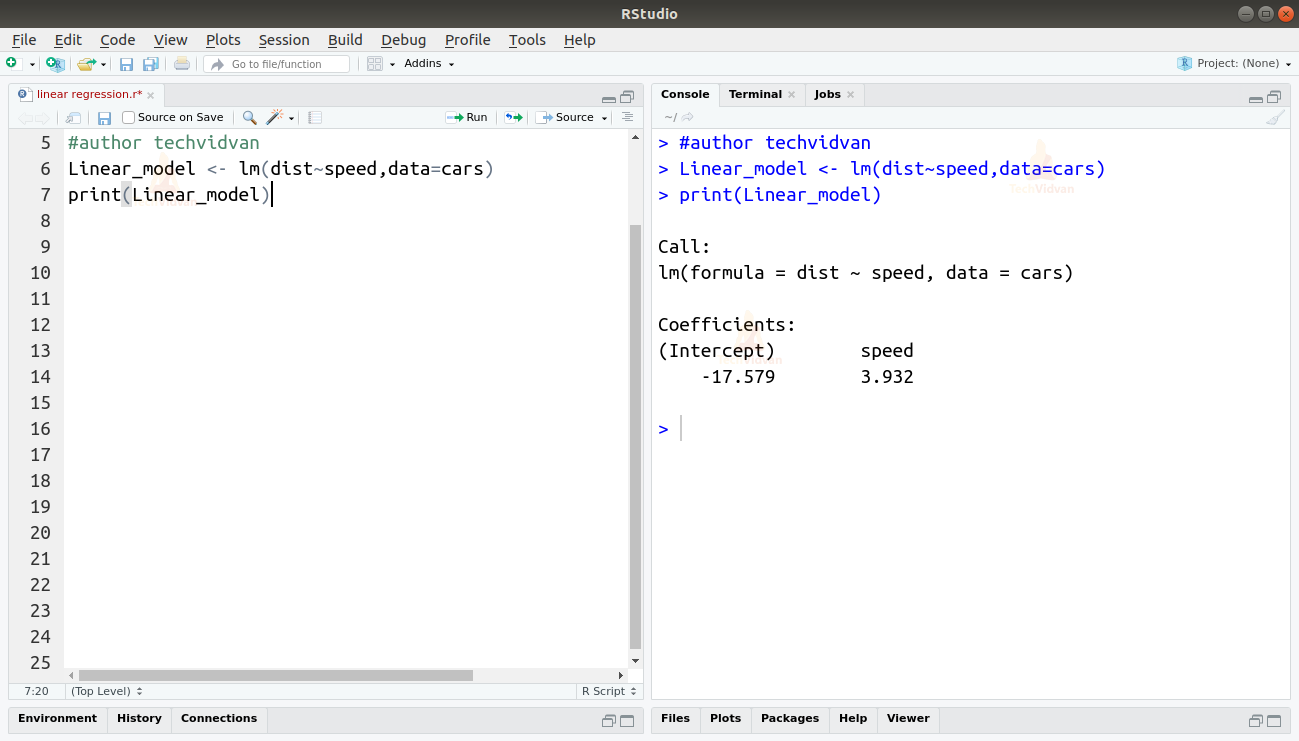
A saída da função lm() mostra-nos a intercepção e o coeficiente de velocidade. Assim definindo a relação linear entre distância e velocidade como:

Distance=Intercept+coefficient*speed

Distância=-17.579+3.932*speed

3. Agora que montamos um modelo, deixe-nos verificar a qualidade ou bondade do ajuste. Comecemos por verificar o resumo do modelo linear usando a função summary().

summary(Linear_model)

Output

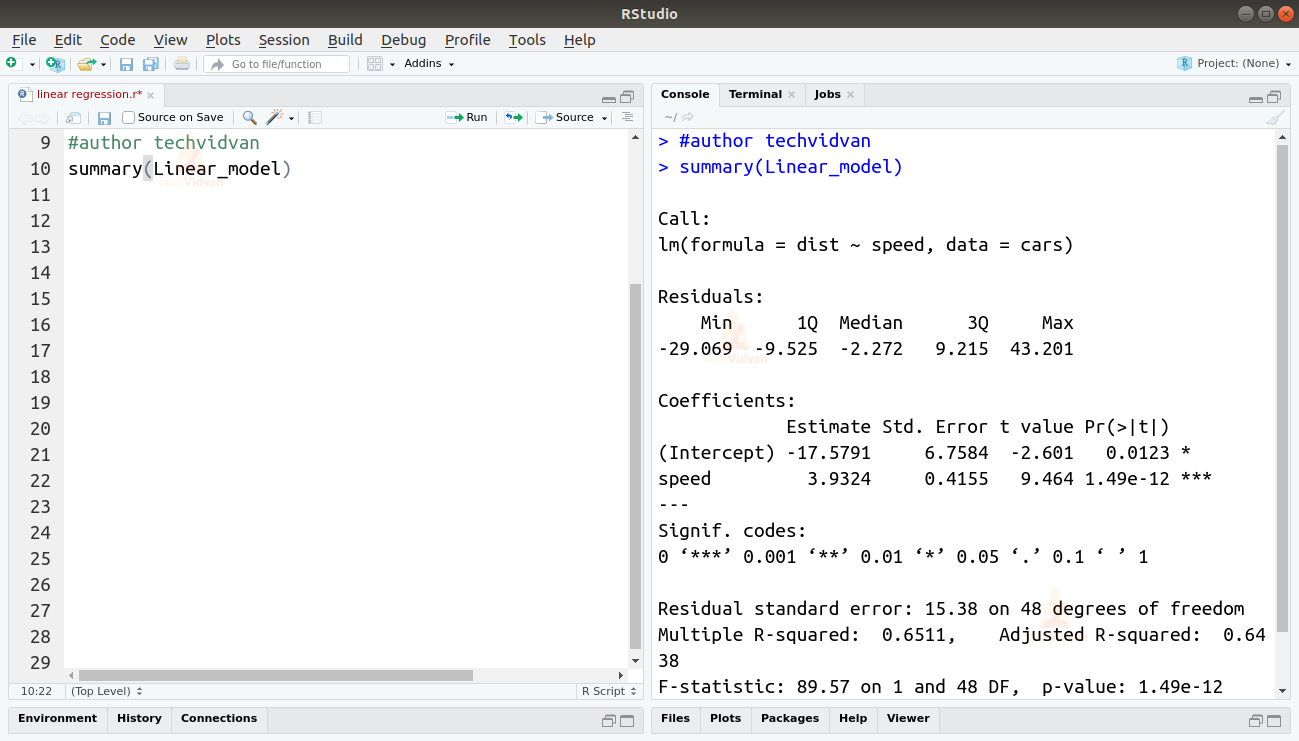
A função summary() dá-nos algumas medidas importantes para ajudar a diagnosticar o ajuste do modelo. O p-valor é uma medida importante da bondade do ajuste de um modelo. Diz-se que um modelo não é adequado se o valor p for mais do que um nível de significância estatística pré-determinado que é idealmente 0.05.

O sumário também nos fornece o valor t. Quanto mais o valor t, melhor será o ajuste do modelo.
Também podemos encontrar o AIC e BIC usando as funções AIC() e BIC().

AIC(Linear_model)BIC(Linear_model)

Saída

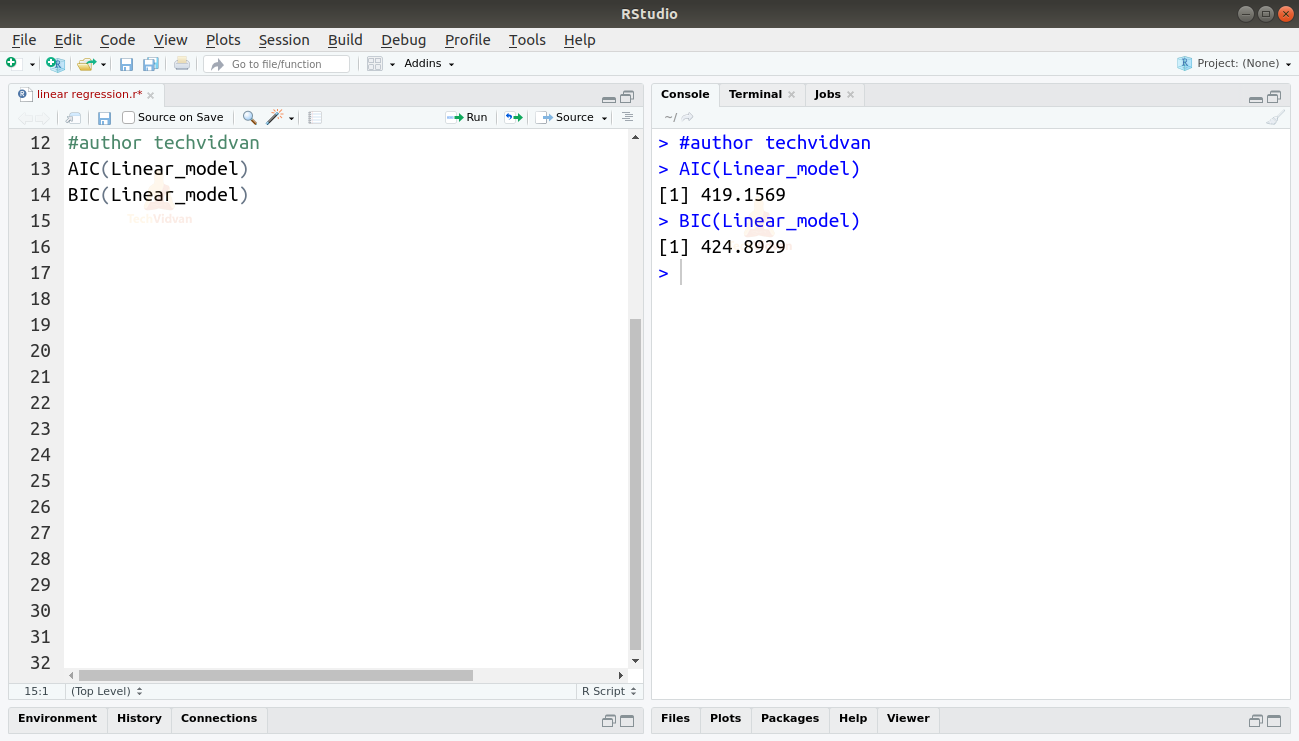
O modelo que resulta nas menores pontuações AIC e BIC é o mais preferido.

Resumo

Neste capítulo da série tutorial de R da TechVidvan, aprendemos sobre a regressão linear. Nós aprendemos sobre regressão linear simples e regressão linear múltipla. Depois estudamos várias medidas para avaliar a qualidade ou precisão do modelo, como o R2, R2 ajustado, erro padrão, estatística F, AIC, e BIC. Aprendemos então como implementar a regressão linear em R. Depois verificamos a qualidade do ajuste do modelo em R.

Partilhe a sua classificação no Google se você gostou do tutorial de Regressão Linear.