No gelado pequenos cristais de gelo redondos são importantes para uma textura suave e cremosa. Em geral, é importante que quanto mais rápido a taxa de congelamento, menor o tamanho do cristal de gelo. No entanto, para alguns materiais alimentares existe um limite superior para a taxa de congelação. Se o congelamento for demasiado rápido, são transmitidas tensões mecânicas ao material alimentar e pode ocorrer uma fractura por congelação. Em alguns casos, o processo de congelamento é usado para estruturar materiais, como o prato tradicional japonês de kori-tofu, ou andaimes como os usados na engenharia de tecidos biológicos. Alguns anos atrás a WUR, juntamente com a TU Delft e a Unilever, investigou o uso da liofilização para estruturar a sopa de vegetais. Aqui, o tamanho do cristal de gelo determina o tamanho do espaço do poro após a secagem, e ajuda na reidratação dos vegetais quando misturado com a sopa.
Relação entre o tamanho do cristal de gelo e a taxa de congelamento
Hence, da perspectiva da qualidade dos alimentos congelados, é importante ter um bom conhecimento sobre a relação entre o tamanho do cristal de gelo e a taxa de congelamento. No entanto, existem apenas algumas relações empíricas entre a taxa de congelamento e o tamanho do cristal de gelo. Além disso, para os alimentos fabricados existem alguns outros meios utilizados para controlar o tamanho do cristal de gelo, tais como os criopectantes como os açúcares e as proteínas anticongelantes. Isto indica que se pode esperar uma interacção entre a composição dos alimentos, a taxa de congelação e o tamanho do cristal de gelo, mas nas relações empíricas a dependência da composição dos alimentos está ausente. Portanto, a Food & Biobased Research envolveu um projeto de pesquisa voltado para uma compreensão mais teórica da relação entre taxa de congelamento, composição e tamanho do cristal de gelo usando simulações avançadas em computador.
Modelo de campo fase para crescimento do cristal de gelo
Para obter este detalhe de compreensão devemos mergulhar na faixa de micrometragem da microestrutura dos alimentos, onde cristais individuais de gelo são resolvidos no modelo de computador desenvolvido, onde o crescimento do cristal é modelado em função da composição da matriz. O método mais avançado neste campo é o modelo de campo de fase, que temos utilizado para descrever a estruturação de dispersões como espumas e emulsões, estabilizadas com emulsificantes. No método de campo de fase é possível modelar simultaneamente vários elementos individuais de dispersões, como gotículas de emulsão, bolhas de espuma e cristais. O método permite facilmente a ruptura e coalescência destes elementos dispersos.
A força do método reside na forma como trata a interface entre as fases dispersas e contínuas. Aqui, o método segue a proposta de um famoso físico holandês, vanderWaals, de incluir a interface em uma estrutura termodinâmica. Usando o método de campo de fases, construímos um modelo de computador para a descrição de cristais de gelo em uma solução de sacarose, cujo comportamento pode ser visto como representativo para sorvete3. Em pesquisas anteriores já esclarecemos a termodinâmica das soluções aquosas de sacarose4, e também a velocidade do transporte de água em solução de açúcar via difusão5. Assim, para estas propriedades materiais temos teorias preditivas disponíveis em função da concentração de sacarose para toda a faixa de 0 a 100%.
Freeze rate, composição e tamanho do cristal de gelo
Após termos desenvolvido o modelo computador, realizamos várias simulações computadorizadas para investigar a relação entre taxa de congelamento, composição e tamanho do cristal de gelo. Fizemos um zoom em uma pequena parte do material alimentar e semeamos vários núcleos para que os cristais de gelo crescessem. Esta parte do material alimentar foi então sujeita a uma gama de taxas de congelação. Foram feitas simulações para duas concentrações diferentes de sacarose – e uma multidão de diferentes posições aleatórias dos núcleos – a fim de obter algumas boas estatísticas.
Snapshots destas simulações em computador são mostrados na Figura 1. Os elementos dispersos a azul escuro são cristais individuais de gelo. A taxa de congelamento não é muito rápida, então podemos assumir que os cristais de gelo permanecem aproximadamente esféricos. Para entender os resultados da simulação é importante saber que os cristais de gelo não contêm açúcar, portanto o crescimento dos cristais de gelo implica no aumento das concentrações de açúcar na fase não congelada. O aumento da concentração de açúcar leva a um aumento do ponto de congelamento, deixando a matriz contínua descongelada.

Figure 1: Instantâneos do crescimento dos cristais de gelo em uma solução de açúcar obtidos através de simulações computadorizadas para diferentes taxas de congelamento (0,01, 0,03 e 0,10 K/s de cima para baixo) observadas em diferentes momentos (da esquerda para a direita). Observe a coalescência de vários cristais de gelo, especialmente na baixa taxa de congelamento (topo)
Alguns outros cristais de gelo podem se colidir uns com os outros, levando a um aumento da concentração de açúcar no líquido não congelado entre eles, levando à depressão do ponto de congelamento. Assim, é desenvolvida uma interface plana. Se a taxa de congelamento for muito lenta, os açúcares têm tempo para se difundirem para fora da zona de impacto e os cristais podem coalescer. Na fase inicial do congelamento, onde o aumento local da concentração de açúcar devido ao crescimento dos cristais de gelo é pequeno, há vários eventos de coalescência. Na fase posterior do congelamento, a matriz não congelada aproxima-se do estado vítreo – onde a difusão da água e do açúcar se detém e o crescimento do cristal de gelo pára.
A partir das simulações determinamos o tamanho médio dos cristais de gelo e traçamos este contra a taxa de congelamento imposta para duas concentrações diferentes de sacarose. Estes resultados são mostrados na Figura 2.
Dispersão concebível pode ser observada nos dados da simulação, devido à estocástica do processo de nucleação. Entretanto, ao executar muitas simulações, pode-se encaixar uma relação de potência confiável através dos dados, que são exibidos como as linhas que passam pelos pontos de dados na Figura 2 (página 00). O ajuste mostra que os expoentes da lei de potência são 0,31 e 0,18 para 10% e 15% de concentração inicial de açúcar, respectivamente. Nossa relação empírica anterior tem um expoente da lei de potência de 0,25, que foi assumido como sendo independente da composição. O fato de o valor empírico ser bastante próximo dos expoentes que encontramos via simulação é muito encorajador. Além disso, vale notar que o modelo de simulação não requereu nenhum ajuste de parâmetro, pois todas as propriedades materiais e termodinâmicas são conhecidas.
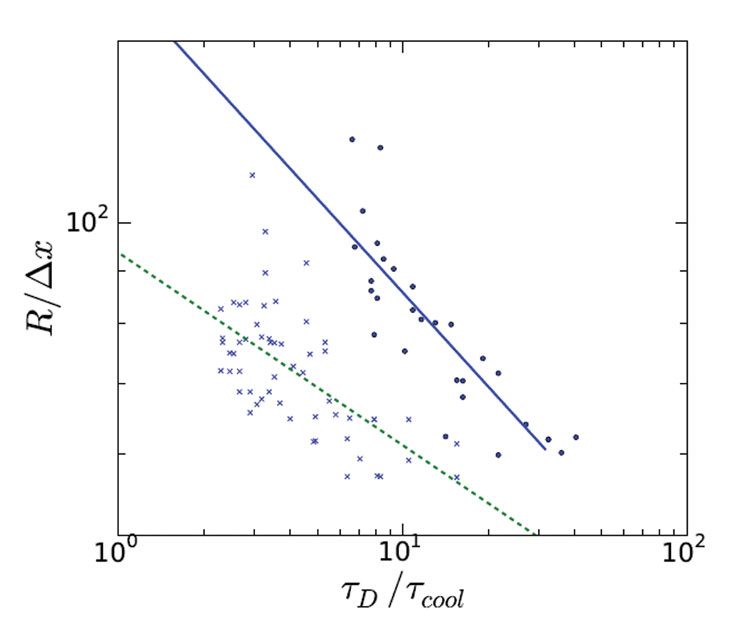
Figure 2: Tamanho médio do cristal de gelo versus a taxa de congelamento, para duas concentrações iniciais de açúcar diferentes (10% e 15%, indicadas por linha sólida e tracejada). O raio é medido em unidades da malha computacional, que é de cerca de 3 mícrons, e a taxa de congelamento 1/trigo é medida em termos da taxa de difusão de água 1/tD. (a 0,01K/s se tD/tcool=1) Os pontos indicam o tamanho médio de uma única simulação. As linhas representaram relações de potência, ajustadas aos dados da simulação
Das questões de qualidade alimentar para frutas e vegetais congelados
Alimento &Biobaseado Pesquisa conclui que o modelo tem um grande grau de realismo. Além disso, teorias preditivas semelhantes sobre material e propriedades termodinâmicas estão disponíveis para muitos outros materiais alimentares. Consequentemente, o modelo é, em princípio, aplicável a uma multiplicidade de outros materiais alimentares. Nesta base, lançámos um novo projecto de investigação que continua a desenvolver e adaptar o modelo a materiais alimentares congelados com uma estrutura celular para investigar questões de qualidade dos alimentos congelados para frutas e vegetais. O modelo de campo de fase será incorporado num modelo multiescala – porque nos produtos alimentares surgirão diferenças locais na taxa de congelamento – que devem ser resolvidas com uma abordagem avançada, onde o perfil de temperatura é computado na escala do produto, e o crescimento do cristal de gelo na microescala. O modelo de computador em macroscala chamará o modelo em microescala várias vezes para uma multiplicidade de locais. O modelo em microescala irá reportar a fração de gelo local, enquanto o modelo em macroscala irá emitir o gradiente de temperatura aplicado ao modelo em microescala.
Neste novo projeto, Food & Biobased Research, nós iremos focar não apenas no passo inicial de congelamento, mas também no armazenamento congelado. Durante o armazenamento podem ocorrer flutuações de temperatura devido ao resfriamento mecânico, ou abertura e fechamento de portas. Assume-se que estas flutuações de temperatura permitem que os cristais de gelo cresçam ainda mais, o que é desvantajoso para a qualidade do produto6. Nosso objetivo é investigar se a redução da temperatura de armazenamento torna o alimento menos sensível às flutuações de temperatura, e até mesmo se a redução no uso de energia pode ser obtida. Além disso, mesmo onde a temperatura de armazenamento é razoavelmente constante, ainda há um engrossamento da distribuição dos cristais de gelo que ocorre durante o armazenamento nas condições convencionais de -18oC. Isto é demonstrado na comparação de alimentos congelados através do congelamento por jacto de ar e do congelamento por deslocamento de pressão (PSF). Inicialmente, o tamanho do cristal de gelo obtido via PSF é muito menor do que o obtido via congelamento por jacto de ar convencional. No entanto, após várias semanas de armazenamento é encontrada pouca diferença na distribuição final do tamanho do cristal de gelo, o que indica que o congelamento ocorreu durante o armazenamento de alimentos com PSF7.
Em resumo, o novo modelo de simulação é uma ferramenta essencial para mergulhar em possíveis meios para a indústria de alimentos congelados controlar a textura dos alimentos congelados e o tamanho do cristal de gelo, em áreas como 1) formulação do produto, 2) condições de processamento e taxa de congelamento. Conhecendo o impacto da formulação e do processamento na qualidade dos alimentos congelados, novas estratégias para o armazenamento de alimentos congelados podem ser avaliadas devido ao seu impacto tanto na qualidade do produto quanto na economia de energia.
- Voda, A., Homan, N., Witek, M., Duijster, A., van Dalen, G., van der Sman, R., Nijsse, J, van Vliet, L. Van As, H. & van Duynhoven, J. (2012). O impacto da liofilização na microestrutura e propriedades de reidratação da cenoura. Food Research International, 49(2), 687-693
- van der Sman, R. G. M., Voda, A., van Dalen, G., & Duijster, A. (2013). Espaçamento entre cristais de gelo em alimentos congelados. Journal of Food Engineering, 116(2), 622-626
- van der Sman, R. G. M. (2016). Simulações de fase de crescimento de cristais de gelo em soluções açucaradas. International Journal of Heat and Mass Transfer, 95, 153-161
- van der Sman, R. G. M., & Meinders, M. B. J. (2011). Predição do diagrama de estado de misturas de amido com água usando a teoria do volume livre de Flory-Huggins. Soft Matter, 7(2), 429-442
- van der Sman, R. G. M., & Meinders, M. B. J. (2013). Difusividade de umidade em materiais alimentares. Food chemistry, 138(2), 1265-1274
- Regand, A & Goff HD. “Estrutura e recristalização de gelo em sistemas de modelos de sorvete estabilizado congelado”. Food Hydrocolloids1 (2003): 95-102
- Fernández PP, Otero L, Martino MM ,Molina-García AD, & Sanz PD “High-pressure shift freezing: recrystallization during storage” European Food Research and Technology 5 (2008): 1367-1377
Sobre o autor
Ruud van der Sman tem um MSc em Física Aplicada na Delft University of Technology e um PhD em Engenharia Agrícola pela Wageningen University. Ele trabalha como pesquisador sênior na área de Alimentos & Pesquisa Biobaseada, e professor assistente em tempo parcial na Engenharia de Processos Alimentares – ambos parte de Wageningen UR (Universidade & Centro de Pesquisa). Os seus interesses de investigação compreendem a física da matéria mole dos materiais alimentares, a modelação informática da estruturação dos alimentos à escala micrométrica, e a modelação fisiológica. A sua especialização em carne compreende a termodinâmica da capacidade de retenção de água, transferência de calor e massa e fisiologia post-mortem. www.wageningenur.nl/en/fbr