Um metamaterial electromagnético afecta as ondas electromagnéticas que colidem ou interagem com as suas características estruturais, que são menores do que o comprimento de onda. Para se comportar como um material homogêneo descrito com precisão por um índice de refração efetivo, suas características devem ser muito menores que o comprimento de onda.

Para radiação de microondas, as características estão na ordem de milímetros. Os metamateriais de freqüência de microondas são geralmente construídos como matrizes de elementos condutores de eletricidade (como laços de fios) que possuem características indutivas e capacitivas adequadas. Muitos metamateriais de microondas utilizam ressonadores de anel dividido.

Metamateriais fotônicos são estruturados na escala nanométrica e manipulam a luz em freqüências ópticas. Cristais fotônicos e superfícies seletivas de freqüência, como grades difrativas, espelhos dielétricos e revestimentos ópticos apresentam semelhanças com os metamateriais estruturados em sub-comprimento de onda. Contudo, estes são geralmente considerados distintos dos metamateriais, uma vez que a sua função resulta de difração ou interferência e, portanto, não pode ser aproximada como um material homogêneo. No entanto, estruturas materiais como os cristais fotônicos são eficazes no espectro de luz visível. O meio do espectro visível tem um comprimento de onda de aproximadamente 560 nm (para a luz solar). As estruturas cristalinas fotônicas são geralmente metade deste tamanho ou menores, ou seja, <280 nm.

Metamateriais plásticos utilizam plasmões de superfície, que são pacotes de carga elétrica que oscilam coletivamente nas superfícies dos metais em freqüências ópticas.

Superfícies seletivas de freqüência (FSS) podem exibir características de sub-comprimento de onda e são conhecidas várias vezes como condutores magnéticos artificiais (AMC) ou Superfícies de Alta Impedância (HIS). Os FSS apresentam características indutivas e capacitivas que estão directamente relacionadas com a sua estrutura de sub-comprimento de onda.

Metamateriais eletromagnéticos podem ser divididos em diferentes classes, como segue:

Índice de refração negativoEditar

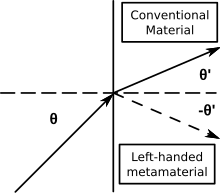
Metamateriais de índice negativo (NIM) são caracterizados por um índice negativo de refração. Outros termos para NIMs incluem “mídia canhota”, “mídia com índice de refração negativo”, e “mídia com ondas para trás”. MNE onde o índice negativo de refração surge da permissividade e permeabilidade negativas simultâneas são também conhecidos como metamateriais negativos duplos ou materiais negativos duplos (DNG).

Sumindo um material bem aproximado por uma permissividade e permeabilidade reais, a relação entre permissividade ϵ r {\displaystyle \epsilon _{r}}

, permeabilidade μ r {\i}displaystyle {\i}mu _{r}}

e índice refractivo n é dado por n = ± ϵ r μ r {\i1}displaystyle {\i}scriptstyle n=pm {\i}epsilon _{\i1}mathrm mu _mu _mathrm _r} }}}}

. Todos os materiais transparentes não-metamateriais conhecidos (vidro, água, …) possuem positivo ϵ r {\i1}displaystyle {\i}epsilon _{\i}

e μ r {\i}displaystyle _{r}}

. Por convenção, a raiz quadrada positiva é usada para o n. No entanto, alguns metamateriais artificiais têm ϵ r {\i1}epsilon _{\i}

e μ r < 0 {\i}displaystyle {\i}mu _{r}<0}

. Porque o produto ϵ r μ r {\i1}displaystyle {\i}epsilon _{\i}mu _{\i}}

é positivo, n é real. Em tais circunstâncias, é necessário tomar a raiz quadrada negativa para n. Quando ambos ϵ r {\i1}epsilon _{\i}

e μ r {\i}displaystyle _{r}}

são positivos (negativos), as ondas viajam na direcção da frente (para trás). Ondas electromagnéticas não se podem propagar em materiais com ϵ r {\i} {\i1}epsilon _{\i}}

e μ r {\i}displaystyle _{r}}

de sinal oposto à medida que o índice refractivo se torna imaginário. Tais materiais são opacos para a radiação eletromagnética e exemplos incluem materiais plasmônicos como metais (ouro, prata, …).

As considerações anteriores são simplistas para materiais reais, que devem ter valoração complexa ϵ r {\i1}epsilon _{\i}

>

e μ r {\i}displaystyle {\i}mu _{r}}

. As verdadeiras partes de ambos ϵ r r {\i1}displaystyle {\i}epsilon _{\i}

e μ r {\i}displaystyle _{r}}

não tem de ser negativo para que um material passivo apresente uma refracção negativa. De facto, um índice de refracção negativo para ondas circularmente polarizadas também pode surgir da quiralidade. Metamateriais com n negativo têm numerosas propriedades interessantes:

• A lei de Snell (n1sinθ1 = n2sinθ2) ainda descreve a refracção, mas como n2 é negativo, os raios incidentes e refractários estão no mesmo lado da superfície normal numa interface de materiais de índice positivo e negativo.
• A radiação de Cherenkov aponta para o outro lado.
• O vetor Poynting de tempo médio é antiparalelo à velocidade de fase. No entanto, para que as ondas (energia) se propaguem, a -µ deve ser emparelhada com a -ε de modo a satisfazer a dependência do número de ondas dos parâmetros do material k c = ω μ ϵ {\displaystyle kc===omega {\sqrt {\mu {\epsilon }}}
  

  .

O índice negativo de refração deriva matematicamente do trigêmeo vetorial E, H e k.

Para ondas planas propagando em metamateriais eletromagnéticos, o campo elétrico, campo magnético e vetor de onda seguem uma regra da esquerda, o inverso do comportamento dos materiais ópticos convencionais.

Até à data, apenas os metamateriais apresentam um índice de refracção negativo.

Edição negativa única

Metamateriais negativos únicos (SNG) têm uma permissividade relativa negativa (εr) ou uma permeabilidade relativa negativa (µr), mas não ambas. Eles atuam como metamateriais quando combinados com um SNG diferente e complementar, atuando conjuntamente como um DNG.

Epsilon negative media (ENG) exibe um negativo εr enquanto µr é positivo. Muitos plasmas exibem esta característica. Por exemplo, metais nobres como ouro ou prata são ENG nos espectros infravermelhos e visíveis.

Mu-negativos (MNG) exibem um positivo εr e um negativo µr. Os materiais girotrópicos ou giromagnéticos exibem esta característica. Um material girotrópico é aquele que foi alterado pela presença de um campo magnético quasistático, permitindo um efeito magneto-óptico. Um efeito magneto-óptico é um fenômeno no qual uma onda eletromagnética se propaga através desse meio. Em tal material, polarizações elípticas giratórias para a esquerda e para a direita podem propagar-se a diferentes velocidades. Quando a luz é transmitida através de uma camada de material magneto-óptico, o resultado é chamado efeito Faraday: o plano de polarização pode ser girado, formando um rotador Faraday. Os resultados de tal reflexão são conhecidos como efeito Kerr magneto-óptico (não confundir com o efeito Kerr não-linear). Dois materiais girotrópicos com sentidos de rotação invertidos das duas polarizações principais são chamados isômeros ópticos.

Juntar uma placa de material ENG e uma placa de material MNG resultou em propriedades tais como ressonâncias, tunelização anômala, transparência e reflexão zero. Tal como os materiais de índice negativo, os SNG são inatamente dispersivos, pelo que o seu εr, µr e índice de refracção n, são função da frequência.

HyperbolicEdit

Hyperbolic metamaterials (HMMs) comportam-se como um metal para determinada polarização ou direcção de propagação da luz e comportam-se como um dieléctrico para o outro devido aos componentes negativos e positivos do tensor de permissividade, dando uma anisotropia extrema. A relação de dispersão do material no espaço vectorial das ondas forma um hiperbolóide e por isso é chamado de metamaterial hiperbólico. A anisotropia extrema dos HMMs leva à propagação direcional da luz dentro e sobre a superfície. HMMs têm mostrado várias aplicações potenciais, tais como sensoriamento, imagens, direção de sinais ópticos, efeitos de ressonância plasmonar melhorados.

BandgapEdit

Electromagnetic bandgap metamaterials (EBG ou EBM) controlam a propagação da luz. Isto é realizado com cristais fotônicos (PC) ou materiais canhotos (LHM). Os PCs podem proibir completamente a propagação da luz. Ambas as classes podem permitir que a luz se propague em direções específicas e projetadas e ambas podem ser projetadas com faixas de faixa nas freqüências desejadas. O tamanho do período dos EBGs é uma fração apreciável do comprimento de onda, criando interferência construtiva e destrutiva.

PC distinguem-se das estruturas de sub-comprimento de onda, como os metamateriais sintonizáveis, porque o PC deriva suas propriedades de suas características de bandgap. Os PCs são dimensionados para combinar com o comprimento de onda da luz, versus outros metamateriais que expõem a estrutura de sub-comprimento de onda. Além disso, os PCs funcionam difratando a luz. Em contraste, os metamateriais não usam difração.

PCs têm inclusões periódicas que inibem a propagação de ondas devido à interferência destrutiva da dispersão das inclusões. A propriedade de bandgap fotônico dos PCs faz deles o análogo eletromagnético dos cristais semicondutores eletrônicos.

EBGs têm o objetivo de criar estruturas dielétricas de alta qualidade, baixa perda, periódicas e dielétricas. Um EBG afeta os fótons da mesma forma que os materiais semicondutores afetam os elétrons. Os PCs são o material de bandgap perfeito, porque não permitem a propagação da luz. Cada unidade da estrutura periódica prescrita age como um átomo, embora de tamanho muito maior.

EBGs são projetados para evitar a propagação de uma largura de banda alocada de freqüências, para certos ângulos de chegada e polarizações. Várias geometrias e estruturas foram propostas para fabricar as propriedades especiais dos EBG. Na prática é impossível construir um dispositivo EBG sem falhas.

EBGs foram fabricados para frequências que vão desde alguns gigahertz (GHz) a alguns terahertz (THz), rádio, microondas e regiões de frequências de infravermelhos médios. Os desenvolvimentos da aplicação EBG incluem uma linha de transmissão, pilhas de madeira feitas de barras dielétricas quadradas e vários tipos diferentes de antenas de baixo ganho.

Medio positivo duploEditar

Meios positivos duplos (DPS) ocorrem na natureza, tais como dielétricos naturais. A permissividade e a permeabilidade magnética são ambas positivas e a propagação das ondas é na direcção da frente. Foram fabricados materiais artificiais que combinam propriedades DPS, ENG e MNG.

Edita Bi-isotrópica e bianisotrópica

Categorizando metamateriais em duplo ou único negativo, ou duplo positivo, normalmente assume que o metamaterial tem respostas elétricas e magnéticas independentes descritas por ε e µ. Entretanto, em muitos casos, o campo elétrico causa polarização magnética, enquanto o campo magnético induz polarização elétrica, conhecida como acoplamento magnetoelétrico. Tais meios são denotados como bi-isotrópicos. Meios que apresentam acoplamento magnetoelétrico e que são anisotrópicos (que é o caso de muitas estruturas de metamateriais), são referidos como bi-anisotrópicos.

Quatro parâmetros materiais são intrínsecos ao acoplamento magnetoelétrico de meios bi-isotrópicos. Eles são as intensidades de campo elétrico (E) e magnético (H), e as densidades de fluxo elétrico (D) e magnético (B). Estes parâmetros são ε, µ, κ e χ ou permutabilidade, permeabilidade, resistência da quiralidade, e o parâmetro Tellegen, respectivamente. Neste tipo de material, os parâmetros do material não variam com as alterações ao longo de um sistema de coordenadas rotacionadas. Neste sentido eles são invariantes ou escalares.

Os parâmetros magnetoelétricos intrínsecos, κ e χ, afetam a fase da onda. O efeito do parâmetro quiralidade é a divisão do índice de refração. Em meios isotrópicos isto resulta na propagação da onda apenas se ε e µ tiverem o mesmo sinal. Em meios bi-isotrópicos com χ assumido como sendo zero, e κ um valor não zero, aparecem resultados diferentes. Pode ocorrer uma onda para trás ou uma onda para a frente. Alternativamente, podem ocorrer duas ondas para frente ou duas ondas para trás, dependendo da força do parâmetro de quiralidade.

No caso geral, as relações constitutivas para materiais bi-anisotrópicos são D = ϵ E + ξ H , {\displaystyle \mathbf {D} =epsilon \mathbf {E} +\i {H} ,} B = ζ E + μ H , {\i1}displaystyle {B} =zeta {\i}mathbf {E} +\Mu {H},}

onde ϵ {\i1}displaystyleepsilon

e μ {\i1}displaystyle

são os tensores de permissividade e permeabilidade, respectivamente, enquanto que ξ {\displaystyle \xi}

e ζ {\i1}displaystyle {\i}

são os dois tensores magnetoeléctricos. Se o meio é recíproco, a permissividade e a permeabilidade são tensores simétricos, e ξ = – ζ T = – i κ T {\displaystyle \xi =–\zeta ^{T}=-i\kappa ^{T}}

, onde κ {\i1}displaystyle {\i}

é o tensor quiral que descreve a resposta electromagnética quiral e a resposta magnético-eléctrica recíproca. O tensor quiral pode ser expresso como κ = 1 3 tr ( κ ) I + N + J {\i1}{\i1}kappa ={\i1}frac {\i}{\i}{\i}{\i1}operatorname {\i} (kappa )I+N+J}

, onde tr ( κ ) {\i1}displaystyle {\i}displaystyle {tr}operatorname (kappa )}

é o traço de κ {\i1}displaystyle {\i}kappa

, I é a matriz de identidade, N é um tensor simétrico sem traços, e J é um tensor antissimétrico. Tal decomposição permite-nos classificar a resposta bianisotrópica recíproca e podemos identificar as três classes principais seguintes: (i) chiral media ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\i1}displaystyle {\i}operatorname {tr} (kappa )neq 0,Nneq 0,J=0}

), (ii) pseudo-espiral media ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\i1}displaystyle {\i}operatorname {tr} (\kappa )=0,N\neq 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle {\displaystyle \displaystorname {tr} (\kappa )=0,N=0,J\neq 0}

).

ChiralEdit

Handedness of metamaterials is a potential source of confusion as the metamaterial literature include two conflicting uses of the terms left- and right-handed. O primeiro refere-se a uma das duas ondas circularmente polarizadas que são os modos de propagação em meios quirais. A segunda refere-se ao trigêmeo do campo elétrico, campo magnético e vetor Poynting que surgem em meios de índice de refração negativos, que na maioria dos casos não são quirais.

Generalmente uma resposta eletromagnética quiral e/ou bianisotrópica é uma conseqüência da quiralidade geométrica 3D: os metamateriais quirais 3D são compostos pela incorporação de estruturas quirais 3D em um meio hospedeiro e mostram efeitos de polarização relacionados à quiralidade, tais como atividade óptica e dicroísmo circular. O conceito de quiralidade 2D também existe e diz-se que um objeto plano é quiral se não puder ser sobreposto à sua imagem espelhada a menos que seja levantado do plano. Metamateriais 2D-virais que são anisotrópicos e perdidos têm sido observados para exibir transmissão direcionalmente assimétrica (reflexão, absorção) de ondas circularmente polarizadas devido ao dichrosim de conversão circular. Por outro lado, a resposta bianisotrópica pode surgir de estruturas geométricas achíricas que não possuem quiralidade intrínseca 2D ou 3D. Plum e colegas investigaram o acoplamento magnetoelétrico devido à quiralidade extrínseca, onde a disposição de uma estrutura (achiral) juntamente com o vetor de onda de radiação é diferente de sua imagem espelhada, e observaram grande atividade óptica linear sintonizável, atividade óptica não linear, atividade óptica especular e dicroísmo de conversão circular. Rizza et al. sugeriram metamateriais quirais 1D onde o tensor quiral efetivo não está desaparecendo se o sistema for geometricamente quiral unidimensional (a imagem espelhada de toda a estrutura não pode ser sobreposta a ela usando translações sem rotações).

3D metamateriais quirais são construídos a partir de materiais quirais ou ressonadores em que o parâmetro de quiralidade efetivo κ {\displaystyle \kappa }

é não-zero. As propriedades de propagação das ondas em tais metamateriais quirais demonstram que a refração negativa pode ser realizada em metamateriais com uma forte quiralidade e positiva ϵ r {\i1}displaystyle {\i}epsilon _{r}}

e μ r {\i1}displaystyle {\i}mu _{\i}

. Isto é porque o índice de refracção n {\i1}displaystyle n}

tem valores distintos para ondas polarizadas circularmente à esquerda e à direita, dados por

n = ± ϵ r μ r ± κ {\displaystyle n==pm {\sqrt {\r}epsilon _{\r}}mu _{\r}pm {\r}kappa }

Pode ser visto que um índice negativo ocorrerá para uma polarização se κ {\i}displaystyle {\i}kappa

> ϵ r μ r {\i1}displaystyle {\i}{\i}epsilon _{\i}mu _{\i}}}}

. Neste caso, não é necessário que um ou outro, ou ambos, ϵ r r {\i1}displaystyle {\i}epsilon _{\i}

e μ r {\i1}displaystyle {\i}mu _{\i}

ser negativo para propagação de ondas para trás. Um índice de refração negativo devido à quiralidade foi observado pela primeira vez simultânea e independentemente por Plum et al. e Zhang et al. em 2009.

FSS basedEdit

Metamateriais de superfície seletivos de freqüência bloqueiam sinais em uma banda de onda e passam aqueles em outra banda de onda. Eles se tornaram uma alternativa aos metamateriais de freqüência fixa. Eles permitem mudanças opcionais de freqüência em um único meio, ao invés das limitações restritivas de uma resposta de freqüência fixa.