- Come un adolescente ha inventato un nuovo ramo della matematica per risolvere una lunga questione aperta sulle equazioni
- Radici germinanti e simmetria
- La dimensione del quintico
- Campi e Automorfismi
- Due esempi di grado 3
- Esempio 2
- Gruppi
- Visualizzare i gruppi
- Tabelle di Cayley
- Grafico di Caylay
- Usi dei gruppi
- Torna ai campi
- Sottocampi e sottogruppi
- Campi fissi
- Schizzo del teorema fondamentale della teoria di Galois
- Quotiente
- Radicali
- Sottogruppi del quintico
- Trisecting the angle
- Risolvere la quintica generale
Come un adolescente ha inventato un nuovo ramo della matematica per risolvere una lunga questione aperta sulle equazioni

Forse sapete che per risolvere un’equazione di grado 2, ax²+bx+c = 0, si usa la formula quadratica.
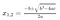
Esistono formule simili per le equazioni di grado 3 e 4, ma mancano misteriosamente per il 5 o più. Più specificamente, sembra che non possiamo costruire le soluzioni della quintica (equazione di grado 5) o superiore usando solo addizione, sottrazione, moltiplicazione, divisione e radicali (radici quadrate, radici al cubo, ecc.). Perché, cosa c’è di così speciale nel numero 5? Queste erano domande che ossessionavano il giovane francese Evariste Galois all’inizio del 1800, e la notte prima di essere ferito mortalmente in un duello, scrisse una teoria di un nuovo oggetto matematico chiamato “gruppo” che risolve la questione in un modo sorprendentemente elegante.
Ecco come ha fatto.
L’insieme delle radici di diverse equazioni sono di diversa complessità. Alcuni insiemi sono così complessi che non possono essere espressi usando solo oggetti semplici come i radicali. Ma come possiamo misurare la complessità delle radici se non possiamo nemmeno calcolarle, e quale misura di complessità dovremmo usare?
Radici germinanti e simmetria
La risposta sta nella simmetria delle radici.
Simmetria delle radici vi chiederete, cosa ha a che fare con tutto ciò? Che cosa significa?
Tracciamo le radici di due equazioni e vediamo se riusciamo a capirci qualcosa:

Si dice che la sinistra è meno simmetrica della destra. Questo potrebbe sorprendervi, perché nel senso colloquiale della parola, simmetrico è di solito usato se si può riflettere o ruotare l’oggetto senza cambiare il suo aspetto. In questo senso, l’immagine di sinistra sembra più simmetrica.
Per esempio: La stella è più simmetrica del cuore, perché oltre a rifletterlo, si può anche ruotarlo.

Ma nel nostro caso, prenderemo una visione più generale delle simmetrie. Non ci stiamo limitando solo a riflessioni e rotazioni, qualsiasi funzione che trasforma l’oggetto senza cambiarne l’aspetto è un gioco lecito. Nel caso delle radici, questo significa che qualsiasi funzione che cambia (permuta) le radici in qualsiasi modo è valida. Più funzioni significa più simmetrico.
Si scopre che nel caso destro, ci sono funzioni per permutare tutte le radici in qualsiasi ordine concepibile, fino a 5!=120, quindi è altamente simmetrico. Ma nel caso sinistro, se scambiamo r₂↔r₄ usando la trasformazione i↔-i scambiamo necessariamente anche r₁↔r₅. Questo ci limita, e quindi non sono possibili tutte le permutazioni concepibili. È meno simmetrico.
Le funzioni che permutano le radici si chiamano “Automorfismi”, e se raggruppiamo questi automorfismi otteniamo quello che si chiama un “Gruppo” (tornerò più avanti su definizioni migliori di automorfismi e gruppi).
Questo significa che il gruppo che rappresenta le simmetrie delle radici è più grande e complesso nel caso giusto. Infatti, il gruppo nel caso giusto è così complesso che le radici non possono essere descritte usando i radicali.
Come facciamo a sapere quanto è complesso un gruppo? Per capirlo abbiamo bisogno di un po’ più di teoria.
La dimensione del quintico
Prima di tutto, diamo un’occhiata alla dimensione di un gruppo. Come faccio a sapere che ci sono delle quintine che hanno un gruppo grande 5!
Una quintica generale normalmente assomiglia a questa:
x⁵+ax⁴+bx³+cx²+dx+e=0
Ma se adottiamo un approccio più “root-centrico” possiamo dire che assomiglia a questa:
(x-r₁)(x-r₂)(x-r₃)(x-r₄)(x-r₅)=
x⁵-(r₁+r₂+r₃+r₅)x⁴+
(r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅)x³…- r₁r₂r₃r₄r₅=0
Ovvero, la costante a,b,c,d,e nella prima equazione è sostituita da una combinazione simmetrica delle radici:
r₁+r₂+r₃+r₄+r₅=a
r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅=b
(c e d omessi per brevità)
r₁r₂r₃r₄r₅ = e
Osservando tutti i termini in dettaglio, si scopre che l’interscambio delle radici non influisce sull’equazione (provate per esempio per b sopra). Questo è vero per polinomi di qualsiasi grado. Poiché siamo in grado di scambiare tutte le radici, possiamo trarre la conclusione che il gruppo di simmetria per questo quintico generale è in effetti tutte le permutazioni, chiamato anche S₅ (il gruppo simmetrico di ordine 5).
Campi e Automorfismi
Ora espanderemo un po’ la nostra definizione di automorfismi, poiché essi sono più che semplici funzioni che permutano le radici. Nel processo dobbiamo introdurre qualcosa chiamato “campi”. Perché dovremmo volerlo fare, direte voi? La ragione è che mentre lavorare con le radici e le loro permutazioni è divertente, è un po’ più facile lavorare con i campi e i loro automorfismi. Sono esattamente le stesse funzioni, non preoccupatevi, solo un altro modo di vederle.
Quindi, se l’equazione è, diciamo x²-2=0, invece di lavorare con le radici, r₁=√2, r₂=-√2 introdurremo il campo Q(√2). Si tratta di tutti i numeri razionali Q con l’aggiunta di √2. √2 è chiamato “estensione del campo”. Si presenta così: a+b√2 a,b∈Q. Per poter descrivere la radice dell’equazione abbiamo bisogno del campo Q(√2). Per ogni estensione del campo (e anche altri oggetti matematici) abbiamo un mucchio di funzioni, σₙ, che mandano un numero ad un altro numero unico nello stesso campo e seguono la condizione σ(a+b)=σ(a)+σ(b) e σ(ab)=σ(a)σ(b). σ è una funzione dell’estensione e non tocca il campo sottostante Q. Queste funzioni sono chiamate automorfismi. Per inciso, essi permutano anche le radici. Questo perché per la radice r:
r⁵+ar⁴+br³+cr²+dr+e=0⟹
σ(r⁵+ar⁴+br³+cr²+dr+e)=σ(0)⟹
σ(r)⁵+aσ(r)⁴+bσ(r)³+cσ(r)²+dσ(r)+e=0 (poiché σ non tocca Q (dove a, b, c, d,e vive))
Questo significa che anche σ(r) è una soluzione dell’equazione. E poiché:
σ(r₁)-σ(r₂)=σ(r₁)+σ(-1)σ(r₂)=σ(r₁-r₂)≠0
le radici sono distinte, quindi ne abbiamo 5, che devono essere le 5 originali. Quindi σ deve permutare le radici.
Ovviamente, questo funziona per un’equazione di qualsiasi grado.
Pertanto:
- Abbiamo la nostra equazione.
- Quell’equazione ha un campo che potrebbe contenere un’estensione di alcuni radicali
- Quell’estensione del campo ha un gruppo, che è una collezione di tutti i suoi automorfismi.
Due esempi di grado 3
Equazione: x³-x²-2x+2=0
Le radici sono (1,√2,-√2) (puoi verificarlo tu stesso semplicemente inserendole), quindi il campo deve essere Q(√2)
Scrivendo tutti i modi in cui possiamo pensare di permutare le radici (e significa permutazione di identità, non fa nulla):
(e)
(√2↔-√2)
(1↔√2)
(1↔-√2)
(√2→-√2 e 1→√2)
(√2↔-√2 e 1↔-√2)
Facciamo una prova: Sia (√2↔-√2) σ₁:
σ₁(√2+-√2)=σ₁(0)=0=σ₁(√2)+σ₁(-√2)
σ₁((√2)(-√2))=σ₁(-2)=-2=σ₁(√2)σ₁(-√2)
Fin qui tutto bene. Un altro.
Lascia che (1↔√2) sia σ₂:
σ₂(√2+-√2)=σ₂(0)=0 ≠ σ₂(√2)+σ₂(-√2)=1+-√2
σ₂((√2)(-√2))=2 ≠ σ₂(√2)σ₂(-√2)=1(-√2)
Apparentemente σ₂ non è un automorfismo, quindi dovremo scartarlo. L’altro σ incontra problemi simili, gli unici che rimangono sono e e σ₁. Questo è chiamato il gruppo ciclico C₂ poiché possiamo solo permutare in un cerchio (un cerchio molto piccolo in questo caso).
Esempio 2
Equazione: x³-2=0
Le radici sono
quindi il campo deve essere

utilizzando ζ per brevità. Ecco come appare:
Si può giocare un po’ con le permutazioni delle radici e si noterà subito che in questo caso sono tutti automorfismi. Così ci sono 3! automorfismi, che sono tutte le permutazioni delle radici, quindi il gruppo deve essere S₃.
Un’altra cosa divertente da notare sull’immagine sopra è che sembra un triangolo equilatero e che gli automorfismi corrispondono esattamente alla rotazione e alla riflessione del triangolo. Se gli automorfismi corrispondono alle simmetrie di un poligono regolare in questo modo, il gruppo è chiamato “gruppo Diedrico”. In questo caso D₃. Di solito il gruppo di tutte le permutazioni Sₙ non è lo stesso del gruppo diedro Dₙ, ma nel caso di n=3 lo è.
Gruppi
Questo sembra essere un buon posto per passare ad una discussione più lunga sui gruppi. Dunque, i gruppi sono iniziati come collezioni di permutazioni di radici, ma possono anche essere visti come collezioni di automorfismi, o rotazioni e riflessioni di oggetti geometrici simmetrici. Qualsiasi collezione di funzioni che cambia un oggetto in modo tale che sembri lo stesso può essere considerato un gruppo. Ma possiamo guardare le trasformazioni stesse senza preoccuparci dell’oggetto simmetrico su cui agiscono. Allo stesso modo in cui non ci preoccupiamo delle pile di mele quando facciamo l’aritmetica, semplicemente seguiamo le regole, allo stesso modo possiamo definire alcune regole che le trasformazioni di un gruppo seguono, e usarle.
Le regole sono qualcosa del genere:
Se facciamo prima una trasformazione, e poi un’altra, otterremo una terza trasformazione che è ancora nel gruppo. Per esempio, il gruppo C₄ è il gruppo di tutte le rotazioni che si possono fare su un quadrato. Se a ruota di 90∘, b ruota di 180∘ e c ruota di 270∘ allora a∗b=c. Dove ∗ significa, prima fai b poi a, comunemente chiamata moltiplicazione poiché è (più o meno) simile alla moltiplicazione dei numeri. Secondo la regola precedente, c deve essere nel gruppo. Questo si chiama chiusura.
Ci deve essere un elemento identico (e) che non fa nulla.
Per ogni elemento ci deve essere un inverso di quell’elemento.
Ora possiamo studiare le caratteristiche di diversi gruppi senza doverci preoccupare di radici o poligoni.
Visualizzare i gruppi
Due modi divertenti per visualizzare i gruppi sono:
Tabelle di Cayley
Questa è la tabella di Caylay per un triangolo equilatero, il gruppo D₃. Sono tutti gli elementi del gruppo e quali elementi otteniamo quando li moltiplichiamo. Per esempio, se facciamo prima una rotazione di 120∘ (r) e poi la stessa rotazione di nuovo otteniamo una rotazione di 240∘ rr=r² come si può vedere nella tabella. Se facciamo una rotazione di 120∘ rotazione-flip rf e una r ci ritroviamo con solo un flip. Nota come gli elementi f e r non si commutano. Un gruppo in cui gli elementi sono commutati è chiamato un gruppo abeliano.
Questa particolare tabella è ancora molto simmetrica però, ma non è necessario che sia così. Qualsiasi rimescolamento degli elementi che segua le regole è valido.
Grafico di Caylay
Quello sopra è il grafico D₃ Caylay. Qui gli elementi sono visualizzati in modo da mostrare come arrivare da un elemento al successivo, dove i bordi sono le operazioni. In questo caso è necessaria una rotazione di 120∘ e un flip, questi (r e f) sono anche chiamati i generatori del gruppo perché si può generare l’intero gruppo con loro, partendo dall’elemento identità.
Usi dei gruppi

I gruppi tendono ad essere utili ovunque ci sia simmetria. Per esempio, i gruppi di carte da parati sono usati per descrivere carte da parati simmetriche. Ci sono alcuni sfondi che possono essere ruotati di 180∘ e alcuni sfondi che possono essere riflessi e alcuni dove possiamo fare entrambi, e così via. Si è scoperto che ce ne sono solo 17, quindi è un modo pulito di classificare gli sfondi.
Gli sfondi di cui sopra appartengono entrambi a un gruppo chiamato p6m.
Un altro, più sorprendente, uso dei gruppi è nella fisica. Sembra che le leggi della natura seguano certe simmetrie. Per esempio, se si trasforma la seconda legge di Newton F=ma, 10 minuti nel futuro è ancora la stessa. Il fatto che le leggi della natura non cambino da un giorno all’altro sembra indicare che sono simmetriche rispetto alla trasformazione del tempo. Non cambiano nemmeno da un luogo all’altro, quindi anche le trasformazioni nello spazio sono permesse. Poiché è possibile trasformare il tempo e lo spazio in pezzi arbitrariamente piccoli o grandi, i gruppi che li descrivono, i gruppi di Lie, contengono una quantità infinita di elementi.
È interessante notare che queste simmetrie sono tutte legate a una legge di conservazione ciascuna. La simmetria temporale comporta la conservazione dell’energia, la simmetria spaziale la conservazione della quantità di moto, la simmetria angolare (la natura appare uguale da tutti gli angoli) la conservazione del momento angolare e così via. Questo è stato dimostrato da Emmy Noether semplicemente combinando le simmetrie con il principio di minima azione, una legge della natura che afferma che la natura tende a “prendere la via più breve”.
Trovo interessante quanto di tutta la complessità e l’apparente caos della natura possa essere spiegato da concetti intuitivi come “le leggi della natura non cambiano di giorno in giorno” e “la natura tende a prendere la via più breve”.
Torna ai campi
Fine dell’intermezzo, dove eravamo? Giusto, stavamo parlando di x³-3=0 e delle sue radici e campi.
Il campo di quell’equazione è Q(³√2, ζ) e sarebbe naturale pensare che sia così: a+b³√2+cζ, ma è sbagliato. La ragione è che vogliamo che il nostro campo sia “chiuso”. Cioè, se aggiungiamo o moltiplichiamo due elementi nel campo vogliamo che restino nel campo. Così per esempio ³√2 e ζ sono entrambi nel campo di cui sopra ma ³√2ζ non lo è.

Sottocampi e sottogruppi
Guardando i nostri esempi di grado 3 sopra abbiamo
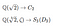
Sembrerebbe che il secondo campo e gruppo siano più complessi del primo campo e gruppo. Possiamo intuirlo contando semplicemente il numero di termini nel caso del campo o il numero di automorfismi nel caso del gruppo. Ma il solo contare non sembra catturare veramente ciò che significa essere complesso. Prendiamo per esempio il gruppo C₁₂. Un sacco di elementi, ma ruota solo le radici, quindi non sembra davvero così complesso. Un campo corrispondente è Q(e^π/6). Conterrà e^π/6,e^2π/6… ma di nuovo, non molto complesso.
Per capire quanto è complesso un gruppo sarà la chiave per capire perché alcune radici non possono essere descritte solo da radicali, ricordate.
Per apprezzare meglio la complessità introdurremo il concetto di “Sottocampo” e “Sottogruppo”. Un sottocampo è quando si rimuovono alcuni termini ma si ha ancora un campo chiuso. Allo stesso modo, un sottogruppo è quando si rimuovono alcuni degli automorfismi ma si ha ancora un gruppo chiuso.
Nel primo caso Q(√2), l’unica cosa che si può fare è rimuovere la √2 nel campo e uno dei due automorfismi nel gruppo (non possiamo rimuovere (e) e avere ancora un gruppo).
Per quanto riguarda il secondo caso Q(³√2, ζ), diventa un po’ più complicato. Si può distillare manualmente i sottocampi/gruppi semplicemente rimuovendo elementi uno alla volta e vedere se il campo/gruppo risultante è chiuso. Dopo un po’ si arriva a questo:
Interessante, sia il campo che il gruppo hanno quattro costituenti. Ora, sarebbe ragionevole pensare che i sottogruppi contengano sempre esattamente gli automorfismi dei sottocampi. Ma non è così.
Campi fissi
Non preoccupatevi, ci siamo quasi, è solo un po’ più complicato. Per vederlo, diamo un’occhiata al campo Q(⁴√2, i) e ai suoi sottocampi.
Il campo Q(⁴√2, i) ha il gruppo di permutazione D₄ (come un quadrato). Vediamo D₄ e i suoi sottogruppi.
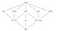
Il reticolo dei sottogruppi è capovolto in questa immagine con D₄ in basso, ci arriverò tra poco, ma guardiamo prima i sottocampi contro i sottogruppi. Q(⁴√2, i) ha 5 sottocampi grandi e 3 sottocampi piccoli, ma D₄ ha solo 3 sottogruppi grandi e 5 sottogruppi piccoli.
Sembrerebbe che non ci siano abbastanza gruppi grandi per permutare i 5 campi grandi. Se si dovesse giocare con i sottogruppi e i sottocampi si arriverebbe alla fine alla conclusione che i sottogruppi in realtà non permutano i sottocampi, ma piuttosto tutto ciò che non è nei sottocampi, che “fissano” o non toccano i sottocampi.
Così, per esempio, (f) fissa Q(⁴√2) e (r², f) fissa Q(√2).
Perché è così e non il contrario, come avevamo immaginato?
Non ho un modo intuitivo di spiegarlo, il modo in cui lo vedo è che lo abbiamo scoperto empiricamente e ora possiamo provare a provarlo. La dimostrazione va più o meno così:
Schizzo del teorema fondamentale della teoria di Galois
Vogliamo dimostrare che se capovolgiamo il reticolo dei sottogruppi otteniamo una corrispondenza uno-a-uno con il reticolo dei sottocampi dove i campi sono i campi fissi dei gruppi.
Prima, vorrei sottolineare che è ragionevole (più o meno) che sia così. Nel gruppo inferiore, abbiamo tutti gli automorfismi, che ovviamente si muovono intorno a tutto tranne Q (fissa Q), e in cima, abbiamo solo l’e-automorfismo, che non si muove intorno a niente (fissa tutto).
Se iniziamo dal gruppo inferiore e rimuoviamo alcuni degli automorfismi, gli automorfismi rimossi non si muoveranno più intorno a una piccola parte del campo e quindi fisseranno quella parte del campo. Man mano che rimuoviamo più automorfismi, una parte sempre più grande del campo sarà inalterata e quindi avremo un campo fisso più grande.
Per essere un po’ più rigorosi dovremo essere in grado di confrontare le dimensioni del gruppo e del campo. La dimensione del gruppo è, ovviamente, il numero di automorfismi in esso contenuti. La dimensione del campo è il numero di termini. Questi due sono uguali, ma perché è così?

Quotiente
Ora, potremmo guardare il reticolo di sottogruppi S₅ della quintica e vedere che effettivamente sembra piuttosto complesso. Ma per legare questo con i radicali abbiamo bisogno di un modo per analizzare la complessità tra i gruppi e i suoi sottogruppi. Cioè: Quanto è più complesso D₄ di C₄ per esempio? Per fare questo introduciamo il concetto di “Quoziente”. Un quoziente è fondamentalmente la divisione di gruppo. Come funziona?
Nella divisione ordinaria facciamo qualcosa del genere: Per dividere 15 mele su 5 persone, raggruppiamo le mele del gruppo di mele in 5 mucchi uguali e ogni mucchio corrisponderà a una persona del gruppo di persone. La risposta alla domanda 15/5 è 3, uno dei mucchi, qualsiasi mucchio va bene perché sono uguali.
Una cosa simile succede quando dividiamo i gruppi. Per dividere D₄ per C₄ raggruppiamo gli 8 elementi di D₄ in 4 gruppi uguali, uno per ogni elemento di C₄. Come facciamo a rendere i gruppi uguali? Non è che gli elementi siano tutti mele identiche. Possono essere automorfismi molto diversi, per esempio. Beh, i quozienti non sono sempre possibili proprio per questo motivo. Ma a volte un gruppo può essere diviso in “Coset”. Diciamo che dividiamo D₄ in 4 parti uguali con 2 elementi in ciascuna. Se siamo fortunati possiamo avere 4 pile di elementi in cui la relazione tra i due elementi è la stessa in tutte le pile. Per poterlo fare, il gruppo originale deve mostrare un alto livello di autosomiglianza. Per vedere questo, guardiamo un grafico di Cayley di D₄.
Come si può vedere c’è in effetti un alto livello di autosomiglianza. L’angolo superiore sinistro, superiore destro, inferiore sinistro e inferiore destro sono tutti uguali. Questo è il nostro coset.
Quindi D₄/C₄ è fondamentalmente uno di questi coset, che è C₂. Quindi: D₄/C₄=C₂.
Ora, introducendo i quozienti abbiamo effettivamente un concetto di come costruire gruppi da zero. Proprio come 21 consiste di 3 e 7, così i gruppi consistono dei loro sottogruppi. E proprio come possiamo ottenere i costituenti di un numero dividendo, 21/7=3, così possiamo ottenere i costituenti di un gruppo prendendo il quoziente. Poiché D₄/C₄=C₂, ciò significa che se abbiamo un gruppo C₄, dobbiamo moltiplicarlo per C₂ per arrivare a D₄. Poiché c’è una corrispondenza tra campi e gruppi, questo giocherà un ruolo nel modo in cui costruiamo i campi.
Radicali

Sottogruppi del quintico
Ora, Non mostrerò un’immagine del reticolo di gruppi di S₅ perché è troppo grande, ma dirò un paio di cose sui suoi sottogruppi. Uno dei sottogruppi è A₅ (gruppo alternato) che è facilmente verificabile. Per arrivare da A₅ a S₅ abbiamo bisogno di S₅/A₅=C₂. Quindi, possiamo arrivarci con i radicali, ma: Un sottogruppo di A₅ è (e), ma A₅/e non è un gruppo ciclico. Questo è vero per qualsiasi An con n≥5. Quindi non possiamo arrivarci per via radicale e, ahimè, qualsiasi polinomio di grado≥5 non può essere risolto per via radicale.
E fu così che Galois, da adolescente, inventò il concetto di gruppo per dimostrare una lunga questione aperta sull’irrisolvibilità del chinittico⁹.
Trisecting the angle
Un fatto bonus divertente che otteniamo dal macchinario che circonda la teoria di Galois, in questo caso la legge della torre per i campi, è una bella prova di un problema che ha sconcertato l’umanità fin dagli antichi greci, cioè: L’impossibilità di trisecare un angolo con una riga e un compasso. Apparentemente i greci amavano disegnare le cose in questo modo ed erano curiosi di conoscere i limiti del metodo.
Un esempio è trovare un punto in mezzo ad altri due punti. Per fare questo, mettete il compasso sui due punti e disegnate prima un cerchio intorno a uno e poi intorno all’altro. Usa la riga come righello e traccia una linea tra i punti e poi tra i punti in cui i cerchi si incrociano. Il centro è dove le linee si incrociano.
Ma come si traduce questo modo di disegnare nella teoria dei campi? Bene, si può vedere il problema di cui sopra come, diciamo che abbiamo un campo di due punti, (x₁,y₁) e (x₂,y₂). Vorremmo estendere il campo per contenere anche il punto centrale. Per fare questo troviamo le intersezioni dei cerchi (x-x₁)²+(y-y₁)²=r e (x-x₂)²+(y-y₂)²=r. Otteniamo due nuovi punti (x₃, y₃) e (x₄,y₄). La linea tra loro è y=(y₄-y₃)/(x₄-x₃)x. La linea tra i primi due punti è y=(y₂-y₁)/(x₂-x₁)x. Risolvi per x per ottenere dove si incrociano.
Apparentemente, le costruzioni con riga e compasso equivalgono a risolvere equazioni di grado uno e due.
Ma a cosa equivale trisecare un angolo?
La formula del triplo angolo produce:

Ma poiché usare riga e compasso equivale a risolvere equazioni di uno e due gradi, l’unica estensione di campo possibile è 2 per un’operazione, e poi usando i nuovi punti possiamo arrivare a potenze di 2: 4,8,16 ecc. ma mai 3.
Anche se è impossibile trisecare l’angolo usando solo riga e compasso è possibile usando l’origami.
Risolvere la quintica generale
Si deve dire che, anche se la quintica generale non si può risolvere con i radicali, si può risolvere con la “funzione theta di Jacobi”.
- Teoria di Galois per principianti: Una prospettiva storica. Jörg Bewersdorff
- http://pi.math.cornell.edu/~kbro…
- Automorfismi di campo
- https://kconrad.math.uconn.edu/b…
- https://faculty.math.illinois.ed…
- Wolfram|Alpha: Rendere la conoscenza del mondo computabile
- https://www.wikiwand.com/en/Galois_theory
- https://www.wikiwand.com/en/%C3%89variste_Galois
- https://www.youtube.com/watch?v=8qkfW35AqrQ&list=PLwV-9DG53NDxU337smpTwm6sef4x-SCLv&index=36