Nel gelato i piccoli cristalli di ghiaccio rotondi sono importanti per una consistenza morbida e cremosa. In generale, si ritiene che più veloce è la velocità di congelamento, più piccola è la dimensione dei cristalli di ghiaccio. Tuttavia, per alcuni materiali alimentari c’è un limite superiore per la velocità di congelamento. Se il congelamento è troppo veloce, le sollecitazioni meccaniche vengono impartite al materiale alimentare e può verificarsi una frattura da congelamento. In alcuni casi il processo di congelamento è usato per strutturare materiali, come il tradizionale piatto giapponese kori-tofu, o le impalcature usate nell’ingegneria biologica dei tessuti. Alcuni anni fa WUR, insieme a TU Delft e Unilever, ha studiato l’uso della liofilizzazione per strutturare le verdure da minestra. Qui, la dimensione dei cristalli di ghiaccio determina la dimensione dello spazio dei pori dopo l’essiccazione e aiuta la reidratazione delle verdure quando vengono mescolate alla zuppa.
Relazione tra la dimensione dei cristalli di ghiaccio e la velocità di congelamento
Quindi, dal punto di vista della qualità degli alimenti congelati, è importante avere buone conoscenze sulla relazione tra la dimensione dei cristalli di ghiaccio e la velocità di congelamento. Tuttavia, esistono solo alcune relazioni empiriche tra la velocità di congelamento e la dimensione dei cristalli di ghiaccio. Inoltre, per gli alimenti fabbricati ci sono altri mezzi usati per controllare la dimensione dei cristalli di ghiaccio, come i criopettenti come gli zuccheri e le proteine antigelo. Questo indica che ci si può aspettare un’interazione tra la composizione del materiale alimentare, la velocità di congelamento e la dimensione dei cristalli di ghiaccio, ma nelle relazioni empiriche la dipendenza dalla composizione del cibo è assente. Pertanto, Food & Biobased Research ha avviato un progetto di ricerca mirato a una comprensione più teorica della relazione tra tasso di congelamento, composizione e dimensione dei cristalli di ghiaccio utilizzando simulazioni al computer avanzate.
Modello di campo di fase per la crescita dei cristalli di ghiaccio
Per ottenere questo dettaglio di comprensione dobbiamo immergerci nella gamma micrometrica della microstruttura alimentare, dove i singoli cristalli di ghiaccio sono risolti nel modello al computer sviluppato, dove la crescita dei cristalli è modellata in funzione della composizione della matrice. Il metodo più avanzato in questo campo è il modello del campo di fase, che abbiamo utilizzato per descrivere la strutturazione di dispersioni come schiume ed emulsioni, stabilizzate con emulsionanti. Nel metodo del campo di fase si possono modellare simultaneamente diversi elementi individuali delle dispersioni, come gocce di emulsione, bolle di schiuma e cristalli. Il metodo permette facilmente la rottura e la coalescenza di questi elementi dispersi.
La forza del metodo sta nel modo in cui tratta l’interfaccia tra fasi disperse e continue. Qui, il metodo segue la proposta di un famoso fisico olandese, vanderWaals, di includere l’interfaccia in un quadro termodinamico. Usando il metodo del campo di fase abbiamo costruito un modello informatico per la descrizione dei cristalli di ghiaccio in una soluzione di saccarosio, il cui comportamento può essere visto come rappresentativo del gelato3. In ricerche precedenti abbiamo già chiarito la termodinamica delle soluzioni acquose di saccarosio4, e anche la velocità di trasporto dell’acqua nella soluzione di zucchero attraverso la diffusione5. Così, per queste proprietà del materiale abbiamo a disposizione teorie predittive in funzione della concentrazione di saccarosio per tutto l’intervallo da 0 a 100%.
Tasso di congelamento, composizione e dimensione dei cristalli di ghiaccio
Dopo aver sviluppato il modello informatico, abbiamo eseguito diverse simulazioni al computer per studiare la relazione tra tasso di congelamento, composizione e dimensione dei cristalli di ghiaccio. Abbiamo ingrandito una piccola parte del materiale alimentare e abbiamo seminato diversi nuclei per la crescita di cristalli di ghiaccio. Questa parte di materiale alimentare è stata poi sottoposta a una serie di velocità di congelamento. Le simulazioni sono state eseguite per due diverse concentrazioni di saccarosio – e una moltitudine di diverse posizioni casuali dei nuclei – al fine di ottenere delle buone statistiche.
Immagini di queste simulazioni al computer sono mostrate nella Figura 1. Gli elementi dispersi blu scuro sono singoli cristalli di ghiaccio. Il tasso di congelamento non è molto veloce, quindi possiamo assumere che i cristalli di ghiaccio rimangono approssimativamente sferici. Per comprendere i risultati della simulazione è importante sapere che i cristalli di ghiaccio non contengono zucchero, quindi la crescita dei cristalli di ghiaccio implica l’aumento della concentrazione di zucchero nella fase non congelata. L’aumento della concentrazione di zucchero porta ad un aumento del punto di congelamento, lasciando la matrice continua non congelata.

Figura 1: Istantanee della crescita dei cristalli di ghiaccio in una soluzione di zucchero ottenute tramite simulazioni al computer per diversi tassi di congelamento (0,01, 0,03 e 0,10 K/s dall’alto in basso) osservati in tempi diversi (da sinistra a destra). Osservare la coalescenza di diversi cristalli di ghiaccio, specialmente al basso tasso di congelamento (in alto)
Su un ulteriore congelamento i cristalli di ghiaccio possono impattare l’uno sull’altro, provocando un aumento della concentrazione di zucchero nel liquido non congelato in mezzo a loro, portando alla depressione del punto di congelamento. Quindi, si sviluppa un’interfaccia piatta. Se la velocità di congelamento è troppo lenta, gli zuccheri hanno il tempo di diffondersi fuori dalla zona di impingement e i cristalli possono coalizzarsi. Nella fase iniziale del congelamento, dove l’aumento locale della concentrazione di zucchero dovuto alla crescita dei cristalli di ghiaccio è piccolo, ci sono diversi eventi di coalescenza. Nella fase successiva del congelamento, la matrice non congelata si avvicina allo stato vetroso – dove la diffusione dell’acqua e dello zucchero si ferma e la crescita dei cristalli di ghiaccio si ferma.
Dalle simulazioni abbiamo determinato la dimensione media dei cristalli di ghiaccio e l’abbiamo tracciata contro la velocità di congelamento imposta per due diverse concentrazioni di saccarosio. Questi risultati sono mostrati nella figura 2.
Si può osservare una notevole dispersione nei dati di simulazione, a causa della stocastica del processo di nucleazione. Tuttavia, eseguendo molte simulazioni, si può adattare una relazione affidabile di legge di potenza attraverso i dati, che sono visualizzati come le linee che corrono attraverso i punti dei dati nella Figura 2 (pagina 00). L’adattamento mostra che gli esponenti della legge di potenza sono 0,31 e 0,18 per il 10% e il 15% di concentrazione iniziale di zucchero, rispettivamente. La nostra precedente relazione empirica ha un esponente della legge di potenza di 0,25, che è stato assunto essere indipendente dalla composizione. Il fatto che il valore empirico sia abbastanza vicino agli esponenti che abbiamo trovato tramite simulazione è molto incoraggiante. Inoltre, vale la pena notare che il modello di simulazione non ha richiesto alcun adattamento di parametri, poiché tutte le proprietà materiali e termodinamiche sono note.
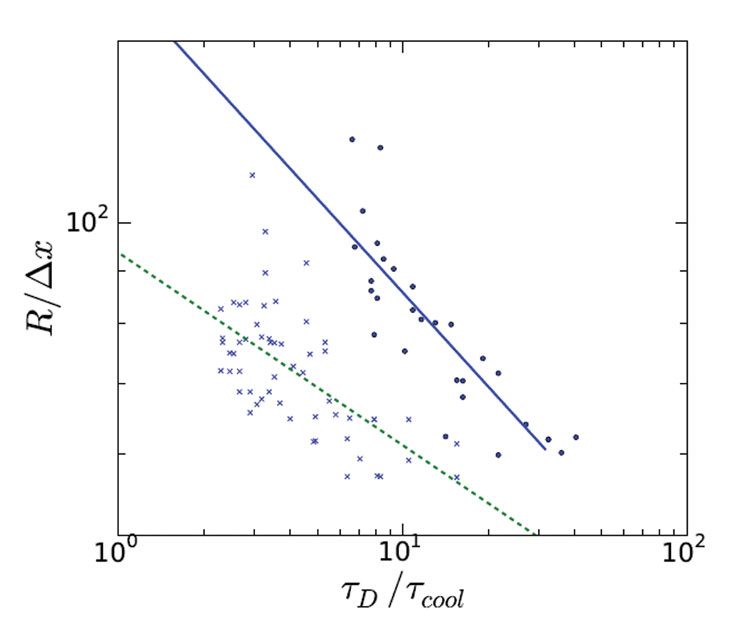
Figura 2: Dimensione media dei cristalli di ghiaccio rispetto al tasso di congelamento, per due diverse concentrazioni iniziali di zucchero (10% e 15%, indicate dalle linee solide e tratteggiate). Il raggio è misurato in unità della maglia di calcolo, che è di circa 3 micron, e il tasso di congelamento 1/tcool è misurato in termini di tasso di diffusione dell’acqua 1/tD. (a 0,01K/s se tD/tcool=1) I punti indicano la dimensione media di una singola simulazione. Le linee rappresentano relazioni di legge di potenza, adattate ai dati della simulazione
Problemi di qualità alimentare per frutta e verdura congelata
Food & La ricerca biobased conclude che il modello ha un grande grado di realismo. Inoltre, teorie predittive simili sulle proprietà materiali e termodinamiche sono disponibili per molti altri materiali alimentari. Di conseguenza il modello è, in linea di principio, applicabile a una moltitudine di altri materiali alimentari. Su questa base abbiamo lanciato un nuovo progetto di ricerca che continua a sviluppare e adattare il modello ai materiali alimentari congelati con una struttura cellulare per studiare i problemi di qualità degli alimenti congelati per frutta e verdura. Il modello del campo di fase sarà incorporato in un modello multiscala – perché nei prodotti alimentari sorgeranno differenze locali nel tasso di congelamento – che deve essere risolto con un approccio avanzato, dove il profilo di temperatura è calcolato alla scala del prodotto, e la crescita dei cristalli di ghiaccio alla microscala. Il modello informatico su macroscala chiamerà il modello su microscala più volte per una moltitudine di luoghi. Il modello su microscala riporterà la frazione di ghiaccio locale, mentre il modello su macroscala emetterà il gradiente di temperatura applicato al modello su microscala.
In questo nuovo progetto, Food & Biobased Research, non ci concentreremo solo sulla fase iniziale di congelamento, ma anche sulla conservazione congelata. Durante la conservazione le fluttuazioni di temperatura possono verificarsi a causa del raffreddamento meccanico o dell’apertura e chiusura della porta. Si presume che queste fluttuazioni di temperatura permettano ai cristalli di ghiaccio di crescere ulteriormente, il che è svantaggioso per la qualità del prodotto6. Vogliamo indagare se l’abbassamento della temperatura di conservazione rende il cibo meno sensibile alle fluttuazioni di temperatura, e anche se è possibile ottenere una riduzione del consumo energetico. Inoltre, anche quando la temperatura di conservazione è ragionevolmente costante, c’è ancora l’ispessimento della distribuzione dei cristalli di ghiaccio che si verifica durante la conservazione alle condizioni convenzionali di -18oC. Questo è dimostrato dal confronto tra il cibo congelato tramite congelamento ad aria e il congelamento a spostamento di pressione (PSF). Inizialmente, la dimensione dei cristalli di ghiaccio ottenuta tramite PSF è molto più piccola di quella ottenuta tramite congelamento ad aria convenzionale. Tuttavia, dopo diverse settimane di stoccaggio si riscontra una piccola differenza nella distribuzione finale delle dimensioni dei cristalli di ghiaccio, indicando che l’ingrossamento è avvenuto durante lo stoccaggio degli alimenti PSF7.
In sintesi, il nuovo modello di simulazione è uno strumento essenziale per immergersi nei possibili mezzi per l’industria dei surgelati per controllare la consistenza degli alimenti surgelati e le dimensioni dei cristalli di ghiaccio, in aree come 1) la formulazione del prodotto, 2) le condizioni di lavorazione e il tasso di congelamento. Conoscendo l’impatto della formulazione e della lavorazione sulla qualità dei surgelati, è possibile valutare nuove strategie per la conservazione dei surgelati per il loro impatto sia sulla qualità del prodotto che sul risparmio energetico.
- Voda, A., Homan, N., Witek, M., Duijster, A., van Dalen, G., van der Sman, R., Nijsse, J, van Vliet, L. Van As, H. & van Duynhoven, J. (2012). L’impatto della liofilizzazione sulla microstruttura e le proprietà di reidratazione della carota. Food Research International, 49(2), 687-693
- van der Sman, R. G. M., Voda, A., van Dalen, G., & Duijster, A. (2013). Intervallo dei cristalli di ghiaccio negli alimenti congelati. Journal of Food Engineering, 116(2), 622-626
- van der Sman, R. G. M. (2016). Simulazioni del campo di fase della crescita dei cristalli di ghiaccio in soluzioni di zucchero. International Journal of Heat and Mass Transfer, 95, 153-161
- van der Sman, R. G. M., & Meinders, M. B. J. (2011). Previsione del diagramma di stato delle miscele amido-acqua utilizzando la teoria del volume libero di Flory-Huggins. Soft Matter, 7(2), 429-442
- van der Sman, R. G. M., & Meinders, M. B. J. (2013). Diffusività dell’umidità nei materiali alimentari. Chimica alimentare, 138(2), 1265-1274
- Regand, A & Goff HD. “Struttura e ricristallizzazione del ghiaccio in sistemi modello di gelato stabilizzato congelato”. Food Hydrocolloids1 (2003): 95-102
- Fernández PP, Otero L, Martino MM ,Molina-García AD, & Sanz PD “High-pressure shift freezing: recrystallization during storage” European Food Research and Technology 5 (2008): 1367-1377
Chi è l’autore
Ruud van der Sman ha un MSc in Fisica Applicata alla Delft University of Technology e un PhD in Ingegneria Agricola alla Wageningen University. Lavora come ricercatore senior presso la Food & Biobased Research, e professore assistente part-time presso la Food Process Engineering – entrambe parte del Wageningen UR (centro di ricerca universitario &). I suoi interessi di ricerca comprendono la fisica della materia molle dei materiali alimentari, la modellazione al computer della strutturazione degli alimenti su scala micrometrica e la modellazione della fisiologia. La sua esperienza nella carne comprende la termodinamica della capacità di trattenere l’acqua, il trasferimento di calore e massa e la fisiologia post-mortem. www.wageningenur.nl/en/fbr