#InsideRL
In un tipico problema di Reinforcement Learning (RL), c’è un discente e un decisore chiamato agente e l’ambiente circostante con cui interagisce è chiamato ambiente. L’ambiente, in cambio, fornisce ricompense e un nuovo stato basato sulle azioni dell’agente. Quindi, nell’apprendimento di rinforzo, non insegniamo a un agente come dovrebbe fare qualcosa, ma gli presentiamo dei premi, positivi o negativi, in base alle sue azioni. Quindi la nostra domanda principale per questo blog è come formuliamo matematicamente qualsiasi problema in RL. È qui che entra in gioco il Markov Decision Process(MDP).

Prima di rispondere alla nostra domanda principale, cioè Come formuliamo matematicamente i problemi di RL (usando MDP), dobbiamo sviluppare la nostra intuizione su :
- La relazione Agente-Ambiente
- Proprietà di Markov
- Processo di Markov e catene di Markov
- Markov Reward Process (MRP)
- Equazione di Bellman
- Markov Reward Process
Prendi il tuo caffè e non fermarti finché sei orgoglioso!🧐
La relazione Agente-Ambiente
Prima vediamo alcune definizioni formali :
Agente : Programmi software che prendono decisioni intelligenti e sono i discenti nella RL. Questi agenti interagiscono con l’ambiente tramite azioni e ricevono ricompense in base alle loro azioni.
Ambiente: è la dimostrazione del problema da risolvere.Ora, possiamo avere un ambiente del mondo reale o un ambiente simulato con cui il nostro agente interagirà.

Stato : Questo è la posizione degli agenti in uno specifico time-step nell’ambiente.Quindi, ogni volta che un agente esegue un’azione l’ambiente dà all’agente una ricompensa e un nuovo stato dove l’agente ha raggiunto eseguendo l’azione.
Tutto ciò che l’agente non può cambiare arbitrariamente è considerato parte dell’ambiente. In termini semplici, le azioni possono essere qualsiasi decisione che vogliamo che l’agente impari e lo stato può essere qualsiasi cosa che può essere utile nella scelta delle azioni. Non assumiamo che tutto nell’ambiente sia sconosciuto all’agente, per esempio, il calcolo della ricompensa è considerato parte dell’ambiente anche se l’agente conosce un po’ come viene calcolata la sua ricompensa in funzione delle sue azioni e degli stati in cui vengono prese. Questo perché le ricompense non possono essere cambiate arbitrariamente dall’agente. A volte, l’agente potrebbe essere pienamente consapevole del suo ambiente ma trova comunque difficile massimizzare la ricompensa, come se sapessimo come giocare al cubo di Rubik ma non riuscissimo a risolverlo. Quindi, possiamo tranquillamente dire che la relazione agente-ambiente rappresenta il limite del controllo dell’agente e non la sua conoscenza.
La proprietà di Markov
Transizione: Il passaggio da uno stato all’altro è chiamato transizione.
Probabilità di transizione: La probabilità che l’agente si sposti da uno stato all’altro è chiamata probabilità di transizione.
La proprietà di Markov afferma che :
“Il futuro è indipendente dal passato dato il presente”
Matematicamente possiamo esprimere questa dichiarazione come :
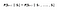
S indica lo stato attuale dell’agente e s indica lo stato successivo. Ciò che questa equazione significa è che la transizione dallo stato S a S è completamente indipendente dal passato. Quindi, l’RHS dell’equazione significa lo stesso dell’LHS se il sistema ha una proprietà di Markov. Intuitivamente significa che il nostro stato attuale cattura già l’informazione degli stati passati.
Probabilità di transizione di stato :
Come ora sappiamo sulla probabilità di transizione possiamo definire la probabilità di transizione di stato come segue :
Per lo stato di Markov da S a S cioè qualsiasi altro stato successore, la probabilità di transizione di stato è data da

Possiamo formulare la probabilità di transizione di stato in una matrice di probabilità di transizione di stato da :

Ogni riga della matrice rappresenta la probabilità di passare dal nostro stato originale o di partenza a qualsiasi stato successivo.La somma di ogni riga è uguale a 1.
Processo di Markov o Catene di Markov
Il processo di Markov è il processo casuale senza memoria, cioè una sequenza di uno stato casuale S,S,….S con una proprietà di Markov.La dinamica dell’ambiente può essere completamente definita usando gli stati (S) e la matrice di probabilità di transizione (P).
Ma cosa significa processo casuale?
Per rispondere a questa domanda guardiamo un esempio:
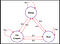
I bordi dell’albero indicano la probabilità di transizione. Da questa catena prendiamo qualche campione. Ora, supponiamo che stavamo dormendo e secondo la distribuzione di probabilità c’è una probabilità di 0,6 che corriamo e 0,2 che dormiamo di più e ancora 0,2 che mangiamo il gelato. Allo stesso modo, possiamo pensare ad altre sequenze che possiamo campionare da questa catena.
Alcuni campioni dalla catena :
- Sleep – Run – Ice-cream – Sleep
- Sleep – Ice-cream – Ice-cream – Run
Nelle due sequenze precedenti quello che vediamo è che otteniamo un insieme casuale di Stati(S) (cioè Sleep,Ice-cream,Sleep ) ogni volta che eseguiamo la catena.Spero che ora sia chiaro perché il processo di Markov è chiamato insieme casuale di sequenze.
Prima di andare al processo di Markov Reward diamo un’occhiata ad alcuni concetti importanti che ci aiuteranno a capire gli MRP.
Reward e Returns
Rewards sono i valori numerici che l’agente riceve eseguendo qualche azione in qualche stato(i) nell’ambiente. Il valore numerico può essere positivo o negativo in base alle azioni dell’agente.
Nell’apprendimento di rinforzo, ci preoccupiamo di massimizzare la ricompensa cumulativa (tutte le ricompense che l’agente riceve dall’ambiente) invece della ricompensa che l’agente riceve dallo stato corrente (chiamata anche ricompensa immediata). Questa somma totale della ricompensa che l’agente riceve dall’ambiente è chiamata rendimento.
Possiamo definire i ritorni come :
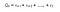
r è la ricompensa ricevuta dall’agente al passo temporale t mentre esegue un’azione(a) per passare da uno stato ad un altro. Allo stesso modo, r è la ricompensa ricevuta dall’agente al passo temporale t eseguendo un’azione per spostarsi in un altro stato. E, r è la ricompensa ricevuta dall’agente al passo temporale finale eseguendo un’azione per spostarsi in un altro stato.
Task episodici e continui
Task episodici: Questi sono i compiti che hanno uno stato terminale (stato finale) e possiamo dire che hanno stati finiti. Per esempio, nei giochi di corse, iniziamo il gioco (iniziare la corsa) e lo giochiamo fino alla fine del gioco (fine della corsa!). Questo è chiamato un episodio. Una volta che riavviamo il gioco, esso ripartirà da uno stato iniziale e quindi ogni episodio è indipendente.
Task continui: Questi sono i compiti che non hanno fine, cioè non hanno alcuno stato terminale. Questi tipi di compiti non finiranno mai. Per esempio, imparare a scrivere codice!
Ora, è facile calcolare i rendimenti dei compiti episodici perché alla fine finiranno, ma che dire dei compiti continui, che andranno avanti all’infinito. I rendimenti da sommare all’infinito! Quindi, come definiamo i rendimenti per i compiti continui?
Ecco dove abbiamo bisogno del Fattore di sconto (ɤ).
Fattore di sconto (ɤ): Determina quanta importanza deve essere data alla ricompensa immediata e alle ricompense future. In pratica ci aiuta ad evitare l’infinito come ricompensa nei compiti continui. Ha un valore tra 0 e 1. Un valore di 0 significa che si dà più importanza alla ricompensa immediata e un valore di 1 significa che si dà più importanza alle ricompense future. In pratica, un fattore di sconto di 0 non imparerà mai perché considera solo la ricompensa immediata e un fattore di sconto di 1 andrà avanti per le ricompense future che possono portare all’infinito. Pertanto, il valore ottimale per il fattore di sconto è compreso tra 0,2 e 0,8.
Quindi, possiamo definire i rendimenti usando il fattore di sconto come segue:(Diciamo che questa è l’equazione 1, poiché useremo questa equazione in seguito per derivare l’equazione di Bellman)

Comprendiamo con un esempio,supponiamo che viviate in un posto dove c’è scarsità d’acqua, quindi se qualcuno viene da voi e vi dice che vi darà 100 litri d’acqua!(supponiamo per favore!) per le prossime 15 ore in funzione di qualche parametro (ɤ).Vediamo due possibilità: (diciamo che questa è l’equazione 1, perché useremo questa equazione in seguito per derivare l’equazione di Bellman)
Una con fattore di sconto (ɤ) 0.8 :
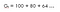
Questo significa che dovremmo aspettare fino alla 15a ora perché la diminuzione non è molto significativa, quindi vale ancora la pena di andare fino alla fine.Quindi, se il fattore di sconto è vicino a 1, allora faremo uno sforzo per andare fino alla fine perché le ricompense sono di importanza significativa.
Secondo, con fattore di sconto (ɤ) 0,2 :
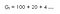
Questo significa che siamo più interessati alle ricompense anticipate in quanto le ricompense stanno diventando significativamente basse ad ogni ora.Quindi, potremmo non voler aspettare fino alla fine (fino alla 15° ora) in quanto non avrebbe valore.Quindi, se il fattore di sconto è vicino a zero allora le ricompense immediate sono più importanti di quelle future.
Quindi quale valore del fattore di sconto usare ?
Dipende dal compito per cui vogliamo allenare un agente. Supponiamo che in una partita a scacchi, l’obiettivo sia sconfiggere il re dell’avversario. Se diamo importanza alle ricompense immediate come una ricompensa sulla sconfitta del pedone di qualsiasi giocatore avversario, allora l’agente imparerà ad eseguire questi sotto-obiettivi non importa se anche i suoi giocatori vengono sconfitti. Quindi, in questo compito le ricompense future sono più importanti. In alcuni casi, potremmo preferire usare ricompense immediate come l’esempio dell’acqua che abbiamo visto prima.
Processo di Markov Reward
Fino ad ora abbiamo visto come la catena di Markov ha definito la dinamica di un ambiente usando un insieme di stati (S) e una matrice di probabilità di transizione (P).Ma, sappiamo che l’apprendimento per rinforzo è tutto sull’obiettivo di massimizzare la ricompensa.Quindi, aggiungiamo la ricompensa alla nostra catena di Markov.Questo ci dà il processo di Markov Reward.
Markov Reward Process: Come suggerisce il nome, gli MDP sono le catene di Markov con un giudizio sui valori.Fondamentalmente, otteniamo un valore da ogni stato in cui si trova il nostro agente.
Matematicamente, definiamo Markov Reward Process come :
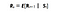
Cosa significa questa equazione è quanta ricompensa (Rs) otteniamo da un particolare stato S. Questo ci dice la ricompensa immediata da quel particolare stato in cui si trova il nostro agente. Come vedremo nella prossima storia come massimizzare queste ricompense da ogni stato in cui si trova il nostro agente. In termini semplici, massimizzando la ricompensa cumulativa che otteniamo da ogni stato.
Definiamo MRP come (S,P,R,ɤ), dove :
- S è un insieme di stati,
- P è la matrice di probabilità di transizione,
- R è la funzione di ricompensa, che abbiamo visto prima,
- ɤ è il fattore di sconto
Processo decisionale di Markov
Ora, sviluppiamo la nostra intuizione per l’equazione di Bellman e il processo decisionale di Markov.
Funzione di politica e funzione di valore
La funzione di valore determina quanto è buono per l’agente essere in un particolare stato. Naturalmente, per determinare quanto sarà buono essere in un particolare stato deve dipendere da alcune azioni che farà. È qui che entra in gioco la politica. Una politica definisce quali azioni eseguire in un particolare stato s.

Una politica è una funzione semplice, che definisce una distribuzione di probabilità sulle azioni (a∈ A) per ogni stato (s ∈ S). Se un agente al tempo t segue una politica π allora π(a|s) è la probabilità che l’agente con intraprenda un’azione (a ) in un particolare passo temporale (t).Nel Reinforcement Learning l’esperienza dell’agente determina il cambiamento della politica. Matematicamente, una politica è definita come segue:
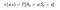
Ora, come troviamo il valore di uno stato.Il valore dello stato s, quando l’agente sta seguendo una politica π che è denotata da vπ(s) è il rendimento atteso partendo da s e seguendo una politica π per gli stati successivi, fino a raggiungere lo stato terminale.Possiamo formulare questo come :(Questa funzione è anche chiamata Funzione Stato-Valore)

Questa equazione ci dà il rendimento atteso partendo dallo stato(s) e andando agli stati successivi, con la politica π. Una cosa da notare è che i rendimenti che otteniamo sono stocastici mentre il valore di uno stato non è stocastico. È l’aspettativa dei rendimenti dallo stato iniziale s e, successivamente, a qualsiasi altro stato. E si noti anche che il valore dello stato terminale (se c’è) è zero. Vediamo un esempio :
Supponiamo che il nostro stato iniziale sia la classe 2, e passiamo alla classe 3 poi Pass e poi Sleep.In breve, classe 2 > classe 3 > Pass > Sleep.
Il nostro rendimento atteso è con fattore di sconto 0,5:
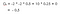
Nota:È -2 + (-2 * 0.5) + 10 * 0.25 + 0 invece di -2 * -2 * 0.5 + 10 * 0.25 + 0.Allora il valore della classe 2 è -0.5 .
Equazione di Bellman per la funzione di valore
L’equazione di Bellman ci aiuta a trovare le politiche ottimali e la funzione di valore. Sappiamo che la nostra politica cambia con l’esperienza, quindi avremo diverse funzioni di valore secondo le diverse politiche.
L’equazione di Bellman afferma che la funzione di valore può essere decomposta in due parti:
- Ricompensa immediata, R
- Valore attualizzato degli stati successivi,
Matematicamente, possiamo definire l’equazione di Bellman come :

Comprendiamo cosa dice questa equazione con l’aiuto di un esempio :
Supponiamo che ci sia un robot in qualche stato (s) e poi si muova da questo stato a qualche altro stato (s’). Ora, la domanda è quanto bene ha fatto il robot a trovarsi nello stato (s). Usando l’equazione di Bellman, possiamo dire che è l’aspettativa di ricompensa che ha ottenuto lasciando lo stato (s) più il valore dello stato (s’) in cui si è spostato.
Guardiamo un altro esempio :
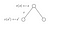
Vogliamo conoscere il valore dello stato s.Il valore dello stato s è la ricompensa che abbiamo ottenuto lasciando quello stato, più il valore scontato dello stato su cui siamo atterrati moltiplicato per la probabilità di transizione in cui ci muoveremo.
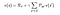
L’equazione precedente può essere espressa in forma di matrice come segue:

Dove v è il valore dello stato in cui ci trovavamo, che è uguale alla ricompensa immediata più il valore scontato dello stato successivo moltiplicato per la probabilità di muoversi in quello stato.
La complessità del tempo di esecuzione per questo calcolo è O(n³). Pertanto, questa non è chiaramente una soluzione pratica per la risoluzione di grandi MRP (lo stesso vale per gli MDP). Nei prossimi blog, vedremo metodi più efficienti come la programmazione dinamica (iterazione del valore e iterazione della politica), metodi Monte-Claro e TD-Learning.
Parleremo dell’equazione di Bellman in modo molto più dettagliato nella prossima storia.
Che cos’è il processo decisionale di Markov?
Processo decisionale di Markov: è un processo di ricompensa di Markov con una decisione.Tutto è uguale a MRP ma ora abbiamo un’agenzia reale che prende decisioni o intraprende azioni.
È una tupla di (S, A, P, R, 𝛾) dove:
- S è un insieme di stati,
- A è l’insieme delle azioni che l’agente può scegliere di intraprendere,
- P è la matrice delle probabilità di transizione,
- R è la ricompensa accumulata dalle azioni dell’agente,
- 𝛾 è il fattore di sconto.
P e R cambieranno leggermente con le azioni come segue:
Matrice di probabilità di transizione
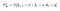
Funzione di ricompensa
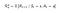
Ora, la nostra funzione di ricompensa dipende dall’azione.
Finora abbiamo parlato di ottenere una ricompensa (r) quando il nostro agente passa attraverso un insieme di stati (s) seguendo una politica π.In realtà, in un processo decisionale di Markov (MDP) la politica è il meccanismo per prendere decisioni, quindi ora abbiamo un meccanismo che sceglierà di intraprendere un’azione.
Le politiche in un MDP dipendono dallo stato corrente, non dipendono dalla storia, questa è la proprietà di Markov, quindi lo stato corrente caratterizza la storia.
Abbiamo già visto quanto è buono per l’agente essere in un particolare stato (funzione stato-valore).Ora, vediamo quanto è buono prendere una particolare azione seguendo una politica π dallo stato s (funzione azione-valore).
Funzione stato-azione valore o funzione Q
Questa funzione specifica quanto è buono per l’agente prendere un’azione (a) in uno stato (s) con una politica π.
Matematicamente, possiamo definire la funzione di valore stato-azione come :

In pratica, ci dice il valore di eseguire una certa azione (a) in uno stato (s) con una politica π.
Guardiamo un esempio di Processo Decisionale di Markov :
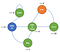
Ora, possiamo vedere che non ci sono più probabilità.Infatti ora il nostro agente ha delle scelte da fare come dopo il risveglio, possiamo scegliere di guardare netflix o di codificare e fare il debug, naturalmente le azioni dell’agente sono definite in base a qualche politica π e riceveranno la ricompensa di conseguenza.
.