Nel tutorial sui modelli lineari generalizzati, abbiamo imparato a conoscere vari GLM come la regressione lineare, la regressione logistica, ecc. In questo tutorial della serie TechVidvan’s R tutorial, ci occuperemo della regressione lineare in R in dettaglio. Impareremo cos’è la regressione lineare in R e come implementarla in R. Guarderemo il metodo di stima dei minimi quadrati e impareremo anche come controllare l’accuratezza del modello.

Quindi, senza ulteriori indugi, cominciamo!

Regressione lineare in R

La regressione lineare in R è un metodo usato per prevedere il valore di una variabile usando il valore (o i valori) di una o più variabili predittive di input. L’obiettivo della regressione lineare è di stabilire una relazione lineare tra la variabile di uscita desiderata e i predittori di ingresso.

Modellare una variabile continua Y come funzione di una o più variabili predittrici di ingresso Xi, in modo che la funzione possa essere usata per prevedere il valore di Y quando sono noti solo i valori di Xi. La forma generale di tale relazione lineare è:

Y=?0+?1 X

Qui, ?0 è l’intercetta
e ?1 è la pendenza.

Tipi di regressione lineare in R

Ci sono due tipi di regressione lineare in R:

• Regressione lineare semplice
• Regressione lineare multipla

Vediamoli uno per uno.

Regressione lineare semplice in R

La regressione lineare semplice mira a trovare una relazione lineare tra due variabili continue. È importante notare che la relazione è di natura statistica e non deterministica.

Una relazione deterministica è quella in cui il valore di una variabile può essere trovato accuratamente usando il valore dell’altra variabile. Un esempio di relazione deterministica è quella tra chilometri e miglia. Usando il valore del chilometro, possiamo trovare accuratamente la distanza in miglia. Una relazione statistica non è accurata e ha sempre un errore di previsione. Per esempio, dati abbastanza dati, possiamo trovare una relazione tra l’altezza e il peso di una persona, ma ci sarà sempre un margine di errore e ci saranno casi eccezionali.

L’idea dietro la semplice regressione lineare è di trovare una linea che si adatti meglio ai valori dati di entrambe le variabili. Questa linea può poi aiutarci a trovare i valori della variabile dipendente quando sono mancanti.

Studiamo questo con l’aiuto di un esempio. Abbiamo un set di dati composto dalle altezze e dai pesi di 500 persone. Il nostro obiettivo è quello di costruire un modello di regressione lineare che formuli la relazione tra altezza e peso, in modo tale che quando diamo l’altezza (Y) come input al modello, esso possa darci in cambio il peso (X) con il minimo margine o errore.

Y=b0+b1X

I valori di b0 e b1 dovrebbero essere scelti in modo da minimizzare il margine di errore. La metrica dell’errore può essere usata per misurare l’accuratezza del modello.

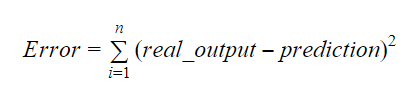
Possiamo calcolare la pendenza o il coefficiente come: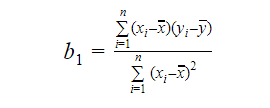

Il valore di b1 ci dà un’idea della natura della relazione tra le variabili dipendenti e indipendenti.

• Se b1 > 0, allora le variabili hanno una relazione positiva, cioè un aumento di x provocherà un aumento di y.
• Se b1 < 0, allora le variabili hanno una relazione negativa, cioè un aumento di x provocherà una diminuzione di y.

Il valore di b0 o intercetta può essere calcolato come segue: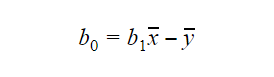
Il valore di b0 può anche dare molte informazioni sul modello e viceversa.

Se il modello non include x=0, allora la predizione non ha senso senza b1. Perché il modello abbia solo b0 e non b1 in qualsiasi punto, il valore di x deve essere 0 in quel punto. In casi come l’altezza, x non può essere 0 e l’altezza di una persona non può essere 0. Pertanto, tale modello è privo di significato con solo b0.

Se il termine b0 manca, allora il modello passerà attraverso l’origine, il che significa che la predizione e il coefficiente di regressione (pendenza) saranno distorti.

Regressione lineare multipla in R

La regressione lineare multipla è un’estensione della regressione lineare semplice. Nella regressione lineare multipla, miriamo a creare un modello lineare che possa prevedere il valore della variabile obiettivo usando i valori di più variabili predittive. La forma generale di tale funzione è la seguente:

Y=b0+b1X1+b2X2+…+bnXn

Valutazione della precisione del modello

Ci sono vari metodi per valutare la qualità e la precisione del modello. Diamo un’occhiata ad alcuni di questi metodi uno alla volta.

R-Squared

La vera informazione nei dati è la varianza trasportata in essi. L’R-squared ci dice la proporzione di variazione nella variabile obiettivo (y) spiegata dal modello. Possiamo trovare la misura R-squared di un modello usando la seguente formula: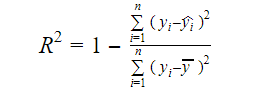

dove,

• yi è il valore montato di y per l’osservazione i
• y è la media di Y.

Un valore inferiore di R-squared indica una minore accuratezza del modello. Tuttavia, la misura di R-squared non è necessariamente un fattore decisivo finale.

Adjusted R-Squared

Quando il numero di variabili aumenta nel modello, anche il valore di R-squared aumenta. Questo causa anche errori nella variazione spiegata dalle nuove variabili aggiunte. Pertanto, aggiustiamo la formula per l’R quadrato per variabili multiple.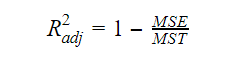
Qui, il MSE sta per Errore Standard Medio che è:

E MST sta per Totale Standard Medio che è dato da: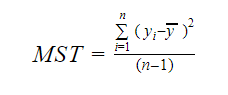

dove, n è il numero delle osservazioni e q è il numero dei coefficienti.

La relazione tra R-squared e R-squared aggiustato è: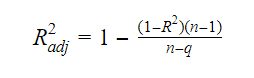

Standard Error e F-Statistic

L’errore standard e la F-statistic sono entrambe misure della qualità dell’adattamento di un modello. Le formule per l’errore standard e la statistica F sono:

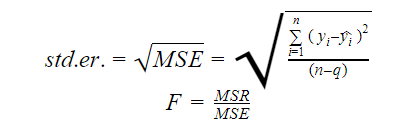
Dove MSR sta per Mean Square Regression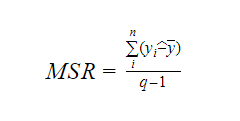

AIC e BIC

Il criterio di informazione di Akaike e il criterio di informazione bayesiano sono misure della qualità dell’adattamento dei modelli statistici. Possono anche essere usati come criteri per la selezione di un modello.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

dove,

• L è la funzione di likelihood,
• k è il numero di parametri del modello,
• n è la dimensione del campione.

Funzione lm in R

La funzione lm() di R adatta modelli lineari. Può effettuare la regressione, l’analisi della varianza e della covarianza. La sintassi della funzione lm è la seguente:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

dove,

• formula è un oggetto di classe “formula” ed è una rappresentazione simbolica del modello da adattare,
• dati è il data frame o la lista che contiene le variabili nella formula (data è un argomento opzionale. Se manca, la funzione prende le variabili dall’ambiente),
• subset è un vettore opzionale contenente un sottoinsieme di osservazioni che devono essere utilizzate nel processo di adattamento,
• weights è un vettore opzionale che specifica i pesi da utilizzare nel processo di adattamento,
• na.action è una funzione che mostra cosa dovrebbe accadere quando si incontrano degli NA nei dati,
• method indica il metodo di adattamento del modello,
• model, x, y, e qr sono logiche che controllano se i valori corrispondenti devono essere restituiti con l’output o meno. Questi valori sono:
• model: la struttura del modello
• x: la matrice del modello
• y: la risposta
• qr: la decomposizione qr
• singular.ok è una logica che controlla se i fit singolari sono permessi o meno,
• offset è un predittore precedentemente noto che dovrebbe essere usato nel modello,
• . . sono argomenti aggiuntivi da passare alle funzioni di regressione di livello inferiore.

Esempio pratico di regressione lineare in R

Questa è abbastanza teoria per ora. Diamo un’occhiata a come implementare tutto questo. Adatteremo un modello lineare usando la regressione lineare in R con l’aiuto della funzione lm(). In seguito controlleremo anche la qualità dell’adattamento del modello. Usiamo il dataset auto che è fornito di default nel pacchetto base di R.

1. Iniziamo con un’analisi grafica del dataset per familiarizzare con esso. Per farlo disegneremo uno scatter plot e controlleremo cosa ci dice sui dati.

Possiamo usare la funzione scatter.smooth() per creare uno scatter plot per il dataset.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Output

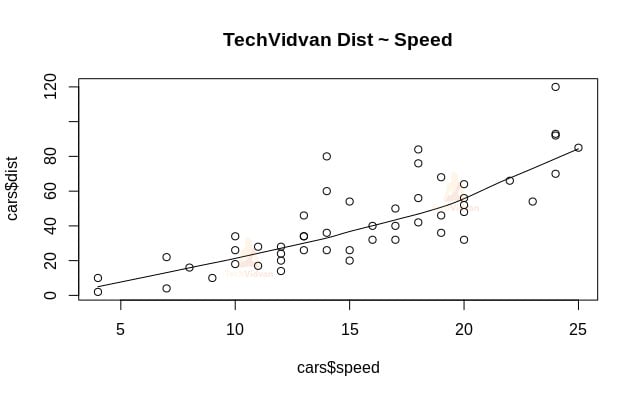
Lo scatter plot ci mostra una correlazione positiva tra distanza e velocità. Suggerisce una relazione linearmente crescente tra le due variabili. Questo rende i dati adatti alla regressione lineare, poiché una relazione lineare è un presupposto fondamentale per l’adattamento di un modello lineare sui dati.

2. Ora che abbiamo verificato che la regressione lineare è adatta ai dati, possiamo usare la funzione lm() per adattarvi un modello lineare.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Output

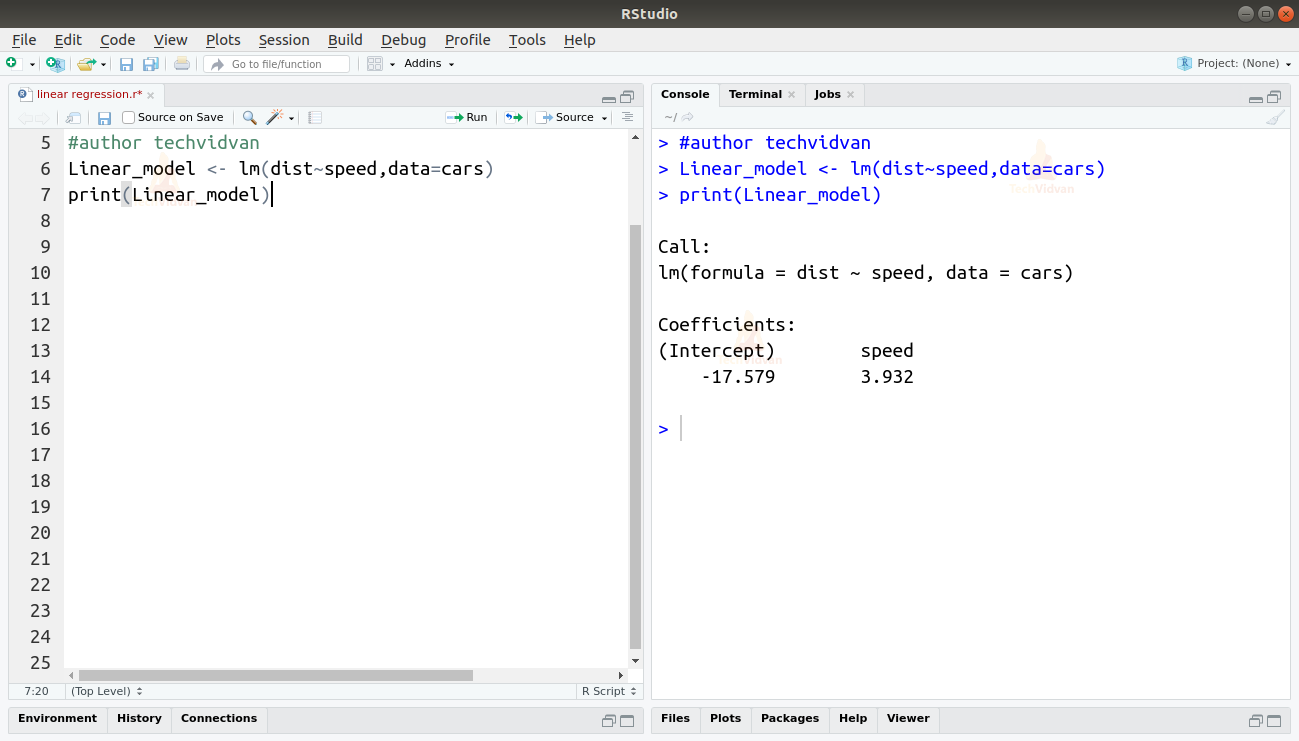
L’output della funzione lm() ci mostra l’intercetta e il coefficiente di velocità. Definendo così la relazione lineare tra distanza e velocità come:

Distanza=Intercetta+coefficiente*velocità

Distanza=-17.579+3.932*velocità

3. Ora che abbiamo montato un modello, controlliamo la qualità o bontà dell’adattamento. Cominciamo controllando il riassunto del modello lineare usando la funzione summary().

summary(Linear_model)

Output

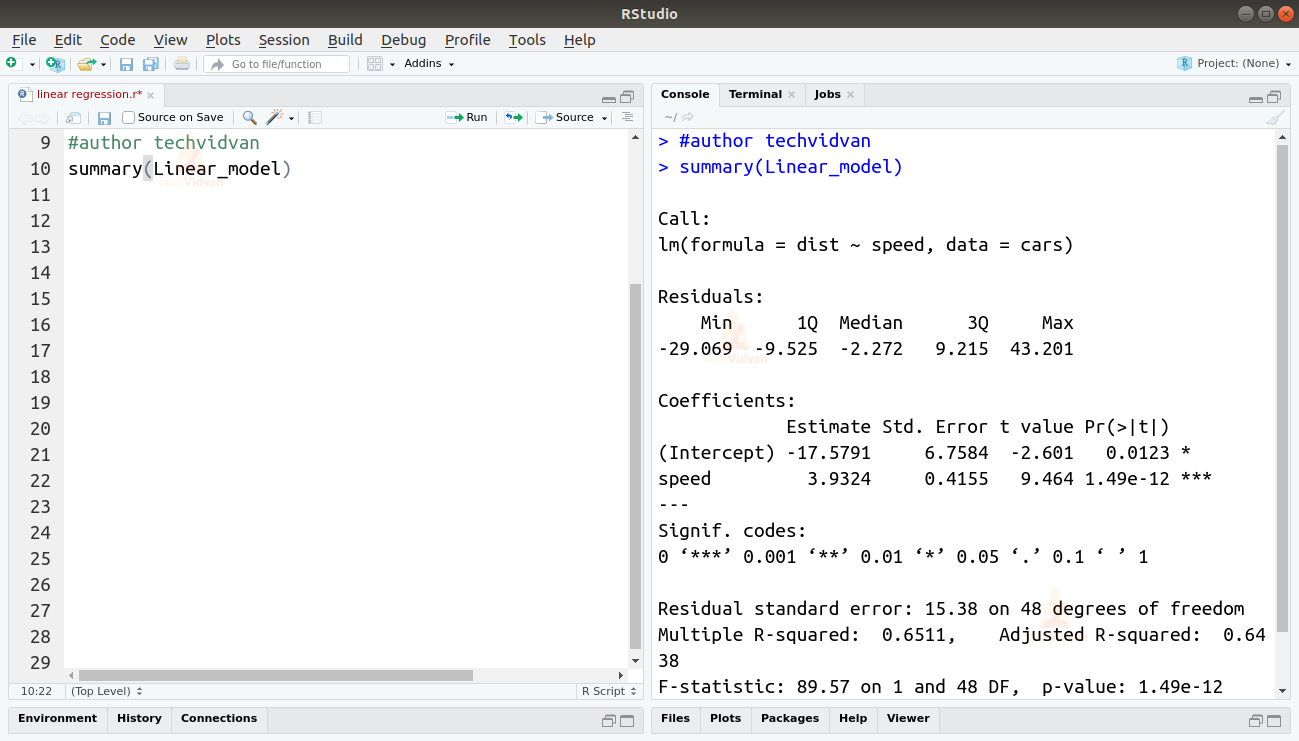
La funzione summary() ci dà alcune misure importanti per aiutarci a diagnosticare l’adattamento del modello. Il valore p è un’importante misura della bontà dell’adattamento di un modello. Si dice che un modello non è adatto se il valore p è più di un livello di significatività statistica predeterminato che idealmente è 0,05.

Il sommario ci fornisce anche il valore t. Più il valore t è alto, più il modello è adatto.
Possiamo anche trovare l’AIC e il BIC usando le funzioni AIC() e BIC().

AIC(Linear_model)BIC(Linear_model)

Output

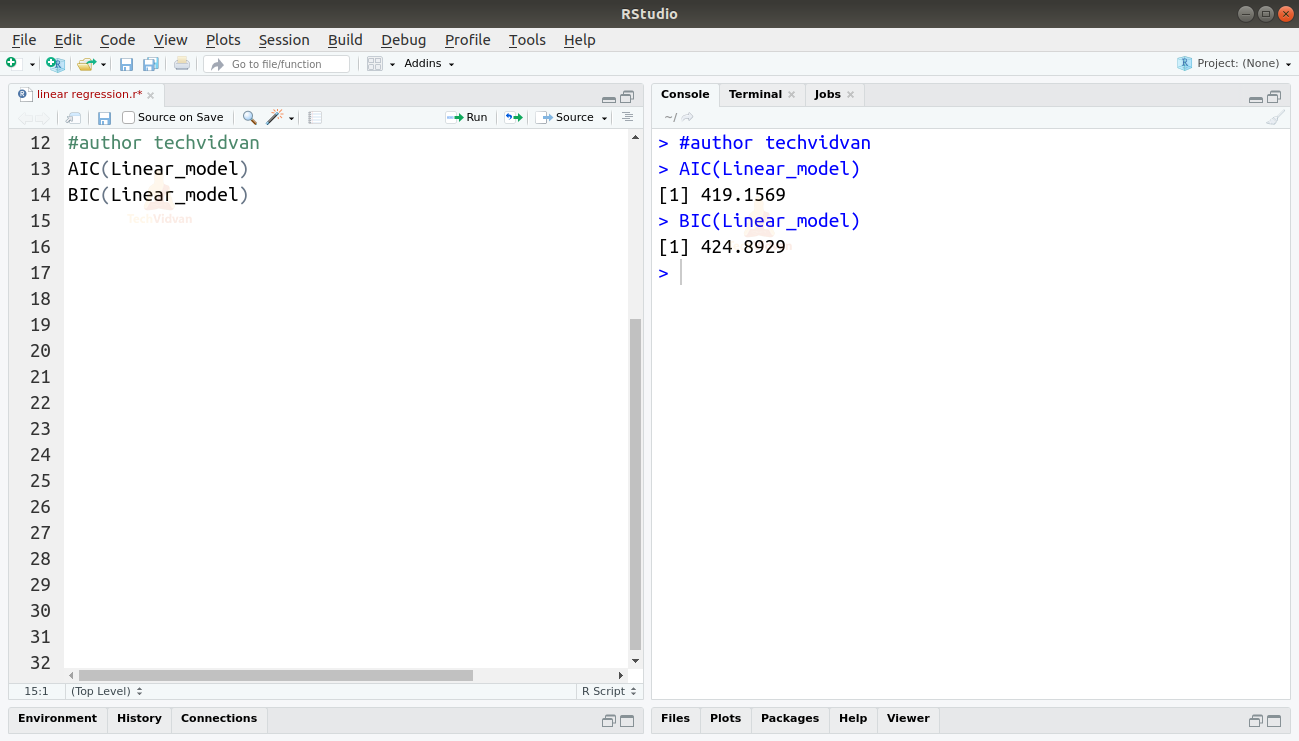
Il modello che risulta nel più basso punteggio AIC e BIC è il più preferito.

Sommario

In questo capitolo della serie di tutorial R di TechVidvan, abbiamo imparato la regressione lineare. Abbiamo imparato la regressione lineare semplice e la regressione lineare multipla. Poi abbiamo studiato varie misure per valutare la qualità o l’accuratezza del modello, come R2, R2 corretto, errore standard, F-statistica, AIC e BIC. Abbiamo poi imparato come implementare la regressione lineare in R. Abbiamo poi controllato la qualità dell’adattamento del modello in R.

Condividi la tua valutazione su Google se ti è piaciuto il tutorial sulla regressione lineare.