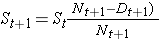Siamo spesso interessati a valutare se ci sono differenze nella sopravvivenza (o incidenza cumulativa di eventi) tra diversi gruppi di partecipanti. Per esempio, in uno studio clinico con un risultato di sopravvivenza, potremmo essere interessati a confrontare la sopravvivenza tra i partecipanti che ricevono un nuovo farmaco rispetto a un placebo (o una terapia standard). In uno studio osservazionale, potremmo essere interessati a confrontare la sopravvivenza tra uomini e donne, o tra partecipanti con e senza un particolare fattore di rischio (ad esempio, ipertensione o diabete). Ci sono diversi test disponibili per confrontare la sopravvivenza tra gruppi indipendenti.

Il Log Rank Test

Il log rank test è un test popolare per verificare l’ipotesi nulla di nessuna differenza nella sopravvivenza tra due o più gruppi indipendenti. Il test confronta l’intera esperienza di sopravvivenza tra i gruppi e può essere pensato come un test per verificare se le curve di sopravvivenza sono identiche (sovrapposte) o meno. Le curve di sopravvivenza sono stimate per ogni gruppo, considerato separatamente, usando il metodo Kaplan-Meier e confrontate statisticamente usando il log rank test. È importante notare che ci sono diverse varianti del log rank test statistico che sono implementate da vari pacchetti di calcolo statistico (ad esempio, SAS, R 4,6). Presentiamo qui una versione che è strettamente legata alla statistica del test del chi-quadrato e confronta il numero di eventi osservati con il numero di eventi attesi ad ogni punto temporale durante il periodo di follow-up.

Esempio:

Un piccolo studio clinico viene eseguito per confrontare due trattamenti combinati in pazienti con cancro gastrico avanzato. Venti partecipanti con cancro gastrico in stadio IV che acconsentono a partecipare allo studio sono assegnati in modo casuale a ricevere la chemioterapia prima dell’intervento o la chemioterapia dopo l’intervento. L’esito primario è la morte e i partecipanti sono seguiti fino a 48 mesi (4 anni) dopo l’arruolamento nello studio. Le esperienze dei partecipanti in ogni braccio dello studio sono riportate di seguito.

Chemotherapy Before Surgery			Chemotherapy After Surgery
Mese di Morte	Mese dell’ultimo contatto		Mese della morte	Mese dell’ultimo contatto
8	8		33	48
12	32		28	48
26	20		41	25
14	40			37
21				48
27				25
				43

Sei partecipanti nel gruppo chemioterapia prima dell’intervento chirurgico muoiono nel corso del follow-rispetto ai tre partecipanti del gruppo “chemioterapia dopo l’intervento”. Gli altri partecipanti di ciascun gruppo sono seguiti per un numero variabile di mesi, alcuni fino alla fine dello studio a 48 mesi (nel gruppo della chemioterapia dopo l’intervento). Usando le procedure descritte sopra, costruiamo prima le tabelle di vita per ogni gruppo di trattamento usando l’approccio Kaplan-Meier.

Tabella di vita per il gruppo che riceve la chemioterapia prima della chirurgia

Tempo, Mesi	Numero a rischio Nt	Numero di morti Dt	Numero censurato Ct	Probabilità di sopravvivenza
0	10			1
8	10	1	1	0.900
12	8	1		0.788
14	7	1		0.675
20	6		1	0.675
21	5	1		0.540
26	4	1		0.405
27	3	1		0.270
32	2		1	0.270
40	1		1	0.270

Tabella di vita per il gruppo che riceve la chemioterapia dopo la chirurgia

Tempo, Mesi	Numero a rischio Nt	Numero di morti Dt	Numero censurato Ct	Probabilità di sopravvivenza
0	10			1
25	10		2	1.000
28	8	1		0.875
33	7	1		0.750
37	6		1	0.750
41	5	1		0.600
43	4		1	0.600
48	3		3	0.600

Le due curve di sopravvivenza sono riportate di seguito.

Sopravvivenza in ogni gruppo di trattamento

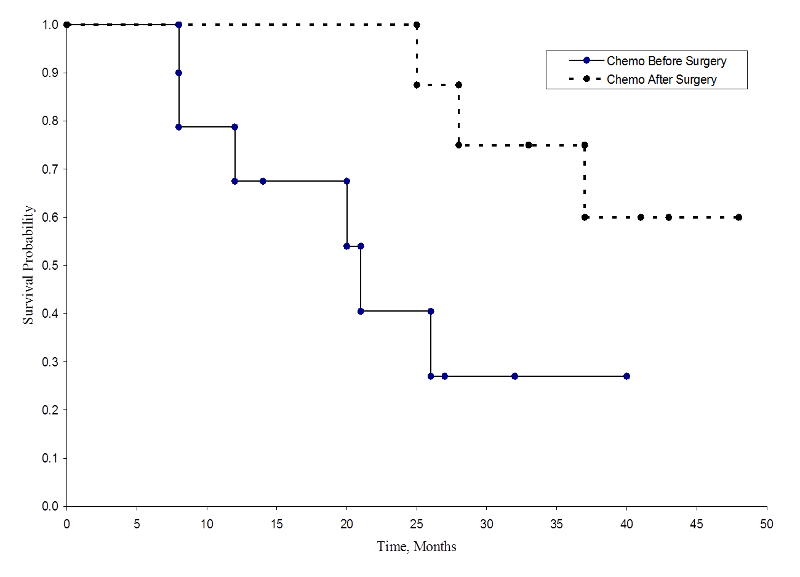
Le probabilità di sopravvivenza per il gruppo chemioterapia dopo la chirurgia sono più alte delle probabilità di sopravvivenza per il gruppo chemioterapia prima della chirurgia, suggerendo un beneficio di sopravvivenza. Tuttavia, queste curve di sopravvivenza sono stimate da piccoli campioni. Per confrontare la sopravvivenza tra i gruppi possiamo usare il test log rank. L’ipotesi nulla è che non c’è differenza di sopravvivenza tra i due gruppi o che non c’è differenza tra le popolazioni nella probabilità di morte in qualsiasi punto. Il log rank test è un test non parametrico e non fa ipotesi sulle distribuzioni di sopravvivenza. In sostanza, il log rank test confronta il numero di eventi osservati in ogni gruppo con quello che ci si aspetterebbe se l’ipotesi nulla fosse vera (cioè se le curve di sopravvivenza fossero identiche).

H0: Le due curve di sopravvivenza sono identiche (o S1t = S2t) contro H1: Le due curve di sopravvivenza non sono identiche (o S1t ≠ S2t, in qualsiasi momento t) (α=0,05).

La statistica log rank è approssimativamente distribuita come una statistica di test chi-quadro. Ci sono diverse forme della statistica di test, e variano in termini di come vengono calcolate. Noi usiamo la seguente:

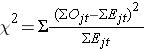
dove ΣOjt rappresenta la somma del numero osservato di eventi nel jesimo gruppo nel tempo (ad esempio, j=1,2) e ΣEjt rappresenta la somma del numero atteso di eventi nel jesimo gruppo nel tempo.

Le somme del numero osservato e atteso di eventi sono calcolate per ogni tempo di evento e sommate per ogni gruppo di confronto. La statistica log rank ha gradi di libertà pari a k-1, dove k rappresenta il numero di gruppi di confronto. In questo esempio, k=2 quindi la statistica di test ha 1 grado di libertà.

Per calcolare la statistica di test abbiamo bisogno del numero osservato e atteso di eventi per ogni tempo di evento. Il numero osservato di eventi proviene dal campione e il numero atteso di eventi è calcolato assumendo che l’ipotesi nulla sia vera (cioè che le curve di sopravvivenza siano identiche).

Per generare il numero atteso di eventi organizziamo i dati in una tabella di vita con righe che rappresentano ogni tempo di evento, indipendentemente dal gruppo in cui l’evento è avvenuto. Teniamo anche traccia dell’assegnazione del gruppo. Poi stimiamo la proporzione di eventi che si verificano in ogni momento (Ot/Nt) usando i dati di entrambi i gruppi combinati sotto l’ipotesi di nessuna differenza nella sopravvivenza (cioè, assumendo che l’ipotesi nulla sia vera). Moltiplichiamo queste stime per il numero di partecipanti a rischio in quel momento in ciascuno dei gruppi di confronto (N1t e N2t per i gruppi 1 e 2 rispettivamente).

Specificamente, calcoliamo per ogni evento al tempo t, il numero a rischio in ciascun gruppo, Njt (ad esempio, dove j indica il gruppo, j=1, 2) e il numero di eventi (morti), Ojt, in ciascun gruppo. La tabella seguente contiene le informazioni necessarie per condurre il test log rank per confrontare le curve di sopravvivenza di cui sopra. Il gruppo 1 rappresenta il gruppo della chemioterapia prima della chirurgia, e il gruppo 2 rappresenta il gruppo della chemioterapia dopo la chirurgia.

Dati per il log rank test per confrontare le curve di sopravvivenza

Tempo, Mesi	Numero a rischio nel Gruppo 1 N1t	Numero a rischio nel Gruppo 2 N2t	Numero di eventi (decessi) nel Gruppo 1 O1t	Numero di eventi (morti) nel gruppo 2 O2t
8	10	10	1	0
12	8	10	1	0
14	7	10	1	0
21	5	10	1	0
26	4	8	1	0
27	3	8	1	0
28	2	8	0	1
33	1	7	0	1
41	0	5	0	1

Poi sommiamo il numero a rischio, Nt = N1t+N2t, in ogni momento dell’evento e il numero di eventi osservati (morti), Ot = O1t+O2t, in ogni momento dell’evento. Poi calcoliamo il numero atteso di eventi in ogni gruppo. Il numero atteso di eventi è calcolato ad ogni tempo di evento come segue:

E1t = N1t*(Ot/Nt) per il gruppo 1 e E2t = N2t*(Ot/Nt) per il gruppo 2. I calcoli sono riportati nella tabella seguente.

Numero previsto di eventi in ogni gruppo

Tempo, Mesi	Numero a rischio nel Gruppo 1 N1t	Numero a rischio nel Gruppo 2 N2t	Numero totale a rischio Nt	Numero di eventi nel gruppo 1 O1t	Numero di eventi nel gruppo 2 O2t	Numero totale di eventi Ot	Numero previsto di eventi in Gruppo 1 E1t = N1t*(Ot/Nt)	Numero previsto di eventi in Gruppo 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000

Successivamente sommiamo i numeri di eventi osservati in ogni gruppo (∑O1t e ΣO2t) e i numeri di eventi previsti in ogni gruppo (ΣE1t e ΣE2t) nel tempo. Questi sono mostrati nella riga inferiore della tabella seguente.

Numero totale osservato e atteso di eventi in ogni gruppo

Tempo, Mesi	Numero a rischio nel Gruppo 1 N1t	Numero a rischio nel Gruppo 2 N2t	Numero totale a rischio Nt	Numero di eventi nel gruppo 1 O1t	Numero di eventi nel gruppo 2 O2t	Numero totale di eventi Ot	Numero previsto di eventi in Gruppo 1 E1t = N1t*(Ot/Nt)	Numero previsto di eventi in Gruppo 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000
				6	3		2.620	6.380

Possiamo ora calcolare la statistica del test:

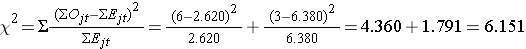
La statistica del test è approssimativamente distribuita come chi-quadrato con 1 grado di libertà. Così, il valore critico per il test può essere trovato nella tabella dei valori critici della distribuzione Χ2.

Per questo test la regola di decisione è di rifiutare H0 se Χ2 > 3,84. Osserviamo Χ2 = 6,151, che supera il valore critico di 3,84. Pertanto, rifiutiamo H0. Abbiamo prove significative, α=0,05, per dimostrare che le due curve di sopravvivenza sono diverse.

Esempio:

Un ricercatore desidera valutare l’efficacia di un breve intervento per prevenire il consumo di alcol in gravidanza. Le donne incinte con una storia di forte consumo di alcol vengono reclutate nello studio e randomizzate per ricevere o il breve intervento incentrato sull’astinenza dall’alcol o l’assistenza prenatale standard. Il risultato di interesse è la ricaduta nel bere. Le donne vengono reclutate nello studio a circa 18 settimane di gestazione e seguite nel corso della gravidanza fino al parto (circa 39 settimane di gestazione). I dati sono mostrati di seguito e indicano se le donne ricadono nel bere e, in caso affermativo, il momento della loro prima bevuta misurata in numero di settimane dalla randomizzazione. Per le donne che non ricadono, registriamo il numero di settimane dalla randomizzazione in cui sono rimaste senza alcol.

Cura prenatale standard			Intervento breve
Ricaduta	Nessuna ricaduta		Ricaduta	Nessuna ricaduta
19	20		16	21
6	19		21	15
5	17		7	18
4	14			18
				5

La domanda di interesse è se c’è una differenza nel tempo di ricaduta tra le donne assegnate alle cure prenatali standard rispetto a quelle assegnate all’intervento breve.

• Step 1.

Fissare le ipotesi e determinare il livello di significatività.

H0: Il tempo senza ricadute è identico tra i gruppi rispetto a

H1: Il tempo senza ricadute non è identico tra i gruppi (α=0,05)

• Step 2.

Selezionare la statistica del test appropriata.

La statistica del test per il log rank test è

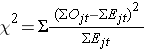
• Passo 3.

Imposta la regola di decisione.

La statistica del test segue una distribuzione chi-quadro, e quindi troviamo il valore critico nella tabella dei valori critici per la distribuzione Χ2) per df=k-1=2-1=1 e α=0,05. Il valore critico è 3,84 e la regola di decisione è di rifiutare H0 se Χ2 > 3,84.

• Passo 4.

Computare la statistica del test.

Per calcolare la statistica del test, organizziamo i dati secondo i tempi di evento (ricaduta) e determiniamo il numero di donne a rischio in ogni gruppo di trattamento e il numero che ricade in ogni tempo di ricaduta osservato. Nella tabella seguente, il gruppo 1 rappresenta le donne che ricevono le cure prenatali standard e il gruppo 2 le donne che ricevono l’intervento breve.

Tempo, Settimane	Numero a rischio – Gruppo 1 N1t	Numero a rischio – Gruppo 2 N2t	Numero di ricadute – Gruppo 1 O1t	Numero di ricadute – Gruppo 2 O2t
4	8	8	1	0
5	7	8	1	0
6	6	7	1	0
7	5	7	0	1
16	4	5	0	1
19	3	2	1	0
21	0	2	0	1

Poi sommiamo il numero a rischio, 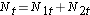, ad ogni tempo di evento, il numero di eventi osservati (ricadute), 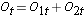, ad ogni tempo di evento e determiniamo il numero atteso di ricadute in ogni gruppo ad ogni tempo di evento usando 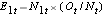e .

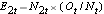Sommiamo poi i numeri osservati di eventi in ogni gruppo (ΣO1t e ΣO2t) e i numeri attesi di eventi in ogni gruppo (ΣE1t e ΣE2t) nel tempo. I calcoli per i dati di questo esempio sono mostrati di seguito.

Tempo, Settimane	Numero a rischio Gruppo 1 N1t	Numero a rischio Gruppo 2 N2t	Numero totale a rischio Nt	Numero di ricadute Gruppo 1 O1t	Numero di ricadute Gruppo 2 O2t	Numero totale di ricadute Ot	Numero previsto di ricadute nel gruppo 1	Numero previsto di ricadute nel gruppo 2
4	8	8	16	1	0	1	0.500	0.500
5	7	8	15	1	0	1	0.467	0.533
6	6	7	13	1	0	1	0.462	0.538
7	5	7	12	0	1	1	0.417	0.583
16	4	5	9	0	1	1	0.444	0.556
19	3	2	5	1	0	1	0.600	0.400
21	0	2	2	0	1	1	0.000	1.000
				4	3		2.890	4.110

Ora calcoliamo la statistica del test:

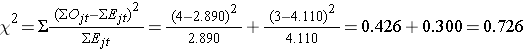
• Step 5.

Conclusione. Non rifiutare H0 perché 0,726 < 3,84. Non abbiamo prove statisticamente significative a α=0,05, per mostrare che il tempo alla ricaduta è diverso tra i gruppi.

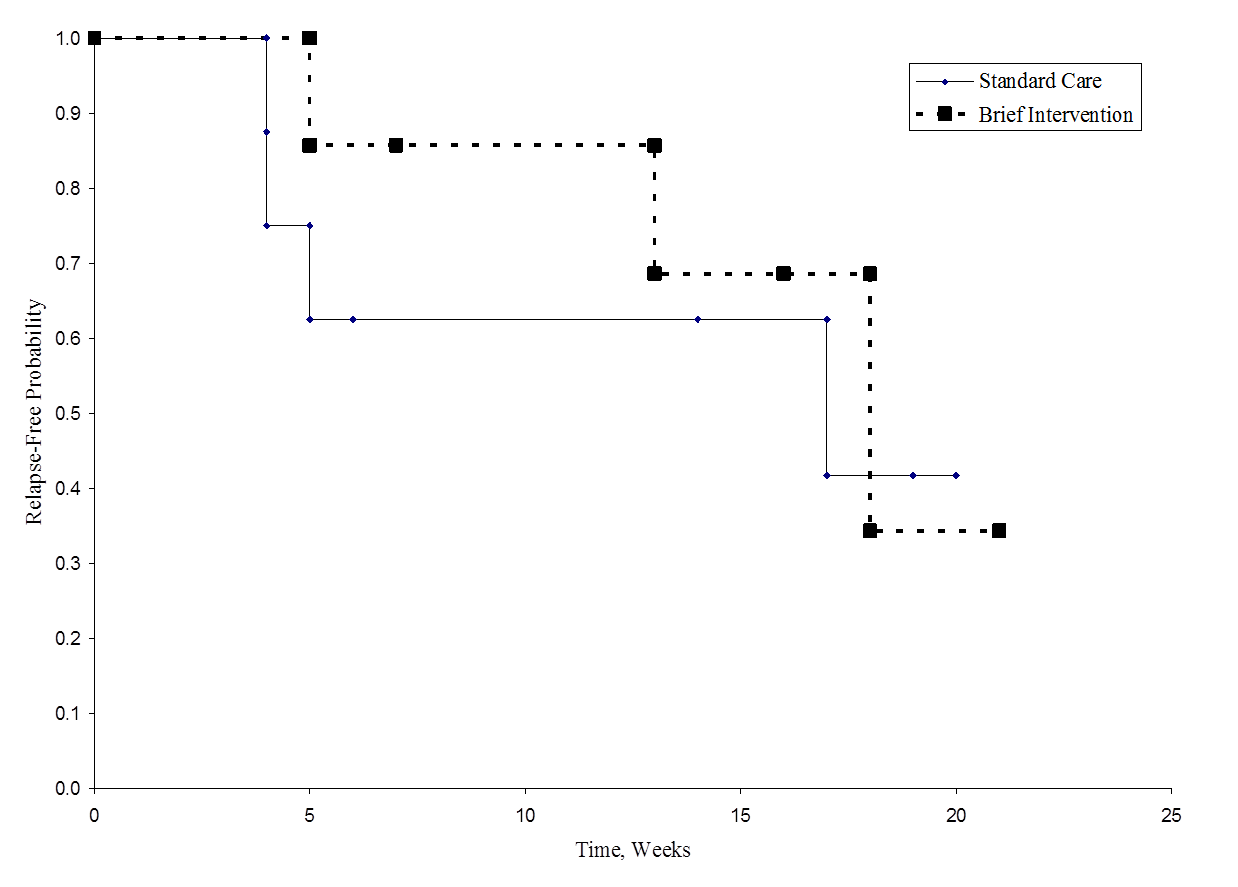
La figura sottostante mostra la sopravvivenza (tempo libero da ricaduta) in ogni gruppo. Si noti che le curve di sopravvivenza non mostrano molta separazione, coerente con i risultati non significativi nel test di ipotesi.

Tempo libero da ricaduta in ogni gruppo

Come notato, ci sono diverse varianti della statistica log rank. Alcuni pacchetti di calcolo statistico usano la seguente statistica per il log rank test per confrontare due gruppi indipendenti:

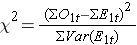
dove ΣO1t è la somma del numero osservato di eventi nel gruppo 1, e ΣE1t è la somma del numero atteso di eventi nel gruppo 1 preso su tutti i tempi degli eventi. Il denominatore è la somma delle varianze dei numeri attesi di eventi in ogni momento dell’evento, che viene calcolata come segue:

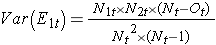
Esistono altre versioni della statistica log rank così come altri test per confrontare le funzioni di sopravvivenza tra gruppi indipendenti.7-9 Per esempio, un test popolare è il test di Wilcoxon modificato che è sensibile a differenze più grandi nei rischi all’inizio rispetto a quelli più tardi nel follow-up.10

ritorno all’inizio | pagina precedente | pagina successiva