
Anche se, come menzionato nella sezione Analisi del flusso di segnale, una qualche forma di analisi del flusso di segnale è il modo più generale di trattare l’amplificatore negative-feedback, la rappresentazione come due porte è l’approccio più spesso presentato nei libri di testo ed è presentato qui. Mantiene una partizione del circuito a due blocchi dell’amplificatore, ma permette ai blocchi di essere bilaterali. Alcuni svantaggi di questo metodo sono descritti alla fine.
Gli amplificatori elettronici usano corrente o tensione come ingresso e uscita, quindi sono possibili quattro tipi di amplificatori (uno qualsiasi dei due possibili ingressi con una qualsiasi delle due possibili uscite). Vedi classificazione degli amplificatori. L’obiettivo dell’amplificatore di retroazione può essere uno qualsiasi dei quattro tipi di amplificatore e non è necessariamente lo stesso tipo dell’amplificatore ad anello aperto, che a sua volta può essere uno qualsiasi di questi tipi. Così, per esempio, un amplificatore operazionale (amplificatore di tensione) può essere organizzato per fare invece un amplificatore di corrente.
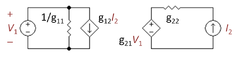
Gli amplificatori a retroazione negativa di qualsiasi tipo possono essere implementati usando combinazioni di reti a due porte. Ci sono quattro tipi di reti a due porte, e il tipo di amplificatore desiderato detta la scelta delle due porte e la selezione di una delle quattro diverse topologie di connessione mostrate nel diagramma. Queste connessioni sono di solito indicate come connessioni in serie o shunt (parallele). Nel diagramma, la colonna di sinistra mostra gli ingressi shunt; la colonna di destra mostra gli ingressi serie. La fila superiore mostra le uscite in serie; la fila inferiore mostra le uscite in derivazione. Le varie combinazioni di connessioni e le due porte sono elencate nella tabella sottostante.
| Tipo di amplificatore di feedback | Collegamento degli ingressi | Collegamento delle uscite | Responsabilità ideale | Dueport feedback |
|---|---|---|---|---|
| Corrente | Shunt | Serie | CCCS | g-parametro |
| Trasistenza | Shunt | Shunt | CCVS | y-parametro |
| Transconduttanza | Serie | Serie | VCCS | z-parametro |
| Tensione | Serie | Shunt | VCVVS | parametro h |
Per esempio, per un amplificatore a retroazione di corrente, la corrente dall’uscita viene campionata per la retroazione e combinata con la corrente all’ingresso. Pertanto, la retroazione viene idealmente eseguita utilizzando una sorgente di corrente (di uscita) controllata dalla corrente (CCCS), e la sua realizzazione imperfetta utilizzando una rete a due porte deve anche incorporare un CCCS, cioè, la scelta appropriata per la rete di retroazione è un g-parametro a due porte. Qui viene presentato il metodo a due porte utilizzato nella maggior parte dei libri di testo, utilizzando il circuito trattato nell’articolo sul modello di guadagno asintotico.

La figura 3 mostra un amplificatore a due transistor con una resistenza di retroazione Rf. Lo scopo è quello di analizzare questo circuito per trovare tre elementi: il guadagno, l’impedenza di uscita guardando l’amplificatore dal carico e l’impedenza di ingresso guardando l’amplificatore dalla sorgente.
- Sostituzione della rete di retroazione con una a due porteModifica
- Circuito a piccolo segnaleModifica
- Guadagno ad anello aperto caricoModifica
- Guadagno con feedbackEdit
- Resistenze di ingresso e di uscitaModifica
- Informazioni sulla determinazione della resistenzaModifica
- Applicazione all’esempio di amplificatoreModifica
- Tensione di carico e corrente di caricoModifica
Sostituzione della rete di retroazione con una a due porteModifica
Il primo passo è la sostituzione della rete di retroazione con una a due porte. Quali componenti vanno nella due porte?
Sul lato d’ingresso della due porte abbiamo Rf. Se la tensione al lato destro di Rf cambia, cambia la corrente in Rf che viene sottratta alla corrente che entra nella base del transistor di ingresso. Cioè, il lato d’ingresso della due porte è una sorgente di corrente dipendente controllata dalla tensione in cima al resistore R2.
Si potrebbe dire che il secondo stadio dell’amplificatore è solo un inseguitore di tensione, che trasmette la tensione al collettore del transistor d’ingresso alla cima di R2. Cioè, il segnale di uscita monitorato è davvero la tensione al collettore del transistor di ingresso. Questo punto di vista è legittimo, ma allora lo stadio di inseguitore di tensione diventa parte della rete di feedback. Questo rende l’analisi del feedback più complicata.
Una visione alternativa è che la tensione in cima a R2 è impostata dalla corrente di emettitore del transistor di uscita. Questa visione porta ad una rete di retroazione interamente passiva composta da R2 e Rf. La variabile che controlla il feedback è la corrente di emettitore, quindi il feedback è una sorgente di corrente controllata dalla corrente (CCCS). Cerchiamo tra le quattro reti a due porte disponibili e troviamo che l’unica con un CCCS è la g-parametro a due porte, mostrata in Figura 4. Il prossimo compito è quello di selezionare i parametri g in modo che la due porte di Figura 4 sia elettricamente equivalente alla sezione L composta da R2 e Rf. Questa selezione è una procedura algebrica fatta molto semplicemente guardando due casi individuali: il caso con V1 = 0, che rende il VCVS sul lato destro della due porte un cortocircuito; e il caso con I2 = 0. che rende il CCCS sul lato sinistro un circuito aperto. L’algebra in questi due casi è semplice, molto più facile che risolvere per tutte le variabili in una volta. La scelta dei parametri g che fanno sì che la sezione a due porte e quella a L si comportino allo stesso modo è mostrata nella tabella qui sotto.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{\mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 + R f {\displaystyle -{\frac {R_{2}{R_{2}+R_{mathrm {f} }}}}
 |
R 2 R 2 + R f {\displaystyle {\frac {R_{2}{R_{2}+R_{mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
 |
Circuito a piccolo segnaleModifica
Il prossimo passo è disegnare lo schema a piccolo segnale per l’amplificatore con le due porte al loro posto usando il modello ibrido-pi per i transistor. La figura 5 mostra lo schema con la notazione R3 = RC2 // RL e R11 = 1 / g11, R22 = g22.
Guadagno ad anello aperto caricoModifica
La figura 3 indica il nodo di uscita, ma non la scelta della variabile di uscita. Una scelta utile è l’uscita di corrente di cortocircuito dell’amplificatore (che porta al guadagno di corrente di cortocircuito). Poiché questa variabile porta semplicemente a una qualsiasi delle altre scelte (per esempio, tensione di carico o corrente di carico), il guadagno della corrente di cortocircuito viene trovato qui sotto.
Prima viene trovato il guadagno ad anello aperto caricato. La retroazione è spenta impostando g12 = g21 = 0. L’idea è di trovare quanto il guadagno dell’amplificatore è cambiato a causa delle resistenze nella rete di retroazione da sole, con la retroazione spenta. Questo calcolo è abbastanza facile perché R11, RB e rπ1 sono tutti in parallelo e v1 = vπ. Sia R1 = R11 // RB // rπ1. Inoltre, i2 = -(β+1) iB. Il risultato per il guadagno di corrente ad anello aperto AOL è:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\an8}A_{mathrm {OL} ={frac {beta i_{mathrm {B} i_{{mathrm {S} =g_{m}R_{mathrm {C} {\frac {\frac {beta }{beta +1}}}destra)\frac {R_{1}{R_{22}+{frac {r_{\frac {\frac 2}+R_{mathrm {C} {{beta +1}}}}\right)\ .\}

Guadagno con feedbackEdit
Nell’approccio classico al feedback, il feedforward rappresentato dal VCVS (cioè g21 v1) è trascurato. Questo fa sì che il circuito della Figura 5 assomigli allo schema a blocchi della Figura 1, e il guadagno con retroazione è quindi:
A F B = A O L 1 + β F B A O L {\displaystyle A_{mathrm {FB} =={frac {A_{mathrm {OL} 1+beta {{{mathrm {FB} A_{mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {{displaystyle A_{mathrm {FB} ={frac {A_{mathrm {OL} 1+{frac {R_{2}{R_{2}+R_{mathrm {f} A_{mathrm {OL}
Resistenze di ingresso e di uscitaModifica

Il feedback è usato per abbinare meglio le sorgenti di segnale ai loro carichi. Per esempio, una connessione diretta di una sorgente di tensione a un carico resistivo può comportare una perdita di segnale dovuta alla divisione della tensione, ma l’interiezione di un amplificatore a retroazione negativa può aumentare il carico apparente visto dalla sorgente, e ridurre l’impedenza apparente del driver vista dal carico, evitando l’attenuazione del segnale dalla divisione della tensione. Questo vantaggio non è limitato agli amplificatori di tensione, ma miglioramenti analoghi nell’accoppiamento possono essere organizzati per gli amplificatori di corrente, gli amplificatori di transconduttanza e gli amplificatori di transresistenza.
Per spiegare questi effetti del feedback sulle impedenze, prima una digressione su come la teoria delle due porte si avvicina alla determinazione della resistenza, e poi la sua applicazione all’amplificatore in questione.
Informazioni sulla determinazione della resistenzaModifica
La figura 6 mostra un circuito equivalente per trovare la resistenza d’ingresso di un amplificatore di tensione di retroazione (a sinistra) e per un amplificatore di corrente di retroazione (a destra). Queste disposizioni sono tipiche applicazioni del teorema di Miller.
Nel caso dell’amplificatore di tensione, la tensione di uscita βVout della rete di retroazione è applicata in serie e con una polarità opposta alla tensione di ingresso Vx che viaggia sul circuito (ma rispetto alla terra, le polarità sono le stesse). Di conseguenza, la tensione effettiva e la corrente che attraversa la resistenza d’ingresso dell’amplificatore Rin diminuiscono e la resistenza d’ingresso del circuito aumenta (si potrebbe dire che Rin aumenta apparentemente). Il suo nuovo valore può essere calcolato applicando il teorema di Miller (per le tensioni) o le leggi fondamentali dei circuiti. Così la legge della tensione di Kirchhoff prevede:
V x = I x R i n + β v o u t , {displaystyle V_{x}=I_{x}R_{mathrm {in} +beta v_{{mathrm {\i} ,}

dove vout = Av vin = Av Ix Rin. Sostituendo questo risultato nell’equazione precedente e risolvendo per la resistenza d’ingresso dell’amplificatore di retroazione, il risultato è:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . R_{{mathrm{in} (fb)={frac {V_{x}}{I_{x}}==sinistra(1+beta A_{v}} destra)R_{mathrm {in} }\ .}

La conclusione generale di questo esempio e di un esempio simile per il caso della resistenza di uscita è: una connessione di retroazione in serie all’ingresso (uscita) aumenta la resistenza di ingresso (uscita) di un fattore ( 1 + β AOL ), dove AOL = guadagno ad anello aperto.
D’altra parte, per l’amplificatore di corrente, la corrente di uscita βIout della rete di retroazione è applicata in parallelo e con una direzione opposta alla corrente di ingresso Ix. Come risultato, la corrente totale che scorre attraverso l’ingresso del circuito (non solo attraverso la resistenza d’ingresso Rin) aumenta e la tensione attraverso di essa diminuisce in modo che la resistenza d’ingresso del circuito diminuisce (Rin apparentemente diminuisce). Il suo nuovo valore può essere calcolato applicando il doppio teorema di Miller (per le correnti) o le leggi fondamentali di Kirchhoff:
I x = V i n R i n + β i o u t . {I_{x}={frac {V_{mathrm {in} {\a6}{R_{mathrm {in} +beta i_{\mathrm {\mathrm {out} }\ .}

dove iout = Ai iin = Ai Vx / Rin. Sostituendo questo risultato nell’equazione precedente e risolvendo per la resistenza d’ingresso dell’amplificatore di retroazione, il risultato è:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . R_{{mathrm{in} (fb)={frac {V_{x}{I_{x}}={frac {R_{mathrm {in}
Queste conclusioni possono essere generalizzate per trattare casi con azionamenti Norton o Thévenin arbitrari, carichi arbitrari e reti di retroazione generali a due porte. Tuttavia, i risultati dipendono dal fatto che l’amplificatore principale abbia una rappresentazione a due porte – cioè, i risultati dipendono dalla stessa corrente che entra ed esce dai terminali di ingresso, e allo stesso modo, la stessa corrente che lascia un terminale di uscita deve entrare nell’altro terminale di uscita.
Una conclusione più ampia, indipendente dai dettagli quantitativi, è che il feedback può essere utilizzato per aumentare o diminuire l’impedenza di ingresso e di uscita.
Applicazione all’esempio di amplificatoreModifica
Questi risultati di resistenza vengono ora applicati all’amplificatore della figura 3 e della figura 5. Il fattore di miglioramento che riduce il guadagno, cioè ( 1 + βFB AOL), decide direttamente l’effetto della retroazione sulle resistenze di ingresso e di uscita dell’amplificatore. Nel caso di una connessione shunt, l’impedenza d’ingresso si riduce di questo fattore; e nel caso di una connessione in serie, l’impedenza viene moltiplicata per questo fattore. Tuttavia, l’impedenza che viene modificata dalla retroazione è l’impedenza dell’amplificatore in Figura 5 con la retroazione disattivata, e include le modifiche all’impedenza causate dalle resistenze della rete di retroazione.
Pertanto, l’impedenza d’ingresso vista dalla sorgente con la retroazione disattivata è Rin = R1 = R11 // RB // rπ1, e con la retroazione attivata (ma senza feedforward)
R i n = R 1 1 + β F B A O L , {\displaystyle R_{\mathrm {in} R i n = R 1 1 + F B A O L = R 1 + F B A O L = R i n = R 1 1 + F B A O L = R i n = R 1 1 + F F B A O L A_{mathrm {OL}
L’impedenza vista dal carico necessita di ulteriori discussioni. Il carico in Figura 5 è collegato al collettore del transistor di uscita, e quindi è separato dal corpo dell’amplificatore dall’impedenza infinita della sorgente di corrente di uscita. Pertanto, la retroazione non ha alcun effetto sull’impedenza di uscita, che rimane semplicemente RC2 come si vede dalla resistenza di carico RL in Figura 3.
Se invece volessimo trovare l’impedenza presentata all’emettitore del transistor di uscita (invece che al suo collettore), che è collegato in serie alla rete di retroazione, la retroazione aumenterebbe questa resistenza del fattore di miglioramento ( 1 + βFB AOL).
Tensione di carico e corrente di caricoModifica
Il guadagno derivato sopra è il guadagno di corrente al collettore del transistor di uscita. Per mettere in relazione questo guadagno con il guadagno quando la tensione è l’uscita dell’amplificatore, si noti che la tensione di uscita al carico RL è legata alla corrente del collettore dalla legge di Ohm come vL = iC (RC2 || RL). Di conseguenza, il guadagno di transresistenza vL / iS si trova moltiplicando il guadagno di corrente per RC2 || RL:
v L i S = A F B ( R C 2 ∥ R L ) . {displaystyle {frac {v_{mathrm {L} i_{mathrm {S} {}=A_{mathrm {FB} (R_{mathrm {C2}}parallelo R_{mathrm {L}})} .}

Similmente, se si considera che l’uscita dell’amplificatore sia la corrente nella resistenza di carico RL, la divisione della corrente determina la corrente di carico, e il guadagno è quindi:
i L i S = A F B R C 2 R C 2 + R L. {\displaystyle {\frac {i_{mathrm {L} i i S =A_{mathrm {FB} {\frac {R_{mathrm {C2} {R_{mathrm {C2} +R_{mathrm {L} }}}\ .}

Seguono alcuni inconvenienti dell’approccio a due porte, destinati al lettore attento.
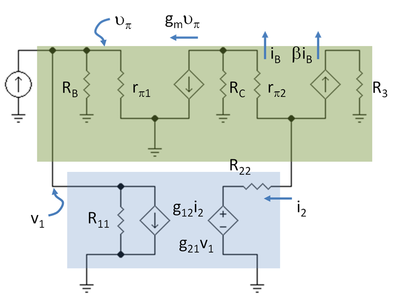
La figura 7 mostra lo schema a piccolo segnale con l’amplificatore principale e il feedback a due porte in caselle ombreggiate. Il feedback a due porte soddisfa le condizioni della porta: alla porta d’ingresso, Iin entra ed esce dalla porta, e allo stesso modo all’uscita, Iout entra ed esce.
Anche il blocco dell’amplificatore principale è a due porte? L’amplificatore principale è mostrato nella casella superiore ombreggiata. Le connessioni di terra sono etichettate. La figura 7 mostra il fatto interessante che l’amplificatore principale non soddisfa le condizioni della porta al suo ingresso e all’uscita a meno che le connessioni di terra siano scelte in modo che ciò accada. Per esempio, sul lato d’ingresso, la corrente che entra nell’amplificatore principale è IS. Questa corrente si divide in tre modi: alla rete di feedback, alla resistenza di bias RB e alla resistenza di base del transistor d’ingresso rπ. Per soddisfare la condizione di porta per l’amplificatore principale, tutti e tre i componenti devono essere restituiti al lato d’ingresso dell’amplificatore principale, il che significa che tutti i cavi di massa etichettati G1 devono essere collegati, così come il cavo emettitore GE1. Allo stesso modo, sul lato di uscita, tutti i collegamenti a terra G2 devono essere collegati e anche il collegamento a terra GE2. Quindi, nella parte inferiore dello schema, sotto il feedback a due porte e fuori dai blocchi dell’amplificatore, G1 è collegato a G2. Questo costringe le correnti di terra a dividersi tra i lati di ingresso e di uscita come previsto. Notate che questa disposizione dei collegamenti divide l’emettitore del transistor d’ingresso in un lato base e un lato collettore – una cosa fisicamente impossibile da fare, ma elettricamente il circuito vede tutte le connessioni di terra come un unico nodo, quindi questa finzione è permessa.
Ovviamente, il modo in cui i cavi di terra sono collegati non fa differenza per l’amplificatore (sono tutti un nodo), ma fa differenza per le condizioni della porta. Questa artificiosità è una debolezza di questo approccio: le condizioni di porta sono necessarie per giustificare il metodo, ma il circuito non è realmente influenzato da come le correnti sono scambiate tra le connessioni di terra.
Tuttavia, se nessuna disposizione possibile delle condizioni di terra porta alle condizioni di porta, il circuito potrebbe non comportarsi allo stesso modo. I fattori di miglioramento (1 + βFB AOL) per determinare l’impedenza di ingresso e di uscita potrebbero non funzionare. Questa situazione è imbarazzante, perché un fallimento di fare un due porte può riflettere un problema reale (semplicemente non è possibile), o riflettere una mancanza di immaginazione (per esempio, semplicemente non ha pensato di dividere il nodo emettitore in due). Di conseguenza, quando le condizioni della porta sono in dubbio, almeno due approcci sono possibili per stabilire se i fattori di miglioramento sono accurati: o simulare un esempio usando Spice e confrontare i risultati con l’uso di un fattore di miglioramento, o calcolare l’impedenza usando una sorgente di prova e confrontare i risultati.
Una scelta più pratica è quella di abbandonare del tutto l’approccio a due porte, e usare varie alternative basate sulla teoria del grafico del flusso di segnale, compreso il metodo Rosenstark, il metodo Choma, e l’uso del teorema di Blackman. Questa scelta può essere consigliabile se i modelli di dispositivi a piccolo segnale sono complessi o non sono disponibili (per esempio, i dispositivi sono conosciuti solo numericamente, forse da misurazioni o da simulazioni SPICE).
.