Az elektromágneses metaanyag olyan elektromágneses hullámokat befolyásol, amelyek a hullámhossznál kisebb hullámhosszú szerkezeti jellemzőire hatnak vagy azokkal kölcsönhatásba lépnek. Ahhoz, hogy egy effektív törésmutatóval pontosan leírható homogén anyagként viselkedjen, jellemzőinek a hullámhossznál jóval kisebbnek kell lenniük.
Mikrohullámú sugárzás esetén a jellemzők milliméteres nagyságrendűek. A mikrohullámú frekvenciájú metaanyagokat általában elektromosan vezető elemek (például dróthurkok) megfelelő induktív és kapacitív jellemzőkkel rendelkező tömbjeiként építik fel. Sok mikrohullámú metaanyag osztott gyűrűs rezonátorokat használ.
A fotonikus metaanyagok nanométeres skálán strukturáltak, és optikai frekvenciákon manipulálják a fényt. A fotonikus kristályok és a frekvenciaszelektív felületek, például a diffrakciós rácsok, dielektromos tükrök és optikai bevonatok hasonlóságot mutatnak a hullámhossz alatti strukturált metaanyagokkal. Ezeket azonban általában a metaanyagoktól különbözőnek tekintik, mivel funkciójuk diffrakcióból vagy interferenciából ered, és így nem közelíthetők meg homogén anyagként. Az olyan anyagi struktúrák, mint a fotonikus kristályok azonban a látható fényspektrumban hatékonyak. A látható spektrum közepének hullámhossza körülbelül 560 nm (a napfény esetében). A fotonikus kristályszerkezetek általában fele ekkora vagy kisebb, azaz <280 nm-esek.
A plazmonikus metaanyagok felületi plazmonokat használnak, amelyek olyan elektromos töltéscsomagok, amelyek kollektívan rezegnek a fémek felületén optikai frekvenciákon.
A frekvenciaszelektív felületek (FSS) hullámhossz alatti jellemzőket mutathatnak, és különbözőképpen mesterséges mágneses vezetőként (AMC) vagy nagy impedanciájú felületként (HIS) ismertek. Az FSS-ek induktív és kapacitív jellemzőket mutatnak, amelyek közvetlenül kapcsolódnak a hullámhossz alatti szerkezetükhöz.
Az elektromágneses metaanyagok különböző osztályokba sorolhatók, az alábbiak szerint:
Negatív törésmutatóSzerkesztés
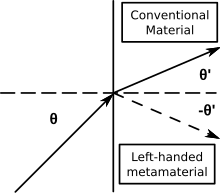
A negatív indexű metaanyagokat (NIM) negatív törésmutató jellemzi. A NIM-ek más elnevezései közé tartozik a “balkezes közeg”, a “negatív törésmutatójú közeg” és a “visszahullámzó közeg”. Azokat a NIM-eket, ahol a negatív törésmutató egyidejűleg negatív permittivitásból és negatív permeabilitásból adódik, kettős negatív metaanyagoknak vagy kettős negatív anyagoknak (DNG) is nevezik.
A valós permittivitással és permeabilitással jól közelíthető anyagot feltételezve, a ϵ r {\displaystyle \epsilon _{r}} permittivitás közötti összefüggés.

, áteresztőképesség μ r {\displaystyle \mu _{r}}

és a törésmutató n az n = ± ϵ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{\mathrm {r} }\mu _{\mathrm {r} }}}}

. Minden ismert nem-metamateriális átlátszó anyag (üveg, víz, …) rendelkezik pozitív ϵ r {\displaystyle \epsilon _{r}}

és μ r {\displaystyle \mu _{r}}

. A konvenció szerint n esetében a pozitív négyzetgyököt használjuk. Egyes mesterséges metaanyagoknál azonban ϵ r {\displaystyle \epsilon _{r}}

és μ r < 0 {\displaystyle \mu _{r}<0}

. Mivel a ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}} szorzata ϵ r {\displaystyle \epsilon _{r}}

pozitív, n valós. Ilyen körülmények között n negatív négyzetgyökét kell venni. Ha mindkettő ϵ r {\displaystyle \epsilon _{r}}

és μ r {\displaystyle \mu _{r}}

pozitív (negatív), a hullámok előre (hátra) irányban terjednek. Az elektromágneses hullámok nem terjedhetnek olyan anyagokban, amelyek ϵ r {\displaystyle \epsilon _{r}}

és μ r {\displaystyle \mu _{r}}

ellentétes előjelű, ahogy a törésmutató képzeletbeli értékké válik. Az ilyen anyagok átlátszatlanok az elektromágneses sugárzás számára, és példaként említhetők a plazmonikus anyagok, például a fémek (arany, ezüst, …).
A fenti megfontolások leegyszerűsítőek a tényleges anyagok esetében, amelyeknek komplex értékű ϵ r {\displaystyle \epsilon _{r}} komplex értékkel kell rendelkezniük.

és μ r {\displaystyle \mu _{r}}

. Mindkét ϵ r {\displaystyle \epsilon _{r}} valós részei

és μ r {\displaystyle \mu _{r}}

nem kell negatívnak lenniük ahhoz, hogy egy passzív anyag negatív fénytörést mutasson. Sőt, a negatív törésmutató körkörösen polarizált hullámok esetén a kiralitásból is adódhat. A negatív n értékű metaanyagok számos érdekes tulajdonsággal rendelkeznek:
- A Snell-törvény (n1sinθ1 = n2sinθ2) továbbra is leírja a fénytörést, de mivel az n2 negatív, a beeső és a megtörött sugarak a felületi normálisnak ugyanazon az oldalán vannak a pozitív és negatív indexű anyagok határfelületén.
- A Cherenkov-sugárzás a másik irányba mutat.
- Az időátlagolt Poynting-vektor a fázissebességgel antiparallel. A hullámok (energia) terjedéséhez azonban egy -µ-nek egy -ε-vel kell párosulnia, hogy az anyagparaméterektől függő hullámszám-függés k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }}}
.
A negatív törésmutató matematikailag az E, H és k vektorhármasból ered.
Elektromágneses metaanyagokban terjedő síkhullámok esetén az elektromos tér, a mágneses tér és a hullámvektor balkezes szabályt követ, ami a hagyományos optikai anyagok viselkedésének fordítottja.
Mostanáig csak a metaanyagok mutatnak negatív törésmutatót.
Egyetlen negatívSzerkesztés
Az egyetlen negatív (SNG) metaanyagok vagy negatív relatív áteresztőképességgel (εr) vagy negatív relatív permeabilitással (µr) rendelkeznek, de nem mindkettővel. Ezek egy másik, kiegészítő SNG-vel kombinálva metaanyagként viselkednek, együttesen DNG-ként viselkednek.
Epszilon negatív közegek (ENG) negatív εr-t mutatnak, míg a µr pozitív. Számos plazma mutatja ezt a tulajdonságot. Például az olyan nemesfémek, mint az arany vagy az ezüst ENG az infravörös és a látható spektrumban.
Mu-negatív közegek (MNG) pozitív εr-t és negatív µr-t mutatnak. A gyrotropikus vagy gyromágneses anyagok mutatják ezt a tulajdonságot. A gyrotrópikus anyag olyan anyag, amelyet kvázisztatikus mágneses tér jelenléte megváltoztat, lehetővé téve a magnetooptikai hatást. A magnetooptikai hatás az a jelenség, amikor egy elektromágneses hullám egy ilyen közegben terjed. Egy ilyen anyagban a balra és jobbra forgó elliptikus polarizációk különböző sebességgel terjedhetnek. Amikor a fényt egy magnetooptikai anyagrétegen keresztül továbbítják, az eredményt Faraday-effektusnak nevezik: a polarizációs sík elforgatható, Faraday-rotátort képezve. Az ilyen tükröződés eredményét magnetooptikai Kerr-effektusnak nevezik (nem tévesztendő össze a nemlineáris Kerr-effektussal). Két olyan gyrotropikus anyagot, amelyekben a két fő polarizáció forgásiránya megfordult, optikai izomereknek nevezünk.
Egy ENG anyagból és egy MNG anyagból készült lemez összekapcsolása olyan tulajdonságokat eredményezett, mint a rezonancia, az anomális alagút, az átlátszóság és a nulla reflexió. A negatív indexű anyagokhoz hasonlóan az SNG-k is eredendően diszperzívek, így εr, µr és n törésmutatójuk a frekvencia függvénye.
HyperbolicEdit
A hyperbolic metaanyagok (HMM) a negatív és pozitív permittivitás-tenzor komponensei miatt bizonyos polarizáció vagy fényterjedési irány esetén fémként viselkednek, a másik esetén pedig dielektrikumként viselkednek, ami extrém anizotrópiát eredményez. Az anyag diszperziós viszonya a hullámvektortérben hiperboloidot alkot, ezért hiperbolikus metaanyagnak nevezik. A HMM-ek szélsőséges anizotrópiája a fény irányított terjedéséhez vezet a felületen belül és a felületen. A HMM-ek számos alkalmazási lehetőséget mutattak, például érzékelés, képalkotás, optikai jelek irányítása, fokozott plazmon-rezonancia hatások.
BandgapEdit
Elektromágneses sávhatár metaanyagok (EBG vagy EBM) szabályozzák a fény terjedését. Ezt vagy fotonikus kristályokkal (PC) vagy balkezes anyagokkal (LHM) érik el. A PC-k teljesen meg tudják tiltani a fény terjedését. Mindkét osztály lehetővé teszi, hogy a fény meghatározott, tervezett irányokban terjedjen, és mindkettő tervezhető a kívánt frekvenciájú sávhatárokkal. Az EBG-k periódusmérete a hullámhossz jelentős hányada, ami konstruktív és destruktív interferenciát hoz létre.
A PC-ket megkülönböztetik a hullámhossz alatti szerkezetektől, például a hangolható metaanyagoktól, mivel a PC tulajdonságait sávhézagjellemzőiből eredeztetik. A PC-k a fény hullámhosszának megfelelő méretűek, szemben más metaanyagokkal, amelyek szubhullámhosszú struktúrát tárnak fel. Továbbá a PC-k a fény diffrakciójával működnek. Ezzel szemben a metaanyag nem használ diffrakciót.
A PC-k periodikus zárványokkal rendelkeznek, amelyek a zárványok szórásból eredő destruktív interferenciája miatt gátolják a hullámterjedést. A PC-k fotonikus sávhézag-tulajdonsága az elektronikus félvezető kristályok elektromágneses analógjává teszi őket.
AzEBG-k célja a jó minőségű, alacsony veszteségű, periodikus, dielektromos szerkezetek létrehozása. Egy EBG ugyanúgy hat a fotonokra, mint a félvezető anyagok az elektronokra. A PC-k tökéletes sávhézagos anyagok, mert nem engedik a fény terjedését. Az előírt periodikus struktúra minden egyes egysége úgy viselkedik, mint egy atom, bár sokkal nagyobb méretű.
Az EBG-ket úgy tervezték, hogy bizonyos érkezési szögek és polarizációk esetén megakadályozzák egy kijelölt frekvenciasávszélesség terjedését. Az EBG különleges tulajdonságainak előállítására különböző geometriákat és szerkezeteket javasoltak. A gyakorlatban lehetetlen hibátlan EBG eszközt építeni.
EBG-ket néhány gigahertztől (GHz) néhány terahertzig (THz) terjedő frekvenciákon, rádió, mikrohullámú és közép-infravörös frekvenciatartományokban gyártottak. Az EBG alkalmazási fejlesztések közé tartozik az átviteli vonal, a négyzet alakú dielektromos rudakból készült faoszlopok és számos különböző típusú, alacsony nyereségű antenna.
Kettős pozitív közegSzerkesztés
A természetben előfordulnak kettős pozitív közegek (DPS), például a természetben előforduló dielektrikumok. A permittivitás és a mágneses permeabilitás egyaránt pozitív, és a hullámterjedés előrefelé történik. Olyan mesterséges anyagokat állítottak elő, amelyek egyesítik a DPS, ENG és MNG tulajdonságokat.
Bi-izotróp és bianizotrópSzerkesztés
A metaanyagok kettős vagy egyszeresen negatív, illetve kettős pozitív kategóriába sorolása általában feltételezi, hogy a metaanyagnak független elektromos és mágneses válaszai vannak, amelyeket ε és µ ír le. Sok esetben azonban az elektromos tér mágneses polarizációt okoz, míg a mágneses tér elektromos polarizációt indukál, amit magnetoelektromos csatolásnak nevezünk. Az ilyen közegeket bi-izotrópnak nevezzük. Azokat a közegeket, amelyek mágneses-elektromos csatolást mutatnak, és anizotrópok (ami számos metamateriális struktúrára jellemző), bi-anisotrópnak nevezzük.
A bi-izotróp közegek mágneses-elektromos csatolásának négy anyagi paramétere a sajátja. Ezek az elektromos (E) és a mágneses (H) térerősség, valamint az elektromos (D) és a mágneses (B) fluxussűrűség. Ezek a paraméterek ε, µ, κ és χ, illetve a permittivitás, a permeabilitás, a kiralitás erőssége és a Tellegen-paraméter. Az ilyen típusú közegekben az anyagi paraméterek nem változnak a mérések elforgatott koordinátarendszere mentén bekövetkező változásokkal. Ebben az értelemben invariánsak vagy skalárisak.
A belső magnetoelektromos paraméterek, κ és χ, befolyásolják a hullám fázisát. A kiralitás paraméter hatása a törésmutató felosztása. Izotróp közegekben ez csak akkor eredményez hullámterjedést, ha ε és µ azonos előjelű. Bi-izotróp közegekben, ahol χ-t nullának, κ-t pedig nem nulla értékűnek feltételezzük, eltérő eredmények adódnak. Vagy visszafelé irányuló hullám, vagy előre irányuló hullám keletkezhet. Alternatívaként két előre irányuló hullám vagy két hátrafelé irányuló hullám is előfordulhat, a kiralitásparaméter erősségétől függően.
Az általános esetben a bi-izotróp anyagok konstitutív összefüggései a következők: D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}

ahol ϵ {\displaystyle \epsilon }

és μ{\displaystyle \mu }

a permittivitás-, illetve a permeabilitás-tenzor, míg ξ {\displaystyle \xi }

és ζ {\displaystyle \zeta }

a két magneto-elektromos tenzor. Ha a közeg reciprok, a permittivitás és a permeabilitás szimmetrikus tenzorok, és ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}

, ahol κ {\displaystyle \kappa } {\displaystyle \kappa }

a királis elektromágneses és reciprok mágneses-elektromos választ leíró királis tenzor. A királis tenzor a következőképpen fejezhető ki: κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}

, ahol tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

a κ {\displaystyle \kappa } nyomvonala.

, I az azonossági mátrix, N egy szimmetrikus nyomvonalmentes tenzor, J pedig egy antiszimmetrikus tenzor. Az ilyen felbontás lehetővé teszi a reciprok bianizotróp válasz osztályozását, és a következő három fő osztályt azonosíthatjuk: (i) királis közegek ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}

), (ii) pszeudokirális közegek ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )=0,N\neq 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}

).
ChiralEdit
A metaanyagok kezessége potenciális zavarforrás, mivel a metaanyag irodalomban a bal- és jobbkezes kifejezések két, egymásnak ellentmondó használatát találjuk. Az első a két cirkulárisan polarizált hullám egyikére utal, amelyek a királis közegekben a terjedési módusok. A második az elektromos mező, a mágneses mező és a Poynting-vektor hármasára vonatkozik, amely negatív törésmutatójú közegekben keletkezik, amelyek a legtöbb esetben nem királisak.
A királis és/vagy bianizotróp elektromágneses válasz általában a 3D geometriai kiralitás következménye: a 3D-királis metaanyagok 3D-királis struktúrák gazdamédiumba ágyazásával állnak össze, és kiralitással kapcsolatos polarizációs hatásokat, például optikai aktivitást és cirkuláris dichroizmust mutatnak. Létezik a 2D kiralitás fogalma is, és egy síkbeli tárgyat akkor mondjuk királisnak, ha nem lehet tükörképére szuperponálni, hacsak nem emeljük ki a síkból. Az anizotróp és veszteséges 2D-királis metaanyagoknál megfigyelték, hogy a cirkulárisan polarizált hullámok cirkuláris konverziós dichroszimának köszönhetően irányítottan aszimmetrikus transzmissziót (reflexiót, abszorpciót) mutatnak. Másfelől bianizotróp válasz keletkezhet olyan geometriai achirális struktúrákból, amelyek nem rendelkeznek sem 2D, sem 3D belső kiralitással. Plum és munkatársai vizsgálták az extrinsic chiralitás miatti mágneses-elektromos csatolást, amikor egy (achirális) struktúra elrendezése a sugárzási hullámvektorral együtt eltér a tükörképétől, és nagy, hangolható lineáris optikai aktivitást, nemlineáris optikai aktivitást, tükrös optikai aktivitást és cirkuláris konverziós dichroizmust figyeltek meg. Rizza et al. 1D királis metaanyagokat javasoltak, ahol az effektív királis tenzor nem eltűnő, ha a rendszer geometriailag egydimenziós királis (a teljes struktúra tükörképe nem szuperponálható rá forgatás nélküli transzlációkkal).
3D-királis metaanyagok olyan királis anyagokból vagy rezonátorokból épülnek fel, amelyekben az effektív kiralitás paraméter κ {\displaystyle \kappa }

nem nulla. Az ilyen királis metaanyagokban a hullámterjedési tulajdonságok azt mutatják, hogy erős kiralitású és pozitív ϵ r {\displaystyle \epsilon _{r}} pozitív ϵ r {\displaystyle \epsilon _{r}} metaanyagokban negatív fénytörés is megvalósítható.

és μ r {\displaystyle \mu _{r}}

. Ennek oka, hogy a törésmutató n {\displaystyle n}

a bal és jobb oldali cirkulárisan polarizált hullámok esetében különböző értékeket vesz fel, amit a
n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}}\pm \kappa } ad meg.

Látható, hogy egy polarizáció esetén negatív index lép fel, ha κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}

. Ebben az esetben nem szükséges, hogy valamelyik vagy mindkét ϵ r {\displaystyle \epsilon _{r}}

és μ r {\displaystyle \mu _{r}} is.

negatív legyen a visszafelé irányuló hullámterjedés esetén. A kiralitás miatti negatív törésmutatót először Plum et al. és Zhang et al. figyelték meg egyszerre és egymástól függetlenül 2009-ben.
FSS alapúSzerkesztés
A frekvenciaszelektív felület alapú metaanyagok blokkolják a jeleket egy hullámsávban és átengedik azokat egy másik hullámsávban. A fix frekvenciájú metaanyagok alternatívájává váltak. Lehetővé teszik a frekvenciák opcionális változtatását egyetlen közegben, a fix frekvenciaválasz korlátozó korlátozásai helyett.
