Az általánosított lineáris modellek oktatóprogramban különböző GLM-eket ismertünk meg, mint például a lineáris regresszió, logisztikus regresszió stb. A TechVidvan R oktatósorozatának ebben az oktatóanyagában a lineáris regressziót fogjuk részletesen megvizsgálni R-ben. Megtanuljuk, mi az az R lineáris regresszió, és hogyan lehet megvalósítani az R-ben. Megnézzük a legkisebb négyzet becslési módszert, és azt is megtanuljuk, hogyan ellenőrizhetjük a modell pontosságát.

Szóval, minden további nélkül, kezdjük el!

Lineáris regresszió az R-ben

A lineáris regresszió az R-ben egy olyan módszer, amelyet egy vagy több bemeneti prediktor változó értéke(i) segítségével egy változó értékének előrejelzésére használunk. A lineáris regresszió célja, hogy lineáris kapcsolatot állítson fel a kívánt kimeneti változó és a bemeneti prediktorok között.

Modellezni egy folytonos változót Y egy vagy több bemeneti prediktor változó Xi függvényeként, hogy a függvény segítségével megjósolható legyen Y értéke, ha csak Xi értékei ismertek. Az ilyen lineáris összefüggés általános formája:

Y=?0+?1 X

Itt ?0 a metszéspont
és ?1 a meredekség.

A lineáris regresszió típusai az R-ben

A lineáris regressziónak két típusa van az R-ben:

• Simple Linear Regression
• Multiple Linear Regression

Nézzük meg ezeket egyenként.

Egyszerű lineáris regresszió R-ben

Az egyszerű lineáris regresszió célja két folytonos változó közötti lineáris kapcsolat megtalálása. Fontos megjegyezni, hogy az összefüggés statisztikai jellegű és nem determinisztikus.

A determinisztikus összefüggés az, ahol az egyik változó értéke a másik változó értéke alapján pontosan meghatározható. A determinisztikus kapcsolatra példa a kilométerek és a mérföldek közötti kapcsolat. A kilométer értékét felhasználva pontosan meg tudjuk találni a mérföldben kifejezett távolságot. A statisztikai kapcsolat nem pontos, és mindig van előrejelzési hibája. Például elegendő adat birtokában kapcsolatot találhatunk egy személy magassága és súlya között, de mindig lesz hibahatár, és léteznek kivételes esetek.

Az egyszerű lineáris regresszió lényege, hogy olyan egyenest találjunk, amely a legjobban illeszkedik a két változó adott értékeihez. Ez az egyenes aztán segíthet megtalálni a függő változó értékeit, ha azok hiányoznak.

Vizsgáljuk meg ezt egy példa segítségével. Van egy adathalmazunk, amely 500 ember magasságából és súlyából áll. A célunk itt az, hogy olyan lineáris regressziós modellt alkossunk, amely úgy fogalmazza meg a magasság és a súly közötti kapcsolatot, hogy amikor a magasságot(Y) adjuk meg bemenetként a modellnek, az minimális hibahatárral vagy hibával adhassa vissza nekünk a súlyt(X).

Y=b0+b1X

A b0 és b1 értékeit úgy kell megválasztani, hogy minimalizálják a hibahatárt. A hibamértékkel mérhetjük a modell pontosságát.

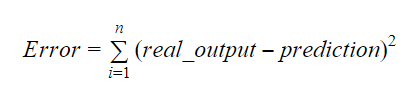
A meredekséget vagy a koefficienst így számolhatjuk ki: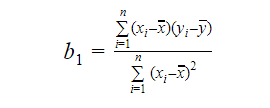

A b1 értéke betekintést ad a függő és a független változók közötti kapcsolat természetébe.

• Ha b1 > 0, akkor a változók között pozitív kapcsolat áll fenn, azaz. x növekedése y növekedését eredményezi.
• Ha b1 < 0, akkor a változók negatív kapcsolatban állnak, azaz x növekedése y csökkenését eredményezi.

A b0 vagy intercept értéke a következőképpen számítható ki: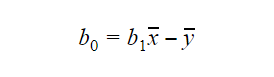
A b0 értéke is sok információt adhat a modellről és fordítva.

Ha a modellben nem szerepel x=0, akkor az előrejelzés b1 nélkül értelmetlen. Ahhoz, hogy a modellben bármely ponton csak b0 és ne legyen benne b1, az x értékének az adott ponton 0-nak kell lennie. Olyan esetekben, mint például a magasság, x nem lehet 0, és egy személy magassága nem lehet 0. Ezért egy ilyen modell értelmetlen csak b0-val.

Ha a b0 kifejezés hiányzik, akkor a modell áthalad az origón, ami azt jelenti, hogy az előrejelzés és a regressziós együttható(meredekség) torz lesz.

Multiple Linear Regression in R

A multiple lineáris regresszió az egyszerű lineáris regresszió kiterjesztése. A többszörös lineáris regresszióban olyan lineáris modell létrehozására törekszünk, amely több prediktor változó értékeinek felhasználásával képes megjósolni a célváltozó értékét. Egy ilyen függvény általános formája a következő:

Y=b0+b1X1+b2X2+…+bnXn

A modell pontosságának értékelése

A modell minőségének és pontosságának értékelésére különböző módszerek állnak rendelkezésre. Nézzünk meg egyesével néhány ilyen módszert.

R-négyzet

Az adatokban rejlő valódi információ a benne közvetített variancia. Az R-négyzet azt mondja meg, hogy a célváltozó (y) variációjának mekkora hányadát magyarázza a modell. Egy modell R-négyzet mértékét a következő képlet segítségével találhatjuk meg: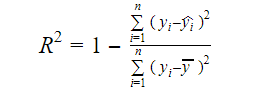

Hol,

• yi az y illesztett értéke az i megfigyeléshez
• y az Y átlaga.

Az R-négyzet alacsonyabb értéke a modell kisebb pontosságát jelzi. Az R-négyzet mérték azonban nem feltétlenül végső döntő tényező.

Adjustált R-négyzet

Amint nő a változók száma a modellben, úgy nő az R-négyzet értéke is. Ez hibákat okoz az újonnan hozzáadott változók által magyarázott variációban is. Ezért több változó esetén kiigazítjuk az R-négyzet képletét.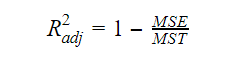
Itt az MSE az átlagos standard hibát jelenti, ami:

és az MST az átlagos standard összesen, ami a következő: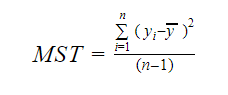

Hol, n a megfigyelések száma és q az együtthatók száma.

Az R-négyzet és a korrigált R-négyzet közötti kapcsolat: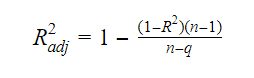

Standard hiba és F-statisztika

A standard hiba és az F-statisztika egyaránt a modell illeszkedésének minőségét mérik. A standard hiba és az F-statisztika képletei a következők:

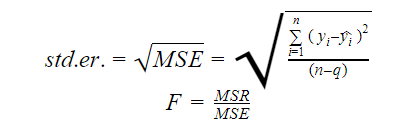
Ahol MSR a Mean Square Regression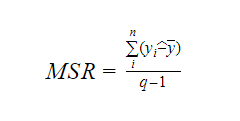

AIC és BIC

Akaike információs kritériuma és a Bayesian Information Criterion a statisztikai modellek illeszkedésének minőségét mérik. A modell kiválasztásának kritériumaiként is használhatók.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Hol,

• L a valószínűségi függvény,
• k a modell paramétereinek száma,
• n a minta mérete.

lm függvény az R-ben

Az R lm() függvénye lineáris modelleket illeszt. Regressziót, valamint variancia- és kovarianciaanalízist végezhet. Az lm függvény szintaxisa a következő:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Hol,

• formula egy “formula” osztályú objektum és az illesztendő modell szimbolikus reprezentációja,
• data az adatkeret vagy lista, amely a képletben szereplő változókat tartalmazza(data egy opcionális argumentum. Ha hiányzik, a függvény a környezetből veszi fel a változókat),
• subset egy opcionális vektor, amely az illesztési folyamatban felhasználandó megfigyelések részhalmazát tartalmazza,
• weights egy opcionális vektor, amely megadja az illesztési folyamatban használandó súlyokat,
• na.action egy függvény, amely megmutatja, hogy mi történjen, ha NA-kkal találkozunk az adatokban,
• method jelöli a modell illesztésének módszerét,
• model, x, y és qr logikai függvények, amelyek azt szabályozzák, hogy a megfelelő értékeket a kimenettel együtt kell-e visszaadni vagy sem. Ezek az értékek:
• model: a modellkeret
• x: a modellmátrix
• y: a válasz
• qr: a qr dekompozíció
• singular.ok egy logikai, amely azt vezérli, hogy a szinguláris illesztés megengedett-e vagy sem,
• offset egy előre ismert prediktor, amelyet a modellben használni kell,
• . . . további argumentumok, amelyeket át kell adni az alacsonyabb szintű regressziós függvényeknek.

Practical Example of Linear Regression in R

Egyelőre elég az elméletből. Nézzük meg, hogyan lehet mindezt megvalósítani. Egy lineáris modellt fogunk illeszteni lineáris regresszióval az R-ben az lm() függvény segítségével. Utána ellenőrizni fogjuk a modell illeszkedésének minőségét is. Használjuk a cars adatkészletet, amely alapértelmezés szerint az R alapcsomagban van megadva.

1. Kezdjük az adatkészlet grafikus elemzésével, hogy jobban megismerjük azt. Ehhez rajzoljunk egy szórásdiagramot, és ellenőrizzük, hogy mit árul el az adatokról.

A scatter.smooth() függvény segítségével létrehozhatjuk az adathalmaz szórásdiagramját.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Kimenet

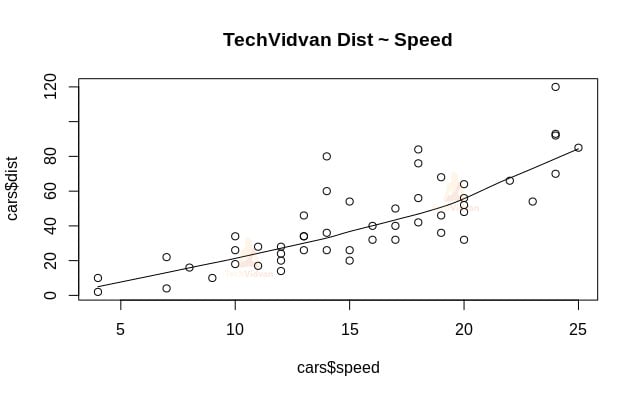
A szórásdiagram azt mutatja, hogy pozitív korreláció van a távolság és a sebesség között. Ez lineárisan növekvő kapcsolatra utal a két változó között. Ez alkalmassá teszi az adatokat lineáris regresszióra, mivel a lineáris kapcsolat az adatokra való lineáris modell illesztésének egyik alapfeltétele.

2. Most, hogy meggyőződtünk arról, hogy a lineáris regresszió alkalmas az adatokra, az lm() függvényt használhatjuk a lineáris modell illesztésére.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Kimenet

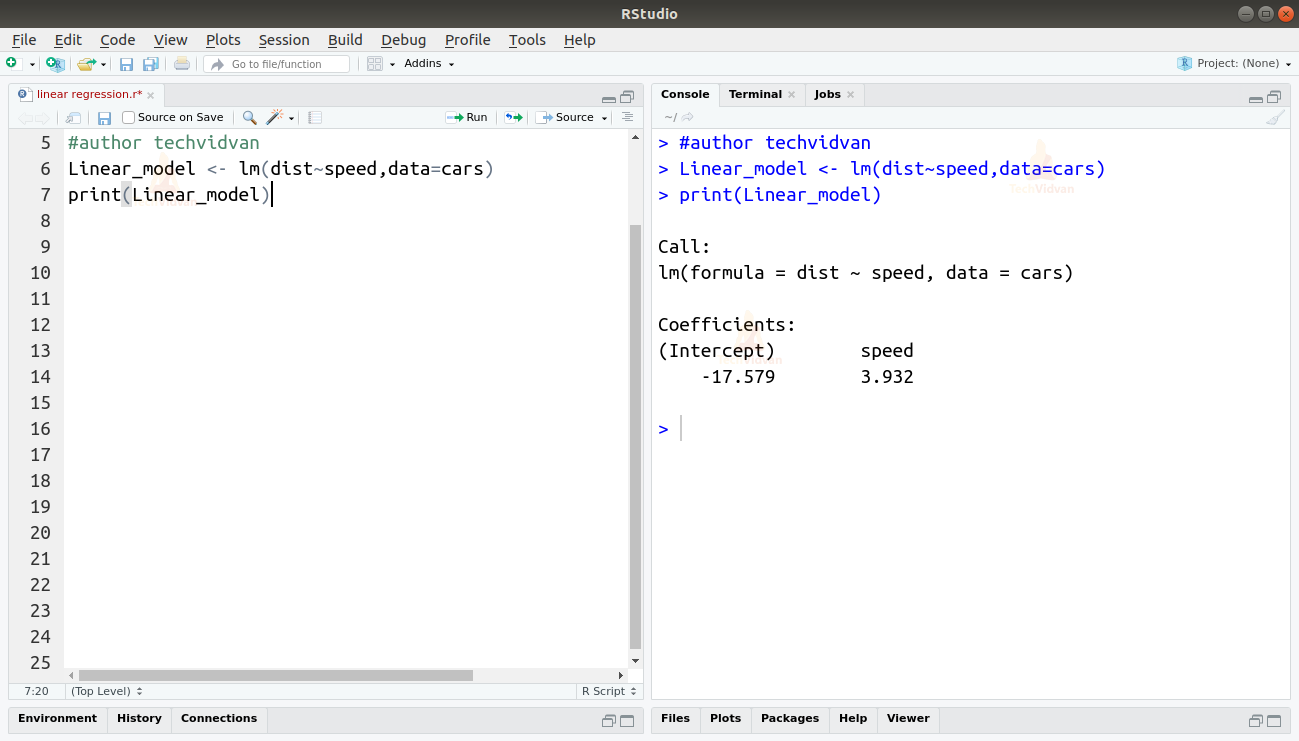
Az lm() függvény kimenete megmutatja nekünk a metszéspontot és a sebességi együtthatót. Így a távolság és a sebesség közötti lineáris kapcsolatot a következőképpen határozzuk meg:

Távolság=metszéspont+koefficiens*sebesség

Távolság=-17,579+3,932*sebesség

3. Most, hogy illesztettünk egy modellt, ellenőrizzük az illeszkedés minőségét vagy jóságát. Kezdjük a lineáris modell összegzésének ellenőrzésével a summary() függvény segítségével.

summary(Linear_model)

Kimenet

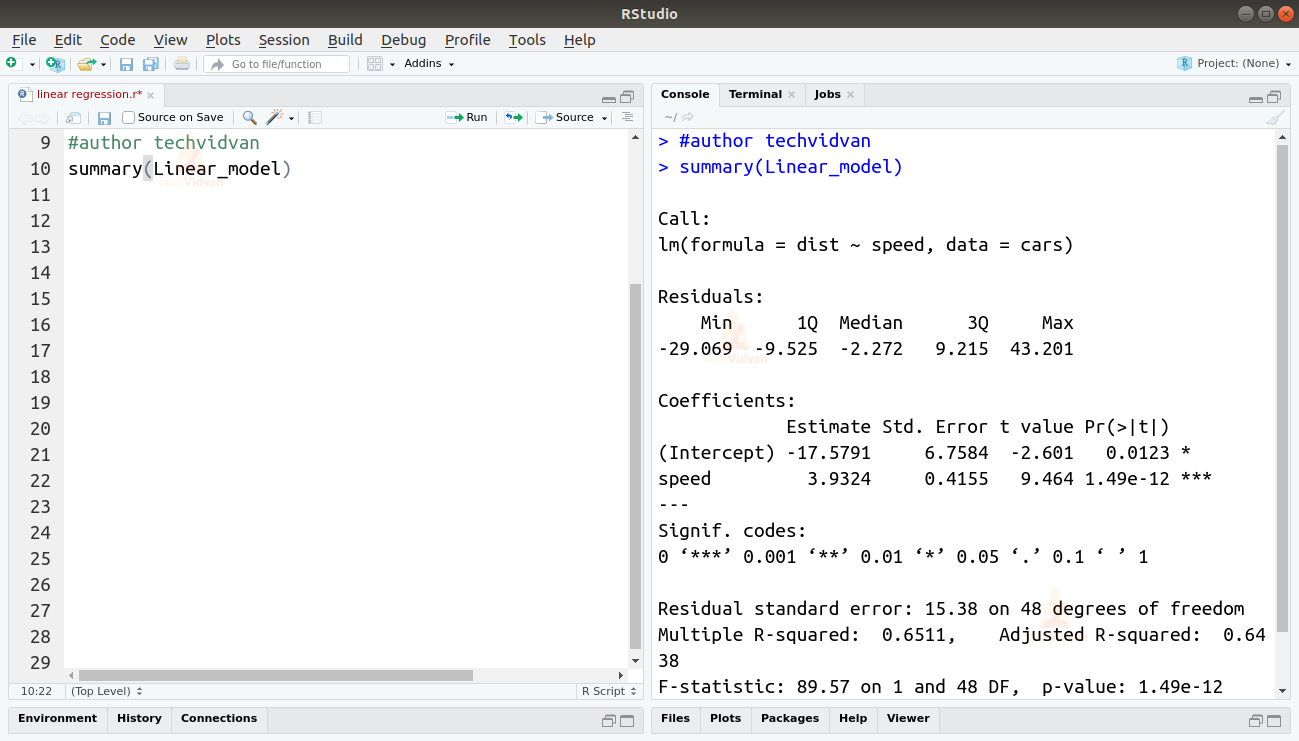
A summary() függvény néhány fontos mérőszámot ad, amelyek segítségével diagnosztizálhatjuk a modell illeszkedését. A p-érték egy fontos mérőszáma a modell illeszkedésének jóságának. Egy modellről azt mondjuk, hogy nem illeszkedik, ha a p-érték nagyobb, mint egy előre meghatározott statisztikai szignifikancia szint, amely ideális esetben 0,05.

Az összegzés a t-értéket is megadja nekünk. Minél nagyobb a t-érték, annál jobban illeszkedik a modell.
Az AIC() és a BIC() függvények segítségével meg tudjuk találni az AIC és a BIC értékét is.

AIC(Linear_model)BIC(Linear_model)

Kimenet

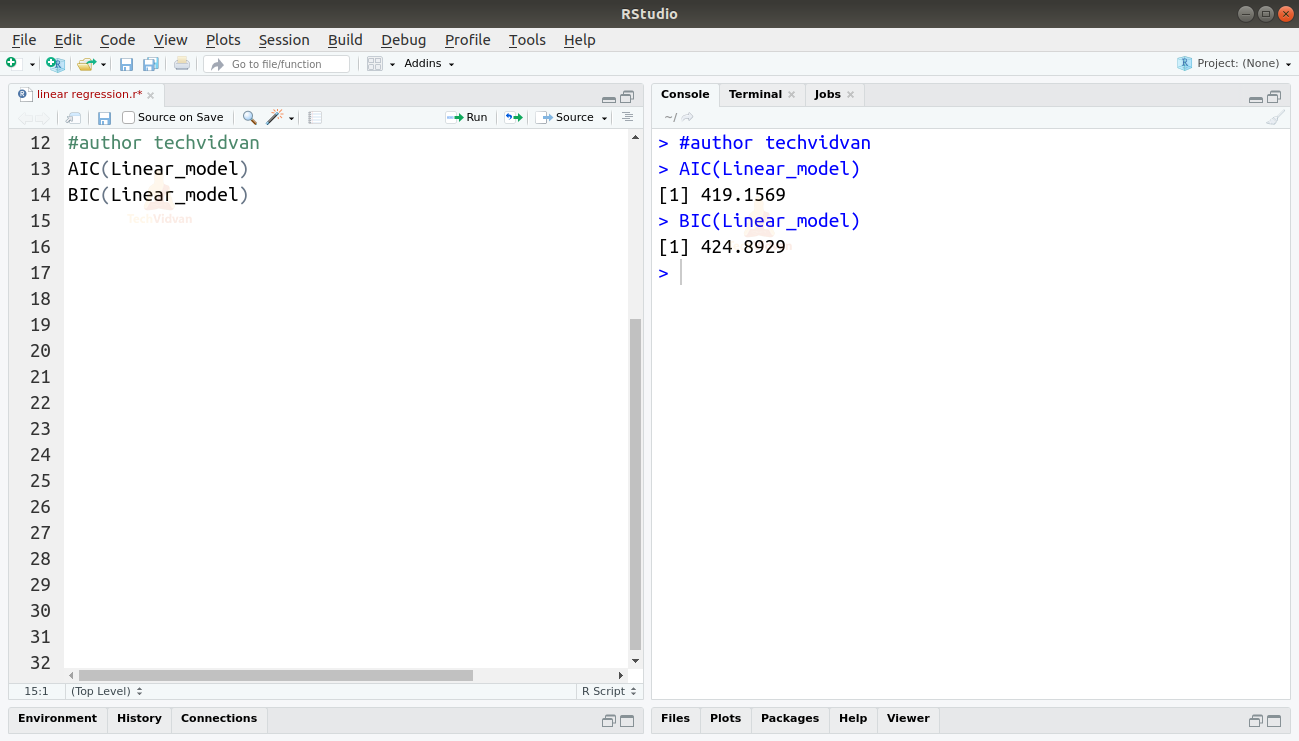
A legkisebb AIC és BIC pontszámot eredményező modell a legelőnyösebb.

Összefoglaló

A TechVidvan R oktatósorozatának ebben a fejezetében a lineáris regresszióról tanultunk. Megismertük az egyszerű lineáris regressziót és a többszörös lineáris regressziót. Ezután különböző mérőszámokat tanulmányoztunk a modell minőségének vagy pontosságának értékelésére, mint például az R2, a korrigált R2, a standard hiba, az F-statisztika, az AIC és a BIC. Ezután megtanultuk, hogyan kell a lineáris regressziót R-ben megvalósítani, majd ellenőriztük a modell illeszkedésének minőségét R-ben.

Megosztja értékelését a Google-on, ha tetszett a Lineáris regresszió oktatóanyag.