Galois elmélete a nem-matematikusoknak

Hogy egy tinédzser feltalált egy új matematikai ágat, hogy megoldjon egy régóta nyitott kérdést az egyenletekről

Azt talán tudod, hogy egy 2. fokú egyenlet megoldásához, ax²+bx+c = 0, a kvadratikus képletet használjuk.

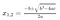
Léteznek hasonló képletek a 3. és 4. fokú egyenletekhez, de rejtélyes módon hiányoznak az 5. vagy magasabb fokúakhoz. Pontosabban úgy tűnik, hogy a kvintikus (5. fokú egyenlet) vagy magasabb fokú egyenletek megoldásait nem tudjuk megkonstruálni csak összeadás, kivonás, szorzás, osztás és gyökök (négyzetgyök, kockagyök stb.) segítségével. Miért van ez, mi olyan különleges az 5-ös számban? Ezek a kérdések kísértették a fiatal francia Evariste Galois-t az 1800-as évek elején, és aznap este, mielőtt halálosan megsebesült egy párbajban, leírta egy új matematikai objektum, az úgynevezett “csoport” elméletét, amely meglepően elegáns módon oldja meg a kérdést.

Galois-t párbajban lelőtték. Kép a Wikimédiáról.

Így csinálta.

A különböző egyenletek gyökhalmazai különböző bonyolultságúak. Egyes halmazok annyira összetettek, hogy nem lehet őket csak egyszerű objektumokkal, például gyökökkel kifejezni. De hogyan mérjük a gyökök összetettségét, ha nem is tudjuk kiszámítani őket, és milyen összetettségi mércét használjunk?

A gyökök szimmetriája és a szimmetria

A válasz a gyökök szimmetriájában rejlik.

A gyökök szimmetriája, kérdezheted, mi köze van ennek bármihez is? Mit jelent egyáltalán?

Tegyük fel két egyenlet gyökeit, és lássuk, hogy van-e értelme:

A bal oldali egyenletről azt mondják, hogy kevésbé szimmetrikus, mint a jobb oldali. Ez meglepő lehet, mert a köznyelvben a szimmetrikus szót általában akkor használjuk, ha a tárgyat tükrözni vagy elforgatni lehet anélkül, hogy a kinézete megváltozna. Ebben az értelemben a bal oldali kép szimmetrikusabbnak tűnik.

Például: A csillag szimmetrikusabb, mint a szív, mert a tükrözés mellett el is lehet forgatni.

De a mi esetünkben a szimmetriákat általánosabban fogjuk vizsgálni. Nem korlátozzuk magunkat csak a tükrözésekre és forgatásokra, minden olyan függvény, amely úgy alakítja át az objektumot, hogy közben nem változtatja meg a kinézetét, tisztességes játék. A gyökök esetében ez azt jelenti, hogy minden olyan függvény érvényes, amely a gyököket bármilyen módon felcseréli (átváltoztatja). Több függvény azt jelenti, hogy szimmetrikusabb.

Kiderült, hogy a megfelelő esetben az összes gyököt bármilyen elképzelhető sorrendben permutáló függvény létezik, akár 5!=120 is, tehát erősen szimmetrikus. De a bal esetben, ha az i↔-i transzformációval felcseréljük az r₂↔r₄-t, akkor szükségszerűen felcseréljük az r₁↔r₅-t is. Ez korlátoz bennünket, és így nem lehetséges minden elképzelhető permutáció. Ez kevésbé szimmetrikus.

A gyököket permetező függvényeket “automorfizmusoknak” nevezzük, és ha ezeket az automorfizmusokat csoportosítjuk, akkor egy úgynevezett “csoportot” kapunk (az automorfizmusok és csoportok jobb definícióira később még visszatérek).

Ez azt jelenti, hogy a gyökök szimmetriáit reprezentáló csoport a megfelelő esetben nagyobb és összetettebb. Sőt, a jobb esetben a csoport annyira összetett, hogy a gyökök nem írhatók le gyökökkel.

Honnan tudjuk, hogy egy csoport mennyire összetett? Ahhoz, hogy ezt megértsük, egy kicsit több elméletre van szükségünk.

A kvintikus mérete

Először is nézzük meg egy csoport méretét. Honnan tudom, hogy vannak olyan kvintikumok, amelyeknek 5! nagy a csoportja?

Egy általános kvintikus általában így néz ki:

x⁵+ax⁴+bx³+cx²+dx+e=0

De ha “gyökérközpontúbb” megközelítést alkalmazunk, akkor mondhatjuk, hogy így néz ki:

(x-r₁)(x-r₂)(x-r₃)(x-r₄)(x-r₅)=
x⁵-(r₁+r₂+r₃+r₄+r₅)x⁴+
(r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅)x³…- r₁r₂r₃r₄r₅=0

Ez azt jelenti, hogy az első egyenletben az a,b,c,d,e konstansokat a gyökök szimmetrikus kombinációjával helyettesítjük:

r₁+r₂+r₃+r₄+r₅=a
r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅=b
(c és d a rövidség kedvéért elhagyva)
r₁r₂r₃r₄r₅ = e

Minden tagot részletesen megvizsgálva, rájövünk, hogy a gyökök felcserélése nem befolyásolja az egyenletet (próbáljuk ki például a fenti b esetében). Ez bármilyen fokú polinomra igaz. Mivel az összes gyök felcserélhető, levonhatjuk a következtetést, hogy ennek az általános kvintikusnak a szimmetriacsoportja valójában az összes permutáció, más néven S₅ (az 5-ös rendű szimmetrikus csoport).

Mezők és automorfizmusok

Most egy kicsit kibővítjük az automorfizmusok definícióját, mivel ezek többről szólnak, mint a gyököket permutáló függvényekről. Ennek során be kell vezetnünk valamit, amit “mezőknek” nevezünk. Azt mondjátok, miért akarjuk ezt megtenni? Azért, mert míg a gyökökkel és azok permutációival dolgozni szórakoztató, addig a mezőkkel és azok automorfizmusaival kicsit egyszerűbb dolgozni. Pontosan ugyanazokról a függvényekről van szó, ne aggódj, csak másképp nézzük őket.

Szóval, ha az egyenlet mondjuk x²-2=0, ahelyett, hogy a gyökökkel dolgoznánk, r₁=√2, r₂=-√2, bevezetjük a Q(√2) mezőt. Ez az összes Q racionális számot jelenti egy hozzáadott √2-vel. Az √2-t “mezőbővítésnek” nevezzük. Ez így néz ki: a+b√2 a,b∈Q. Ahhoz, hogy le tudjuk írni az egyenlet gyökét, szükségünk van a Q(√2) mezőre. Minden mezőbővítményre (és más matematikai objektumokra is) van egy csomó σₙ függvényünk, amelyek egy számot ugyanabban a mezőben egy másik egyedi számra küldenek, és a σ(a+b)=σ(a)+σ(b) és σ(ab)=σ(a)σ(b) feltételt követik. σ a bővítmény függvénye, és nem érinti a mögöttes Q mezőt. Ezeket a függvényeket automorfizmusoknak nevezzük. Mellesleg ezek is permutes a gyökök. Ez azért van, mert az r gyökér esetében:

r⁵+ar⁴+br³+cr²+dr+e=0⟹
σ(r⁵+ar⁴+br³+cr²+dr+e)=σ(0)⟹
σ(r)⁵+aσ(r)⁴+bσ(r)³+cσ(r)²+dσ(r)+e=0 (mivel σ nem érinti Q-t (ahol a, b, c, d,e él))

Ez azt jelenti, hogy σ(r) is az egyenlet megoldása. És mivel:

σ(r₁)-σ(r₂)=σ(r₁)+σ(-1)σ(r₂)=σ(r₁-r₂)≠0

a gyökök különbözőek, tehát 5 gyökünk van, ami az eredeti 5 lehet. Így σ-nak kell permuttálnia a gyököket.

Ez természetesen bármilyen fokú egyenletre működik.

Ezért:

Megvan az egyenletünk.
Ez az egyenlet rendelkezik egy mezővel, amely tartalmazhat egy néhány gyökből álló kiterjesztést
Ez a kiterjesztés rendelkezik egy csoporttal, amely az összes automorfizmusának a gyűjteménye.

Két 3. fokú példa

Egyenlet:

A gyökök (1,√2,-√2,-√2) (ezt magad is ellenőrizheted, ha csak bedugod őket), tehát a mezőnek Q(√2)

Az összes olyan módot leírjuk, amire gondolni tudunk, hogy a gyököket permuttáljuk (az e identitáspermutációt jelent, az nem csinál semmit):

(e)
(√2↔-√2)
(1↔√2)
(1↔-√2)
(√2→-√2 és 1→√2)
(√2↔-√2 és 1↔-√2)

Vizsgáljunk meg egyet: Legyen (√2↔-√2) σ₁:

σ₁(√2+-√2)=σ₁(0)=0=σ₁(√2)+σ₁(-√2)
σ₁((√2)(-√2))=σ₁(-2)=-2=σ₁(√2)σ₁(-√2)

Szóval eddig jó. Még egy.

Legyen (1↔√2) σ₂:

σ₂(√2+-√2)=σ₂(0)=0 ≠ σ₂(√2)+σ₂(-√2)=1+-√2
σ₂((√2)(-√2))=2 ≠ σ₂(√2)σ₂(-√2)=1(-√2)

Látszólag σ₂ nem automorfizmus, így el kell vetnünk. A többi σ is hasonló problémákba ütközik, csak az e és a σ₁ marad. Ezt nevezzük C₂ ciklikus csoportnak, mivel csak egy körben (ebben az esetben egy nagyon kis körben) tudunk permuteálni.

2. példa

Egyenlet:

A gyökök

so a mezőnek

a rövidség kedvéért ζ-t használva. Ez így néz ki:

Egy kicsit játszadozhatunk a gyökpermutációkkal, és hamar észrevesszük, hogy ebben az esetben ezek mind automorfizmusok. Tehát 3! automorfizmus van, ami az összes gyökpermutáció, tehát a csoportnak S₃-nak kell lennie.

A fenti képpel kapcsolatban még egy vicces dolog, hogy úgy néz ki, mint egy egyenlő oldalú háromszög, és hogy az automorfizmusok pontosan megfelelnek a háromszög forgatásának és tükrözésének. Ha az automorfizmusok ilyen módon megfelelnek egy szabályos sokszög szimmetriáinak, akkor a csoportot “diéderes csoportnak” nevezzük. Ebben az esetben D₃. Általában az összes permutáció Sₙ csoportja nem azonos a Dₙ diéderes csoporttal, de n=3 esetén igen.

Groups

Ez egy jó helynek tűnik arra, hogy átmenjünk egy kicsit hosszabb beszélgetésbe a csoportokról. A csoportok tehát a gyökök permutációinak gyűjteményeiként indultak, de tekinthetjük automorfizmusok, vagy szimmetrikus geometriai objektumok forgatásainak és tükrözéseinek gyűjteményének is. Minden olyan függvénygyűjtemény, amely egy objektumot úgy változtat meg, hogy az ugyanúgy nézzen ki, csoportnak tekinthető. De tulajdonképpen magukat a transzformációkat is megnézhetjük anélkül, hogy foglalkoznánk azzal a szimmetrikus objektummal, amelyre hatnak. Ugyanúgy, ahogy számoláskor nem foglalkozunk az almakupacokkal, hanem egyszerűen követjük a szabályokat, hasonlóképpen meghatározhatunk néhány szabályt, amelyeket egy csoport transzformációi követnek, és felhasználhatjuk őket.

A szabályok valahogy így néznek ki:

Ha először egy transzformációt végzünk, majd egy másikat, akkor egy harmadik transzformációt kapunk, amely még mindig a csoportban van. Például a C₄ csoport az összes olyan forgatás csoportja, amelyet egy négyzeten elvégezhetünk. Ha a 90∘-t forgat, b 180∘-t forgat, és c 270∘-t forgat, akkor a∗b=c. Ahol a ∗ azt jelenti, hogy először b, majd a, amit általában szorzásnak neveznek, mivel (valahogy) hasonlít a számok szorzásához. A fenti szabály szerint c-nek a csoportban kell lennie. Ezt nevezzük zártságnak.

Meg kell lennie egy azonossági elemnek (e), amely egyáltalán nem csinál semmit.

Minden elemhez kell lennie egy fordítottjának.

Most már vizsgálhatjuk a különböző csoportok tulajdonságait anélkül, hogy a gyökökkel vagy a sokszögekkel kellene foglalkoznunk.

A csoportok vizualizálása

A csoportok vizualizálásának két szórakoztató módja:

Cayley-táblák

A fenti kép egy egyenlő oldalú háromszög, a D₃ csoport Caylay-táblája. Ez a csoport összes eleme és az, hogy milyen elemeket kapunk, ha megszorozzuk őket. Például, ha először 120∘ elforgatást végzünk (r), majd ugyanezt az elforgatást még egyszer, akkor 240∘ elforgatást kapunk rr=r², ahogy a táblázatban is látható. Ha 120∘ forgás-flip rf-et és egy r-t csinálunk, akkor csak egy flip-et kapunk. Vegyük észre, hogy az f és r elemek nem ingadoznak. Az olyan csoportot, ahol az elemek ingadoznak, abéliumos csoportnak nevezzük.

Ez a táblázat még mindig nagyon szimmetrikus, de ennek nem kell így lennie. Az elemek bármilyen, a szabályokat követő összevisszasága érvényes.

Caylay-gráf

A fenti a D₃ Caylay-gráf. Itt az elemek úgy vannak ábrázolva, hogy megmutatják, hogyan jutunk el egyik elemtől a másikig, ahol az élek a műveleteket jelentik. Ebben az esetben egy 120∘ forgatásra és egy flipre van szükség, ezeket (r és f) a csoport generátorainak is nevezik, mert az azonossági elemből kiindulva velük lehet az egész csoportot generálni.

A csoportok felhasználása

A csoportok általában mindenütt hasznosak, ahol szimmetria van. Például a tapétacsoportokat szimmetrikus tapéták leírására használják. Vannak olyan háttérképek, amelyeket 180∘-kal elforgathatunk, és vannak olyanok, amelyeket tükrözhetünk, és vannak olyanok, ahol mindkettőt megtehetjük, és így tovább. Kiderült, hogy csak 17 van belőlük, így ez egy ügyes módja a háttérképek osztályozásának.

A fenti háttérképek mindkettő egy p6m nevű csoportba tartozik.

A csoportok másik, meglepőbb felhasználása a fizikában van. Úgy tűnik, mintha a természet törvényei bizonyos szimmetriákat követnének. Például, ha átalakítjuk Newtons második törvényét F=ma, 10 perccel a jövőbe nézve még mindig ugyanaz marad. Az, hogy a természeti törvények nem változnak egyik napról a másikra, arra látszik utalni, hogy szimmetrikusak az idő-transzformáció tekintetében. Nem változnak egyik helyről a másikra sem, tehát a térbeli átalakulások is megengedettek. Mivel az idő és a tér tetszőlegesen kis vagy nagy darabokban átalakítható, az ezeket leíró csoportok, a Lie-csoportok, végtelen számú elemet tartalmaznak.

Érdekes módon kiderül, hogy ezek a szimmetriák mind egy-egy megőrzési törvényhez kapcsolódnak. Az időszimmetria az energia megőrzését vonja maga után, a térszimmetria az impulzusmegőrzést, a szögszimmetria (a természet minden szögből ugyanúgy néz ki) az impulzusmegőrzést és így tovább. Ezt Emmy Noether úgy mutatta meg, hogy a szimmetriákat egyszerűen összekapcsolta a legkisebb hatás elvével, egy természeti törvénnyel, amely kimondja, hogy a természet hajlamos “a legrövidebb utat választani”.

Én érdekesnek találom, hogy a természet bonyolultsága és látszólagos káosza mennyire megmagyarázható olyan intuitív fogalmakkal, mint “a természeti törvények nem változnak napról napra” és “a természet hajlamos a legrövidebb utat választani”.

Vissza a mezőkhöz

Vége az intermezzónak, hol is tartottunk? Igaz, az x³-3=0-ról és annak gyökeiről és mezőiről beszéltünk.

Az egyenlet mezője Q(³√2, ζ), és természetes lenne azt gondolni, hogy ez így néz ki: a+b³√2+cζ, de ez tévedés. Ennek az az oka, hogy azt szeretnénk, ha a mezőnk “zárt” lenne. Azaz, ha két elemet összeadunk vagy megszorozunk a mezőben, akkor a mezőben akarunk maradni. Tehát például ³√2 és ζ mindkettő benne van a fenti mezőben, de ³√2ζ nem.

Almezők és alcsoportok

A fenti 3. fokú példáinkat nézve

van.

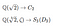
A második mező és csoport látszólag összetettebb, mint az első mező és csoport. Ezt úgy is kitalálhatjuk, hogy egyszerűen megszámoljuk a kifejezések számát a mező esetében, vagy az automorfizmusok számát a csoport esetében. De úgy tűnik, hogy a puszta számolás nem igazán ragadja meg azt, hogy mit jelent komplexnek lenni. Vegyük például a C₁₂ csoportot. Rengeteg elem, de csak a gyököket forgatja, így nem tűnik igazán komplexnek. A megfelelő mező a Q(e^π/6). Ez tartalmazni fogja e^π/6,e^2π/6… de ismét nem túl bonyolult.

Az, hogy mennyire bonyolult egy csoport, kulcsfontosságú lesz annak megértéséhez, hogy miért nem lehet egyes gyököket csak gyökökkel leírni, ne feledjük.

A komplexitás jobb megítéléséhez bevezetjük az “almező” és az “alcsoport” fogalmát. Almezőnek nevezzük azt, amikor néhány kifejezést eltávolítunk, de még mindig zárt mezőt kapunk. Hasonlóképpen, egy alcsoport az, amikor eltávolítunk néhány automorfizmust, de még mindig van egy zárt csoportunk.

Az első esetben Q(√2), az egyetlen dolog, amit tehetünk, hogy eltávolítjuk a √2-t a mezőben és a két automorfizmus egyikét a csoportban (nem tudjuk eltávolítani (e) és még mindig van egy csoportunk).

A második esetben Q(³√2, ζ), ez egy kicsit bonyolultabbá válik. Az almezőket/csoportokat kézzel is le lehet desztillálni úgy, hogy csak egyesével távolítjuk el az elemeket, és megnézzük, hogy az így kapott mező/csoport zárt-e. Egy idő után erre jutunk:

A Q(⁴√2, i) mezőnek D₄ permutációs csoportja van (ugyanolyan, mint a négyzet). Nézzük meg D₄-t és alcsoportjait.

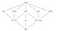
Az alcsoportrács ezen a képen fejjel lefelé van, a D₄ alul van, erre hamarosan rátérek, de először nézzük meg az alcsoportokkal ellentétes alcsoportokat. Q(⁴√2, i) 5 nagy almezővel és 3 kis alalcsoporttal rendelkezik, de D₄ csak 3 nagy alcsoporttal és 5 kisebb alalcsoporttal rendelkezik.

Úgy tűnik, mintha nem lenne elég nagy csoport az 5 nagy alcsoport permuttálásához. Ha az alcsoportokkal és az almezőkkel játszanál, akkor végül arra a következtetésre jutnál, hogy az alcsoportok valójában nem az almezőket permuteálják, hanem mindent, ami nem az almezőkben van, hogy “rögzítik” vagy nem érintik az almezőket.

Így például (f) fixálja Q(⁴√2) és (r², f) fixálja Q(√2).

Miért van ez így, és nem fordítva, ahogy először gondoltuk?

Nem tudom ezt intuitív módon megmagyarázni, én úgy látom, hogy empirikusan felfedeztük, és most megpróbálhatjuk bizonyítani. A bizonyítás valahogy így megy:

Kézzelfogható Galois-elmélet alaptétele bizonyítási vázlat

Meg akarjuk mutatni, hogy ha az alcsoportrácsot fejjel lefelé fordítjuk, akkor egy-egy megfeleltetést kapunk az almezőráccsal, ahol a mezők a csoportok fix mezői.

Először is szeretném kiemelni, hogy ésszerű (mondhatni), hogy ez így van. Az alsó csoportnál van az összes automorfizmusunk, amelyek természetesen mindent mozgatnak, kivéve Q-t (Q-t fixálja), a felsőnél pedig csak az e-automorfizmus van, amely semmit sem mozgat (mindent fixál).

Ha az alsó csoportnál kezdjük és eltávolítunk néhány automorfizmust, akkor az eltávolított automorfizmusok már nem mozognak a mező egy kis része körül, és így a mezőnek ezt a részét fixálják. Ahogy egyre több automorfizmust távolítunk el, a mező egyre nagyobb része marad érintetlen, és így egyre nagyobb lesz a rögzített mezőnk.

Hogy egy kicsit szigorúbbak legyünk, össze kell tudnunk hasonlítani a csoport és a mező méretét. A csoport mérete természetesen a benne lévő automorfizmusok száma. A mező mérete a tagok száma. Ez a kettő történetesen ugyanaz, de miért van ez így?

Kuotiens

Most megnézhetjük a kvintikus S₅ alcsoportrácsát, és láthatjuk, hogy valóban elég bonyolultnak tűnik. De ahhoz, hogy ezt összekapcsoljuk a gyökökkel, szükségünk van egy olyan módszerre, amellyel a csoportok és alcsoportjai közötti komplexitást elemezhetjük. Vagyis: Mennyivel komplexebb a D₄, mint például a C₄? Ehhez bevezetjük a “hányados” fogalmát. A hányados alapvetően csoportosztás. Hogyan működik ez?

A közönséges osztásnál valami ilyesmit csinálunk: Ha 15 almát 5 személyre akarunk osztani, akkor az alma-halmazban lévő almákat 5 egyenlő halomba csoportosítjuk, és minden halom megfelel egy személynek a személy-halmazban. A 15/5 kérdésre a válasz 3, az egyik halom, bármelyik halom megteszi, hiszen egyenlőek.

A csoportokra osztásnál is hasonló történik. Ha D₄-t osztjuk C₄-vel, akkor D₄ 8 elemét 4 egyenlő csoportba csoportosítjuk, C₄ minden eleméhez egyet. Hogyan tesszük egyenlővé a csoportokat? Nem mintha az elemek mind egyforma almák lennének. Ezek például nagyon különböző automorfizmusok lehetnek. Nos, a kvóták pontosan emiatt nem mindig lehetségesek. De néha egy csoportot fel lehet osztani “kozettekre”. Tegyük fel, hogy D₄-t 4 egyenlő részre osztjuk, mindegyikben 2 elemmel. Ha szerencsénk van, akkor 4 olyan elemhalmazt kapunk, ahol a két elem közötti kapcsolat minden halmazban azonos. Ehhez az eredeti csoportnak nagyfokú önhasonlóságot kell mutatnia. Hogy ezt lássuk, nézzük meg a D₄ Cayley-gráfját.

Amint látható, itt valóban nagyfokú önhasonlóság van. A bal felső, a jobb felső, a bal alsó és a jobb alsó sarok mind ugyanúgy néz ki. Ez a mi kozettünk.

A D₄/C₄ tehát alapvetően az egyik ilyen kozett, ami a C₂. Ebből következően: D₄/C₄=C₂.

Most, a kvóták bevezetésével tulajdonképpen van egy fogalmunk arról, hogyan építhetünk csoportokat az alapoktól kezdve. Ahogyan a 21 a 3-ból és a 7-ből áll, úgy állnak a csoportok is az alcsoportjaikból. És ahogyan egy szám alkotóit is megkaphatjuk osztással, 21/7=3, úgy egy csoport alkotóit is megkaphatjuk a hányadossal. Mivel D₄/C₄=C₂, ez azt jelenti, hogy ha van egy C₄ csoportunk, akkor azt meg kell szoroznunk C₂-val, hogy megkapjuk a D₄ értéket. Mivel a mezők és a csoportok között megfeleltetés van, ez szerepet fog játszani abban, hogy hogyan konstruáljuk a mezőket.