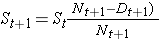Estamos frequentemente interessados em avaliar se existem diferenças na sobrevivência (ou incidência acumulada de eventos) entre os diferentes grupos de participantes. Por exemplo, em um estudo clínico com um resultado de sobrevivência, podemos estar interessados em comparar a sobrevivência entre participantes recebendo um novo medicamento em comparação com um placebo (ou terapia padrão). Em um estudo observacional, podemos estar interessados em comparar sobrevivência entre homens e mulheres, ou entre participantes com e sem um fator de risco particular (por exemplo, hipertensão ou diabetes). Existem vários testes disponíveis para comparar a sobrevivência entre grupos independentes.

O Log Rank Test

O log rank test é um teste popular para testar a hipótese nula de não haver diferença na sobrevivência entre dois ou mais grupos independentes. O teste compara toda a experiência de sobrevivência entre grupos e pode ser pensado como um teste para verificar se as curvas de sobrevivência são idênticas (sobrepostas) ou não. As curvas de sobrevivência são estimadas para cada grupo, consideradas separadamente, usando o método de Kaplan-Meier e comparadas estatisticamente usando o teste de log rank. É importante notar que existem várias variações da estatística do teste de log rank que são implementadas por vários pacotes de computação estatística (por exemplo, SAS, R 4,6). Apresentamos aqui uma versão que está estreitamente ligada à estatística do teste de qui-quadrado e que compara com o número esperado de eventos em cada ponto do período de acompanhamento.

Exemplo:

Um pequeno ensaio clínico é executado para comparar dois tratamentos combinados em pacientes com câncer gástrico avançado. Vinte participantes com câncer gástrico estágio IV que consentem em participar do estudo são designados aleatoriamente para receber quimioterapia antes da cirurgia ou quimioterapia após a cirurgia. O resultado primário é a morte e os participantes são acompanhados por até 48 meses (4 anos) após a inscrição no estudo. As experiências dos participantes em cada braço do estudo são mostradas abaixo.

>

>

>

>

>

>>

Chemoterapia antes da cirurgia			Chemoterapia após a cirurgia
Mês de Morte	Mês do Último Contato		Mês da Morte	> Mês do Último Contato
8	8		33	48
12	32		28	48
26	20		41	25
14	40			37
21				48
27				25
				> 43

Seis participantes no grupo de quimioterapia antes da cirurgia morrem no decurso do seguimento…em comparação com três participantes do grupo de quimioterapia após a cirurgia. Outros participantes de cada grupo são acompanhados durante vários meses, alguns até ao final do estudo aos 48 meses (no grupo de quimioterapia após a cirurgia). Usando os procedimentos descritos acima, primeiro construímos tabelas de vida para cada grupo de tratamento usando a abordagem Kaplan-Meier.

Tabela de vida para o grupo que recebe quimioterapia antes da cirurgia

Tempo, Meses	Número em risco Nt	Número de mortes Dt	Número Censurado Ct	Probabilidade de sobrevivência
0	10			1
8	10	1	1	0.900
12	8	1		0.788
14	7	1		0.675
20	6		1	0.675
21	5	1		0.540
26	4	1		0.405
27	3	1		0.270
32	2		1	0.270
40	1		1	0.270 >

Tabela de Vida para Grupos que Recebem Quimioterapia Pós-Cirurgia

Tempo, Meses	Número em risco Nt	Número de mortes Dt	Número Censurado Ct	Probabilidade de sobrevivência
0	10			1
25	10		2	1.000
28	8	1		0.875
33	7	1		0.750
37	6		1	0.750
41	5	1		0.600
43	4		1	0.600
48	3		3	0.600

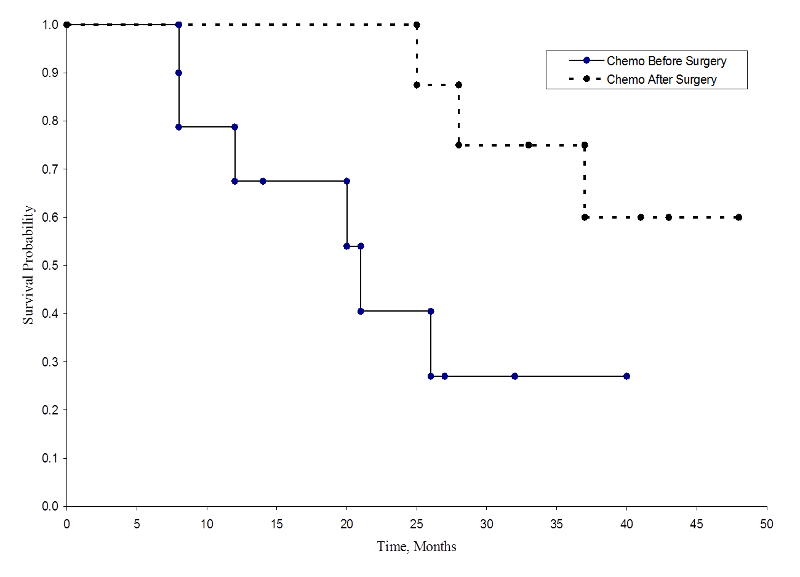
As duas curvas de sobrevivência são mostradas abaixo.

Sobrevivência em Cada Grupo de Tratamento

>

As probabilidades de sobrevivência para o grupo de quimioterapia após a cirurgia são maiores do que as probabilidades de sobrevivência para o grupo de quimioterapia antes da cirurgia, sugerindo um benefício de sobrevivência. Entretanto, estas curvas de sobrevivência são estimadas a partir de pequenas amostras. Para comparar a sobrevida entre grupos podemos usar o teste de log rank. A hipótese nula é que não há diferença na sobrevivência entre os dois grupos ou que não há diferença entre as populações na probabilidade de morte em qualquer ponto. O teste de log rank é um teste não paramétrico e não faz suposições sobre as distribuições de sobrevivência. Em essência, o teste de log rank compara o número de eventos observados em cada grupo com o que seria esperado se a hipótese nula fosse verdadeira (i.e, se as curvas de sobrevivência fossem idênticas).

H0: As duas curvas de sobrevivência são idênticas (ou S1t = S2t) versus H1: As duas curvas de sobrevivência não são idênticas (ou S1t ≠ S2t, em qualquer momento t) (α=0,05).

A estatística de log rank é distribuída aproximadamente como uma estatística do teste do qui-quadrado. Há várias formas de estatística do teste, e elas variam em termos de como são computadas. Usamos o seguinte:

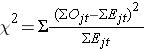
onde ΣOjt representa a soma do número de eventos observados no grupo j ao longo do tempo (por exemplo, j=1,2) e ΣEjt representa a soma do número esperado de eventos no grupo j ao longo do tempo.

As somas dos números observados e esperados de eventos são computadas para cada tempo de evento e somadas para cada grupo de comparação. A estatística do log rank tem graus de liberdade iguais a k-1, onde k representa o número de grupos de comparação. Neste exemplo, k=2 então a estatística do teste tem 1 grau de liberdade.

Para calcular a estatística do teste precisamos do número de eventos observados e esperados em cada tempo de evento. O número de eventos observados é da amostra e o número esperado de eventos é calculado assumindo que a hipótese nula é verdadeira (ou seja, que as curvas de sobrevivência são idênticas).

Para gerar o número esperado de eventos organizamos os dados em uma tabela de vida com linhas representando cada tempo de evento, independentemente do grupo em que o evento ocorreu. Também mantemos o controle da atribuição de grupos. Estimamos então a proporção de eventos que ocorrem em cada momento (Ot/Nt) usando dados de ambos os grupos combinados sob a hipótese de não haver diferença na sobrevivência (ou seja, assumindo que a hipótese nula é verdadeira). Multiplicamos essas estimativas pelo número de participantes em risco naquele momento em cada um dos grupos de comparação (N1t e N2t para os grupos 1 e 2 respectivamente).

Especificamente, calculamos para cada tempo de evento t, o número em risco em cada grupo, Njt (por exemplo, onde j indica o grupo, j=1, 2) e o número de eventos (mortes), Ojt ,em cada grupo. A tabela abaixo contém as informações necessárias para realizar o teste de classificação dos registros para comparar as curvas de sobrevivência acima. O grupo 1 representa o grupo de quimioterapia antes da cirurgia e o grupo 2 representa o grupo de quimioterapia após a cirurgia.

Dados para o teste de log rank para comparar as curvas de sobrevivência

Tempo, Meses	Número em risco no grupo 1 N1t	Número em risco no grupo 2 N2t	Número de eventos (Mortes) no grupo 1 O1t	Número de Eventos (Mortes) no Grupo 2 O2t
8	10	10	1	> 0
12	8	10	1	0
14	7	10	1	0
21	5	10	1	0
26	4	8	1	0
27	3	8	1	0
28	2	8	0	1
33	1	7	0	1
41	0	5	0	1

A seguir totalizamos o número em risco, Nt = N1t+N2t, em cada momento do evento e o número de eventos observados (mortes), Ot = O1t+O2t, em cada momento do evento. Em seguida, calculamos o número esperado de eventos em cada grupo. O número esperado de eventos é calculado em cada momento de evento da seguinte forma:

E1t = N1t*(Ot/Nt) para o grupo 1 e E2t = N2t*(Ot/Nt) para o grupo 2. Os cálculos são mostrados na tabela abaixo.

Números esperados de eventos em cada grupo

Tempo, Meses	Número em risco no grupo 1 N1t	Número em risco no grupo 2 N2t	Número total em risco Nt	Número de Eventos no Grupo 1 O1t	Número de Eventos no Grupo 2 O2t	Número Total de Eventos Ot	Número de Eventos previsto em Grupo 1 E1t = N1t*(Ot/Nt)	Número de Eventos previsto em Grupo 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000

A seguir somamos os números de eventos observados em cada grupo (∑O1t e ΣO2t) e os números de eventos esperados em cada grupo (ΣE1t e ΣE2t) ao longo do tempo. Estes são mostrados na linha inferior da próxima tabela abaixo.

Números Totais Observados e Esperados de Observados em cada Grupo

Tempo, Meses	Número em risco no grupo 1 N1t	Número em risco no grupo 2 N2t	Número total em risco Nt	Número de Eventos no Grupo 1 O1t	Número de Eventos no Grupo 2 O2t	Número Total de Eventos Ot	Número de Eventos previsto em Grupo 1 E1t = N1t*(Ot/Nt)	Número de Eventos previsto em Grupo 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000
				6	3		2.620	6.380

Agora podemos calcular a estatística do teste:

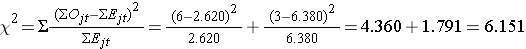
A estatística do teste é distribuída aproximadamente como qui-quadrado com 1 grau de liberdade. Assim, o valor crítico para o teste pode ser encontrado na tabela de Valores Críticos da distribuição Χ2.

Para este teste a regra de decisão é Rejeitar H0 se Χ2 > 3.84. Observamos Χ2 = 6,151, o que excede o valor crítico de 3,84. Portanto, nós rejeitamos H0. Temos evidências significativas, α=0.05, para mostrar que as duas curvas de sobrevivência são diferentes.

Exemplo:

Um investigador deseja avaliar a eficácia de uma breve intervenção para prevenir o consumo de álcool na gravidez. Mulheres grávidas com histórico de consumo pesado de álcool são recrutadas para o estudo e aleatorizadas para receber a intervenção breve focada na abstinência de álcool ou no pré-natal padrão. O resultado do interesse é a recidiva do consumo de álcool. As mulheres são recrutadas para o estudo com aproximadamente 18 semanas de gestação e acompanhadas durante o curso da gravidez até o parto (aproximadamente 39 semanas de gestação). Os dados são mostrados abaixo e indicam se as mulheres recaem ao beber e, em caso afirmativo, o tempo da primeira bebida medido no número de semanas a partir da aleatorização. Para as mulheres que não recaem, registramos o número de semanas a partir da aleatorização que elas estão livres de álcool.

Cuidado pré-natal padrão			> Intervenção do paciente
Relapso	Não há recapso		Relapso	Não há recapso
19	20		16	21
6	19		21	15
5	17		7	18
4	14			18
				>5

A questão de interesse é se existe uma diferença de tempo de recidiva entre as mulheres atribuídas aos cuidados pré-natais padrão em comparação com as atribuídas à intervenção breve.

• Passo 1.

Estabelecer hipóteses e determinar o nível de significância.

H0: O tempo livre de recidiva é idêntico entre grupos versus

H1: O tempo livre de recidiva não é idêntico entre grupos (α=0.05)

• Passo 2.

Selecionar a estatística de teste apropriada.

A estatística do teste para o log rank test é

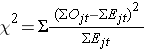
• Passo 3.

Configurar a regra de decisão.

A estatística do teste segue uma distribuição qui-quadrada, e assim encontramos o valor crítico na tabela de valores críticos para a distribuição Χ2) para df=k-1=2-1=1 e α=0.05. O valor crítico é 3,84 e a regra de decisão é rejeitar H0 se Χ2 > 3,84.

• Passo 4.

Compute a estatística do teste.

Para calcular a estatística do teste, organizamos os dados de acordo com os tempos de evento (recidiva) e determinamos o número de mulheres em risco em cada grupo de tratamento e o número de recidivas em cada tempo de recidiva observado. Na tabela a seguir, o grupo 1 representa as mulheres que recebem o pré-natal padrão e o grupo 2 representa as mulheres que recebem a intervenção breve.

Tempo, Semanas	Número em risco – Grupo 1 N1t	Número em risco – Grupo 2 N2t	Número de recaídas – Grupo 1 O1t	> Número de recaídas – Grupo 1 Grupo 2 O2t
4	8	8	1	0
5	7	8	1	0
6	6	7	1	0
7	5	7	0	1
16	4	5	0	1
19	3	2	1	0
21	0	2	0	1

A seguir totalizamos o número em risco, 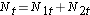, em cada momento de evento, o número de eventos observados (recaídas), 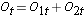, em cada momento de evento e determinar o número esperado de recaídas em cada grupo em cada momento de evento usando 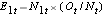e .

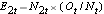Soma, então, os números de eventos observados em cada grupo (ΣO1t e ΣO2t) e os números de eventos esperados em cada grupo (ΣE1t e ΣE2t) ao longo do tempo. Os cálculos para os dados deste exemplo são mostrados abaixo.

Tempo, Semanas	Número no Grupo de Risco 1 N1t	Número no Grupo de Risco 2 N2t	Número total no Grupo de Risco Nt	Número de relapses Grupo 1 O1t	Número de relapses Grupo 2 O2t	Número total de relapses Ot	Número esperado de recaídas no grupo 1 >	Número esperado de recaídas no grupo 2
4	8	8	16	1	0	1	0.500	0.500
5	7	8	15	1	0	1	0.467	0.533
6	6	7	13	1	0	1	0.462	0.538
7	5	7	12	0	1	1	0.417	0.583
16	4	5	9	0	1	1	0.444	0.556
19	3	2	5	1	0	1	0.600	0.400
21	0	2	2	0	1	1	0.000	1.000
				4	3		2.890	4.110

Agora calculamos a estatística do teste:

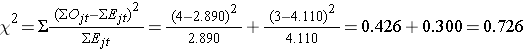
• Passo 5.

Conclusão. Não rejeite H0 porque 0,726 < 3,84. Não temos evidências estatisticamente significativas em α=0,05, para mostrar que o tempo de recidiva é diferente entre os grupos.

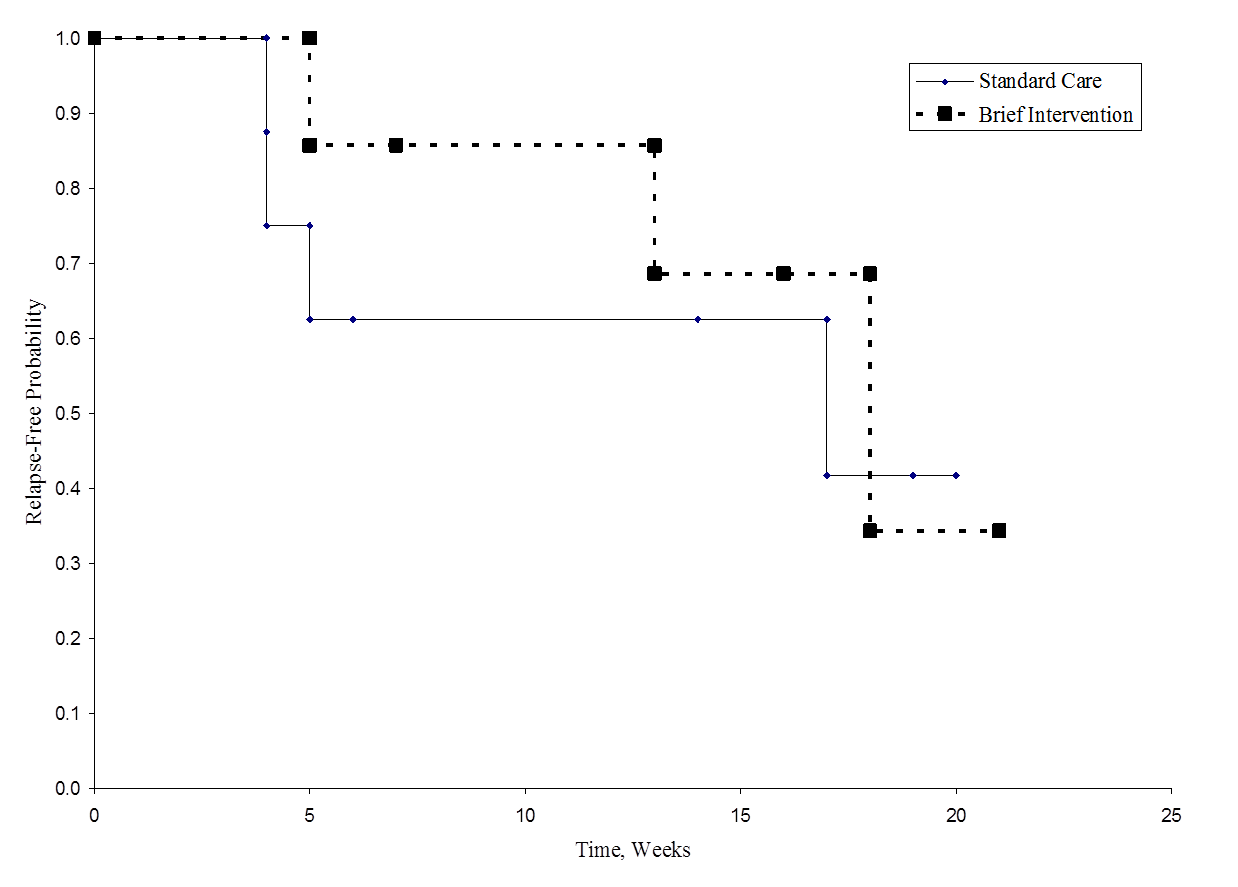
A figura abaixo mostra a sobrevivência (tempo livre de recidiva) em cada grupo. Observe que as curvas de sobrevivência não mostram muita separação, consistente com os achados não significativos no teste de hipóteses.

Tempo livre de recidiva em cada grupo

Como observado, há várias variações da estatística de classificação logarítmica. Alguns pacotes de computação estatística usam a seguinte estatística de teste para o teste de log rank para comparar dois grupos independentes:

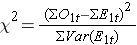
onde ΣO1t é a soma do número de eventos observados no grupo 1, e ΣE1t é a soma do número esperado de eventos no grupo 1, tomado sobre todos os tempos de eventos. O denominador é a soma das variâncias do número esperado de eventos em cada tempo de evento, que é calculado da seguinte forma:

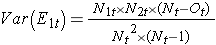
Existem outras versões da estatística do log rank, bem como outros testes para comparar funções de sobrevivência entre grupos independentes.7-9 Por exemplo, um teste popular é o teste Wilcoxon modificado que é sensível a diferenças maiores nos perigos mais cedo do que mais tarde no seguimento.10

retornar ao topo | página anterior | página seguinte