#InsideRL
Em um problema típico de Aprendizagem do Reforço (RL), há um aprendiz e um tomador de decisão chamado agente e o ambiente com o qual interage é chamado ambiente. O ambiente, em troca, fornece recompensas e um novo estado baseado nas ações do agente. Assim, no aprendizado de reforço, não ensinamos a um agente como ele deve fazer algo, mas o apresentamos com recompensas, sejam elas positivas ou negativas, baseadas em suas ações. Portanto, a nossa questão fundamental para este blog é como formulamos matematicamente qualquer problema na RL. É aqui que entra o Processo de Decisão de Markov (MDP).

Antes de respondermos à nossa pergunta raiz, ou seja Como formulamos matematicamente os problemas RL (usando o MDP), precisamos desenvolver nossa intuição sobre :
- A relação Agente-Ambiente
- A propriedade Markov
- Processo Markov e cadeias Markov
- Processo de Recompensa Markov (MRP)
- Equação Bellman
- Processo de Recompensa Markov
Grab seu café e não pare até que você esteja orgulhoso!🧐
A Relação Agente-Ambiente
Primeiro vamos olhar para algumas definições formais :
Agente : Programas de software que tomam decisões inteligentes e são os aprendizes na RL. Estes agentes interagem com o ambiente através de ações e recebem recompensas com base em suas ações.
Ambiente :É a demonstração do problema a ser resolvido. Agora, podemos ter um ambiente do mundo real ou um ambiente simulado com o qual nosso agente irá interagir.

Estado : Esta é a posição dos agentes em um determinado momento no ambiente. Assim, sempre que um agente executa uma ação, o ambiente dá ao agente uma recompensa e um novo estado onde o agente atingiu ao executar a ação.
Qualquer coisa que o agente não possa mudar arbitrariamente é considerada como parte do ambiente. Em termos simples, as ações podem ser qualquer decisão que queremos que o agente aprenda e o estado pode ser qualquer coisa que possa ser útil na escolha das ações. Nós não assumimos que tudo no ambiente é desconhecido para o agente, por exemplo, o cálculo da recompensa é considerado como parte do ambiente mesmo que o agente saiba um pouco sobre como sua recompensa é calculada em função de suas ações e estados nos quais elas são tomadas. Isto acontece porque as recompensas não podem ser arbitrariamente alteradas pelo agente. Às vezes, o agente pode estar totalmente consciente do seu ambiente, mas ainda assim tem dificuldade em maximizar a recompensa, pois podemos saber como jogar o cubo de Rubik, mas ainda assim não podemos resolvê-lo. Portanto, podemos dizer com segurança que a relação agente-ambiente representa o limite do controle do agente e não o seu conhecimento.
A propriedade Markov
Transição : A mudança de um estado para outro é chamada Transição.
Probabilidade de Transição: A probabilidade de que o agente se mova de um estado para outro é chamada de Transition Probability.
O estado da propriedade Markov que :
“O futuro é independente do passado dado o presente”
Matematicamente podemos expressar esta afirmação como :
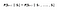
S denota o estado actual do agente e s denota o estado seguinte. O que esta equação significa é que a transição do estado S para S é totalmente independente do passado. Portanto, o RHS da Equação significa o mesmo que o LHS se o sistema tiver uma propriedade Markov. Intuitivamente significa que nosso estado atual já captura as informações dos estados passados.
Probabilidade de Transição do Estado :
Como agora sabemos sobre a probabilidade de transição, podemos definir a Probabilidade de Transição do estado da seguinte forma :
Para o Estado de Markov de S para S, ou seja qualquer outro estado sucessor , a probabilidade de transição de estado é dada por
Podemos formular a probabilidade de Transição de Estado numa matriz de probabilidade de Transição de Estado por :

Cada linha da matriz representa a probabilidade de passar do nosso estado original ou inicial para qualquer estado sucessor.A soma de cada linha é igual a 1,
Processo Markov ou Cadeias de Markov
Processo Markov é o processo menos aleatório da memória, ou seja, uma sequência de um estado aleatório S,S,….S com uma propriedade Markov. Portanto, é basicamente uma sequência de estados com a propriedade Markov. Pode ser definida usando um conjunto de estados(S) e matriz de probabilidade de transição (P).A dinâmica do ambiente pode ser totalmente definida usando a matriz de estados(S) e probabilidade de transição(P).
Mas o que significa processo aleatório ?
Para responder a esta pergunta vamos ver um exemplo:
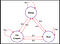
As bordas da árvore denotam probabilidade de transição. A partir desta cadeia vamos tirar alguma amostra. Agora, suponha que estivéssemos dormindo e de acordo com a distribuição de probabilidade haja uma chance de 0,6 de Fugir e 0,2 de dormir mais e novamente 0,2 de comer sorvete. Da mesma forma, podemos pensar em outras sequências que podemos amostrar desta cadeia.
algumas amostras da cadeia :
- Sleep – Run – Ice-cream – Sleep
- Sleep – Ice-cream – Ice-cream – Run
Nas duas sequências acima o que vemos é que obtemos um conjunto aleatório de estados(S) (i.e. Sleep,Ice-cream,Sleep ) cada vez que corremos a cadeia.Hope, agora está claro porque o processo Markov é chamado de conjunto aleatório de seqüências.
Before going to Markov Reward process let’s look at some important concepts that will help us in understand MRPs.
Reward and Returns
Rewards are the numerical values that the agent receives on performing some action at some state(s) in the environment. O valor numérico pode ser positivo ou negativo com base nas ações do agente.
No aprendizado do reforço, nos preocupamos em maximizar a recompensa cumulativa (todas as recompensas que o agente recebe do ambiente) ao invés de, o agente recebe do estado atual(também chamado de recompensa imediata). Esta soma total de recompensa que o agente recebe do ambiente é chamada de retorno.
Podemos definir Retornos como :
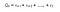
r é a recompensa recebida pelo agente no momento t enquanto executa uma ação(a) para se mover de um estado para outro. Da mesma forma, r é a recompensa recebida pelo agente no momento t ao executar uma ação para se mover de um estado para outro. E, r é a recompensa recebida pelo agente no último passo de tempo ao executar uma ação para se mover para outro estado.
Tarefas Episódicas e Contínuas
Tarefas Episódicas: Estas são as tarefas que têm um estado terminal (estado final). Podemos dizer que elas têm estados finitos. Por exemplo, em jogos de corrida, nós começamos o jogo (start the race) e o jogamos até que o jogo termine (corrida termina!). Isto é chamado um episódio. Assim que reiniciarmos o jogo ele começará de um estado inicial e, portanto, cada episódio é independente.
Continuous Tasks : Estas são as tarefas que não têm fim, ou seja, não têm nenhum estado terminal. Estes tipos de tarefas nunca terminarão. Por exemplo, Aprendendo a codificar!
Agora, é fácil calcular os retornos das tarefas episódicas, pois elas eventualmente terminarão, mas que tal tarefas contínuas, pois elas continuarão para sempre. Os retornos da soma até o infinito! Então, como definimos os retornos das tarefas contínuas?
É aqui que precisamos do Factor de Desconto(ɤ).
Factor de Desconto (ɤ): Determina quanta importância deve ser dada à recompensa imediata e às recompensas futuras. Isto basicamente ajuda-nos a evitar o infinito como recompensa em tarefas contínuas. Tem um valor entre 0 e 1. Um valor de 0 significa que é dada mais importância à recompensa imediata e um valor de 1 significa que é dada mais importância a recompensas futuras. Na prática, um factor de desconto de 0 nunca aprenderá, pois considera apenas a recompensa imediata e um factor de desconto de 1 continuará para recompensas futuras que podem levar ao infinito. Portanto, o valor óptimo para o factor de desconto situa-se entre 0,2 e 0,8.
Então, podemos definir retornos usando o fator de desconto da seguinte forma :(Digamos que esta é a equação 1, pois vamos usar esta equação mais tarde para derivar a Equação de Bellman)

Vamos entendê-lo com um exemplo,suponha que você vive em um lugar onde você enfrenta escassez de água, então se alguém vier até você e disser que vai lhe dar 100 litros de água!(assuma por favor!) para as próximas 15 horas em função de algum parâmetro (ɤ). Vamos olhar para duas possibilidades : (Digamos que esta é a equação 1, pois vamos usar esta equação mais tarde para derivar a Equação de Bellman)
Um com factor de desconto (ɤ) 0.8 :
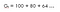
Isto significa que devemos esperar até a 15ª hora porque a diminuição não é muito significativa, por isso ainda vale a pena ir até ao fim, o que significa que também estamos interessados em recompensas futuras.Assim, se o fator de desconto é próximo de 1 então nós faremos um esforço para ir até o fim como a recompensa é de importância significativa.
Segundo, com fator de desconto (ɤ) 0.2 :
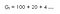
Isto significa que estamos mais interessados em recompensas antecipadas, pois as recompensas estão ficando significativamente baixas à hora. Assim, talvez não queiramos esperar até o final (até a 15ª hora), pois não valerá a pena. Assim, se o fator de desconto está próximo de zero, então as recompensas imediatas são mais importantes do que o futuro.
Então, qual o valor do fator de desconto a ser usado ?
Depende da tarefa para a qual queremos treinar um agente. Suponha que, em um jogo de xadrez, o objetivo é derrotar o rei do adversário. Se dermos importância às recompensas imediatas como uma recompensa pela derrota de um peão qualquer jogador adversário, então o agente aprenderá a realizar essas sub-gols, não importando se seus jogadores também forem derrotados. Portanto, nesta tarefa as recompensas futuras são mais importantes. Em alguns, podemos preferir usar recompensas imediatas como o exemplo da água que vimos anteriormente.
Processo de Recompensa Markov
Até agora vimos como a cadeia de Markov definiu a dinâmica de um ambiente usando um conjunto de estados(S) e Matriz de Probabilidade de Transição(P).Mas, sabemos que o Aprendizado de Reforço tem tudo a ver com o objetivo de maximizar a recompensa.Então, vamos adicionar recompensa à nossa cadeia de Markov.Isto nos dá Markov Reward Process.
Markov Reward Process : Como o nome sugere, os MDPs são as cadeias de Markov com julgamento de valores. Basicamente, nós recebemos um valor de cada estado em que nosso agente está.
Matematicamente, definimos Processo de Recompensa de Markov como :
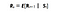
O que esta equação significa é o valor da recompensa (Rs) que recebemos de um determinado estado S. Isto nos diz a recompensa imediata desse estado em particular em que o nosso agente se encontra. Como veremos na próxima história como maximizamos essas recompensas de cada estado em que o nosso agente se encontra. Em termos simples, maximizando a recompensa cumulativa que recebemos de cada estado.
Definimos MRP como (S,P,R,ɤ),onde :
- S é um conjunto de estados,
- P é a Matriz de Probabilidade de Transição,
- R é a função de Recompensa, vimos anteriormente,
- ɤ é o factor de desconto
Processo de Decisão de Markov
Agora, vamos desenvolver a nossa intuição para a Equação de Bellman e Processo de Decisão de Markov.
Função Política e Função de Valor
Função de Valor determina o quão bom é para o agente estar em um determinado estado. É claro, para determinar o quão bom será para o agente estar em um determinado estado, ele deve depender de algumas ações que ele tomará. É aqui que entra a política. Uma política define que ações executar em um determinado estado s.

Uma política é uma função simples, que define uma distribuição de probabilidade sobre Ações (a∈ A) para cada estado (s ∈ S). Se um agente no momento t segue uma política π então π(a|s) é a probabilidade de que o agente com ação (a ) no momento (t). Em Reinforcement Learning a experiência do agente determina a mudança na política. Matematicamente, uma política é definida da seguinte forma :
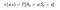
Agora, como encontramos um valor de um estado.O valor de estado s, quando o agente está seguindo uma política π que é denotada por vπ(s) é o retorno esperado a partir de s e seguindo uma política π para os próximos estados,até chegarmos ao estado terminal.Podemos formular isto como :(Esta função também é chamada de Função Valor do Estado)

Esta equação nos dá os retornos esperados a partir do(s) estado(s) e indo para os estados sucessores depois, com a política π. Uma coisa a notar é que os retornos que obtemos são estocásticos enquanto que o valor de um estado não é estocástico. É a expectativa de retornos do(s) estado(s) inicial(is) e depois dele(s) para qualquer outro estado. E também note que o valor do estado terminal (se houver algum) é zero. Vejamos um exemplo :
Suponha que o nosso estado inicial é a Classe 2, e depois passamos para a Classe 3 e depois para a Classe 2 > Classe 3 > Passar > Dormir.
Nosso retorno esperado é com fator de desconto 0,5:
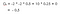
Nota:É -2 + (-2 * 0.5) + 10 * 0.25 + 0 em vez de -2 * -2 * 0.5 + 10 * 0.25 + 0.Então o valor da Classe 2 é -0.5 .
Função de Valor da Equação de Bellman
Função de Valor da Equação de Bellman ajuda-nos a encontrar políticas e funções de valor óptimas. Sabemos que a nossa política muda com a experiência para que tenhamos uma função de valor diferente de acordo com políticas diferentes.
A Equação de Bellman afirma que a função de valor pode ser decomposta em duas partes:
- Prémio imediato, R
- Valor descontado dos estados sucessores,
Matematicamente, podemos definir a Equação de Bellman como :
Vamos entender o que esta equação diz com a ajuda de um exemplo :
Suponha, há um robô em algum estado (s) e então ele se move deste estado para algum outro estado (s’). Agora, a questão é o quão bom foi para o robô estar no(s) estado(s). Usando a equação de Bellman, podemos dizer que é a expectativa de recompensa que ele recebeu ao sair do(s) estado(s) mais o valor do(s) estado(s) para o(s) qual(is) ele se moveu.
Vejamos outro exemplo :
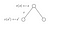
Queremos saber o valor dos estados s.O valor do(s) estado(s) é a recompensa que recebemos ao sairmos desse estado, mais o valor descontado do estado em que aterrissamos multiplicado pela probabilidade de transição em que nos moveremos para ele.
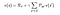
A equação acima pode ser expressa em forma de matriz da seguinte forma :

Onde v é o valor do estado em que estávamos, que é igual à recompensa imediata mais o valor descontado do estado seguinte multiplicado pela probabilidade de passar para esse estado.
A complexidade do tempo de execução para este cálculo é O(n³). Portanto, esta não é claramente uma solução prática para resolver MRPs maiores (o mesmo para MDPs também). Em Blogs posteriores, vamos olhar para métodos mais eficientes como Programação Dinâmica (Iteração de Valores e Iteração de Políticas), métodos Monte-Claro e TD-Learning.
Vamos falar sobre a Equação de Bellman em muito mais detalhes na próxima história.
O que é o Processo de Decisão de Markov ?
Processo de Decisão de Markov : É o Processo de Recompensa de Markov com uma decisão.Tudo é igual ao MRP, mas agora temos uma agência real que toma decisões ou toma ações.
É um tuple de (S, A, P, R, 𝛾) onde:
- S é um conjunto de estados,
- A é o conjunto de ações que o agente pode escolher para tomar,
- P é a Matriz de Probabilidade de transição,
- R é a Recompensa acumulada pelas ações do agente,
- 𝛾 é o fator de desconto.
P e R terá ligeira mudança nas ações w.r.t da seguinte forma:
Matriz de Probabilidade de Transição,
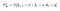
Função de Recompensa
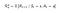 >
>
Agora, nossa função de recompensa depende da ação.
Até agora falamos em obter uma recompensa (r) quando nosso agente passa por um conjunto de estados (s) seguindo uma política π.Na verdade, no Processo de Decisão Markov (MDP) a política é o mecanismo para tomar decisões. Assim, agora temos um mecanismo que escolherá tomar uma ação.
Políticas em um MDP depende do estado atual. Elas não dependem do histórico. Essa é a propriedade Markov. Então, o estado atual em que estamos caracteriza o histórico.
Já vimos como é bom para o agente estar em um determinado estado (função valor do estado). Agora, vamos ver como é bom tomar uma determinada ação seguindo uma política π do estado s (função valor-ação).
Função valor-ação do estado ou Q-Função
Esta função especifica o quão bom é para o agente tomar uma ação (a) em um estado (s) com uma política π.
Matematicamente, podemos definir a função valor de estado-ação como :

Basicamente, diz-nos o valor de realizar uma determinada ação(a) em um(s) estado(s) com uma política π.
Vejamos um exemplo do Processo de Decisão de Markov :
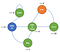
Agora, podemos ver que não há mais probabilidades.Na verdade agora o nosso agente tem escolhas a fazer como depois de acordar, podemos escolher assistir netflix ou código e debug. É claro que as ações do agente são definidas w.r.t alguma política π e será obtido a recompensa em conformidade.