
Embora, como mencionado na seção Análise de fluxo de sinal, alguma forma de análise de fluxo de sinal seja a forma mais geral de tratar o amplificador negative-feedback, a representação como duas portas é a abordagem mais frequentemente apresentada em livros didáticos e é apresentada aqui. Ele retém uma partição do circuito de dois blocos do amplificador, mas permite que os blocos sejam bilaterais. Alguns inconvenientes deste método são descritos no final.
Aplicadores eletrônicos usam corrente ou tensão como entrada e saída, então quatro tipos de amplificadores são possíveis (qualquer uma de duas entradas possíveis com qualquer uma de duas saídas possíveis). Veja a classificação dos amplificadores. O objetivo para o amplificador de feedback pode ser qualquer um dos quatro tipos de amplificador e não é necessariamente o mesmo tipo que o amplificador de laço aberto, que pode ser qualquer um desses tipos. Assim, por exemplo, um amplificador op (amplificador de voltagem) pode ser arranjado para fazer um amplificador de corrente ao invés disso.
Aplicadores de feedback negativo de qualquer tipo podem ser implementados usando combinações de redes de duas portas. Existem quatro tipos de rede de duas portas, e o tipo de amplificador desejado dita a escolha de duas portas e a seleção de uma das quatro diferentes topologias de conexão mostradas no diagrama. Estas conexões são normalmente referidas como conexões em série ou shunt (paralelas). No diagrama, a coluna da esquerda mostra as entradas de derivação; a coluna da direita mostra as entradas em série. A linha superior mostra as saídas em série; a linha inferior mostra as saídas de derivação. As várias combinações de conexões e duas portas estão listadas na tabela abaixo.
| Aplicador de alimentação tipo | Conexão de entrada | Conexão de saída | Retroalimentação de derivação | Dois-feedback da porta | |
|---|---|---|---|---|---|
| Corrente | Shunt | Série | CCCS | Parâmetro g | |
| Transistência | Shunt | Shunt | Shunt | CCVS | y-parâmetro |
| Transcondutância | Série | Série | VCCS | z-parâmetro | |
| Tensão | Série | Shunt | VCVS | h-parameter |
Por exemplo, para um amplificador de alimentação de corrente, a corrente da saída é amostrada para feedback e combinada com a corrente na entrada. Portanto, o feedback é realizado idealmente usando uma fonte de corrente controlada por corrente (saída) (CCCS), e sua realização imperfeita usando uma rede de duas portas também deve incorporar um CCCS, ou seja, a escolha apropriada para a rede de feedback é uma rede de duas portas com parâmetros g. Aqui é apresentado o método de duas portas usado na maioria dos livros didáticos, usando o circuito tratado no artigo sobre modelo de ganho assimptótico.

Figure 3 mostra um amplificador de dois transístores com um resistor de realimentação Rf. O objetivo é analisar este circuito para encontrar três itens: o ganho, a impedância de saída olhando para o amplificador a partir da carga, e a impedância de entrada olhando para o amplificador a partir da fonte.
- Substituição da rede de realimentação por uma porta de duas portasEdit
- Circuito de pequeno sinalEditar
- Ganho de circuito abertoEdit
- Ganho com feedbackEditar
- Resistências de entrada e saídaEditar
- Fundo na determinação da resistênciaEditar
- Aplicação ao amplificador de exemploEditar
- Tensão de carga e corrente de cargaEditar
- O bloco principal do amplificador é uma porta de duas portas?Edit
Substituição da rede de realimentação por uma porta de duas portasEdit
O primeiro passo é a substituição da rede de realimentação por uma porta de duas portas. Quais componentes vão para as duas portas?
No lado de entrada das duas portas temos o Rf. Se a voltagem no lado direito do Rf muda, muda a corrente em Rf que é subtraída da corrente que entra na base do transistor de entrada. Ou seja, o lado de entrada das duas portas é uma fonte de corrente dependente controlada pela tensão no topo do resistor R2.
Um poderia dizer que o segundo estágio do amplificador é apenas um seguidor de tensão, transmitindo a tensão no coletor do transistor de entrada para o topo do R2. Ou seja, o sinal de saída monitorado é realmente a voltagem no coletor do transistor de entrada. Essa visão é legítima, mas então o estágio do seguidor de voltagem torna-se parte da rede de realimentação. Isso torna a análise da realimentação mais complicada.
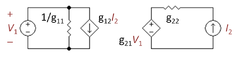
Uma visão alternativa é que a tensão no topo do R2 é definida pela corrente emissora do transistor de saída. Esta vista conduz a uma rede de realimentação totalmente passiva composta por R2 e Rf. A variável que controla a realimentação é a corrente do emissor, portanto a realimentação é uma fonte de corrente controlada por corrente (CCCS). Nós pesquisamos através das quatro redes de duas portas disponíveis e encontramos a única com um CCCS é a de dois parâmetros g, mostrada na Figura 4. A próxima tarefa é selecionar os parâmetros g de modo que as duas portas da Figura 4 sejam eletricamente equivalentes à seção L composta por R2 e Rf. Essa seleção é um procedimento algébrico feito mais simplesmente olhando para dois casos individuais: o caso com V1 = 0, que faz do VCVS no lado direito das duas portas um curto-circuito; e o caso com I2 = 0. que faz do CCCS no lado esquerdo um circuito aberto. A álgebra nestes dois casos é simples, muito mais fácil do que resolver todas as variáveis ao mesmo tempo. A escolha dos parâmetros g que fazem com que as duas portas e a secção L se comportem da mesma forma é mostrada na tabela abaixo.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\frac {\frac {\f}{R_{\mathrm {\f} }+R_{2}}}}
 |
– R 2 R 2 + R f {\i1}displaystyle -{\i}{R_{2}}{R_{2}+R_{\i}mathrm {f} }}}}
 |
R 2 R 2 + R f {\frac {\frac {R_{\f}}{R_{\f}+R_{\mathrm {\f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
{\i1}displaystyle R_{2}//R_{\i}mathrm {f} Figura 5: Circuito de pequeno sinal com duas portas para rede de realimentação; caixa sombreada superior: amplificador principal; caixa sombreada inferior: duas portas de realimentação substituindo a secção L composta por Rf e R2.
Circuito de pequeno sinalEditarO próximo passo é desenhar o esquema de pequeno sinal para o amplificador com as duas portas no lugar usando o modelo híbrido de pinos para os transistores. A Figura 5 mostra o esquema com a notação R3 = RC2 // RL e R11 = 1 / g11, R22 = g22. Ganho de circuito abertoEditFigure 3 indica o nó de saída, mas não a escolha da variável de saída. Uma escolha útil é a saída de corrente de curto-circuito do amplificador (levando ao ganho de corrente de curto-circuito). Como esta variável leva simplesmente a qualquer outra escolha (por exemplo, tensão de carga ou corrente de carga), o ganho da corrente de curto-circuito é encontrado abaixo. Primeiro o ganho do circuito aberto carregado é encontrado. A realimentação é desligada ajustando g12 = g21 = 0. A idéia é descobrir quanto o ganho do amplificador é alterado por causa dos resistores na rede de realimentação por eles mesmos, com a realimentação desligada. Este cálculo é bastante fácil porque R11, RB e rπ1 estão todos em paralelo e v1 = vπ. Deixe R1 = R11 // RB // rπ1. Além disso, i2 = -(β+1) iB. O resultado para o ganho de corrente em circuito aberto AOL é: A O L = β i B i S = g m R C ( β β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . A_{\i1}displaystyle A_{\i1}mathrm {\i} Tradução: Equipa PT-Subs “i_mathrm {m}}=g_{m}R_{\i1}mathrm {C} Esquerda (esquerda) (R_Frac) + R_Frac (direita) (R_R_1) (R_22) + R_Frac (ppp 2) + R_mathrm (C) …beta +1}}}}right…  Ganho com feedbackEditarNa abordagem clássica ao feedback, o feedforward representado pelo VCVS (ou seja, g21 v1) é negligenciado. Isso faz com que o circuito da Figura 5 se pareça com o diagrama de blocos da Figura 1, e o ganho com feedback é então: A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB} Frac 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 A_A_mathrm }}}}  A F B = A O L 1 + R 2 R 2 + R f A O L , {\i1}displaystyle A_{\i1}mathrm {FB} Frac 1+{\a1}{R_{\a2}}{R_{\a2}+R_{\a2} A_mathrm  onde o fator de feedback βFB = -g12. Notação βFB é introduzida para o fator de realimentação para distingui-lo do transistor β. Resistências de entrada e saídaEditar Figura 6: Configuração do circuito para encontrar a resistência de entrada do amplificador de realimentação
> Feedback é usado para melhor combinar as fontes de sinal com suas cargas. Por exemplo, uma conexão direta de uma fonte de tensão a uma carga resistiva pode resultar em perda de sinal devido à divisão de tensão, mas a interseção de um amplificador de realimentação negativo pode aumentar a carga aparente vista pela fonte e reduzir a impedância aparente do driver vista pela carga, evitando a atenuação do sinal por divisão de tensão. Esta vantagem não se restringe aos amplificadores de tensão, mas melhorias análogas na correspondência podem ser organizadas para amplificadores de corrente, amplificadores de transcondutância e amplificadores de transresistência. Para explicar estes efeitos da realimentação sobre impedâncias, primeiro uma digressão sobre como a teoria de duas portas se aproxima da determinação da resistência, e depois sua aplicação ao amplificador em questão. > Fundo na determinação da resistênciaEditarFigure 6 mostra um circuito equivalente para encontrar a resistência de entrada de um amplificador de tensão de realimentação (esquerda) e para um amplificador de corrente de realimentação (direita). Estes arranjos são aplicações típicas do teorema de Miller. No caso do amplificador de tensão, a tensão de saída βVout da rede de realimentação é aplicada em série e com uma polaridade oposta à tensão de entrada Vx que percorre o laço (mas em relação à terra, as polaridades são as mesmas). Como resultado, a tensão eficaz através e a corrente através da resistência de entrada do amplificador Rin diminui para que a resistência de entrada do circuito aumente (pode-se dizer que o Rin aparentemente aumenta). Seu novo valor pode ser calculado pela aplicação do teorema de Miller (para tensões) ou das leis básicas do circuito. Assim, a lei de tensão de Kirchhoff fornece: V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} +————————————————————————————————————————————————————————————————————————————————————————————————————————————–  where vout = Av vin = Av Ix Rin. Substituindo este resultado na equação acima e resolvendo para a resistência de entrada do amplificador de realimentação, o resultado é: R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . R_{\i1}displaystyle R_{\i}mathrm Fb)={\i1}frac {V_{x}{I_{x}}=esquerda(1++bbis A_v}direita)R_{\i1}mathrm }\ .} {\i1}displaystyle R_{\i} Fb)={\i1}frac {V_{x}{I_{x}}=esquerda(1++bbis A_v}direita)R_{\i1}mathrm A conclusão geral deste exemplo e um exemplo similar para o caso da resistência de saída é: Uma conexão de realimentação em série na entrada (saída) aumenta a resistência de entrada (saída) por um fator ( 1 + β AOL ), onde AOL = open loop gain.
Por outro lado, para o amplificador de corrente, a corrente de saída βIout da rede de realimentação é aplicada em paralelo e com direção oposta à corrente de entrada Ix. Como resultado, a corrente total que flui através da entrada do circuito (não apenas através da resistência de entrada Rin) aumenta e a tensão através dela diminui de modo que a resistência de entrada do circuito diminui (Rin aparentemente diminui). Seu novo valor pode ser calculado pela aplicação do teorema duplo de Miller (para correntes) ou das leis básicas de Kirchhoff: I x = V i n R i n + β i o u t . I_{{x}={\i1}frac {V_{\i}mathrm {\i} R_mathrm + + Beta i_mathrm }\ .}  where iout = Ai iin = Ai Vx / Rin. Substituindo este resultado na equação acima e resolvendo para a resistência de entrada do amplificador de realimentação, o resultado é: R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\\i1}displaystyle R_{\i}mathrm {\i} Fb)={\frac {V_{x}}{I_{x}}={\frac {R_{\mathrm {in} Esquerda(1+1+beta A_direita)}{\i} {\i1}displaystyle R_{\i}mathrm Fb)={\frac {V_{x}}{I_{x}}={\frac {R_{\mathrm {in} A conclusão geral deste exemplo e um exemplo similar para o caso da resistência de saída é: Uma conexão de feedback paralela na entrada (saída) diminui a resistência de entrada (saída) por um fator ( 1 + β AOL ), onde AOL = open loop gain.
Estas conclusões podem ser generalizadas para tratar casos com unidades arbitrárias de Norton ou Thévenin, cargas arbitrárias, e redes gerais de feedback de duas portas. No entanto, os resultados dependem do amplificador principal ter uma representação como uma porta dupla – ou seja, os resultados dependem da mesma corrente que entra e sai dos terminais de entrada, e da mesma forma, a mesma corrente que sai de um terminal de saída deve entrar no outro terminal de saída. Uma conclusão mais ampla, independente dos detalhes quantitativos, é que o feedback pode ser usado para aumentar ou diminuir a impedância de entrada e saída. Aplicação ao amplificador de exemploEditarEstes resultados de resistência agora são aplicados ao amplificador da Figura 3 e da Figura 5. O fator de melhoria que reduz o ganho, nomeadamente ( 1 + βFB AOL), decide diretamente o efeito do feedback sobre as resistências de entrada e saída do amplificador. No caso de uma conexão shunt, a impedância de entrada é reduzida por este fator; e no caso de uma conexão em série, a impedância é multiplicada por este fator. Entretanto, a impedância que é modificada pela realimentação é a impedância do amplificador na Figura 5 com a realimentação desligada, e inclui as modificações na impedância causadas pelos resistores da rede de realimentação. Por isso, a impedância de entrada vista pela fonte com o feedback desligado é Rin = R1 = R11 // RB // rπ1, e com o feedback ligado (mas sem feedforward) R i n = R 1 1 + β F B A O L , {\i1}displaystyle R_{\i}mathrm {\i} 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 A_A_mathrm  onde a divisão é usada porque a conexão de entrada é shunt: a porta de realimentação de duas portas está em paralelo com a fonte de sinal no lado de entrada do amplificador. Um lembrete: AOL é o ganho de circuito aberto carregado encontrado acima, como modificado pelos resistores da rede de realimentação. A impedância vista pela carga precisa de mais discussão. A carga na Figura 5 é conectada ao coletor do transistor de saída, e portanto é separada do corpo do amplificador pela impedância infinita da fonte de corrente de saída. Portanto, o feedback não tem efeito sobre a impedância de saída, que permanece simplesmente RC2 como visto pela resistência de carga RL na Figura 3. Se ao invés disso quiséssemos encontrar a impedância apresentada no emissor do transistor de saída (ao invés de seu coletor), que é uma série conectada à rede de feedback, o feedback aumentaria essa resistência pelo fator de melhoria ( 1 + βFB AOL). Tensão de carga e corrente de cargaEditarO ganho derivado acima é o ganho de corrente no coletor do transistor de saída. Para relacionar este ganho com o ganho quando a tensão é a saída do amplificador, observe que a tensão de saída na carga RL está relacionada com a corrente do coletor pela lei de Ohm como vL = iC (RC2 || RL). Consequentemente, o ganho de transresistência vL / iS é encontrado multiplicando o ganho de corrente por RC2 || RL: v L i S = A F B ( R C 2 ∥ R L ) . {\i1}displaystyle {\i}frac {v_{\i1}mathrm {\i} “i_mathrm A_{\an8}}=A_{\an8} R_mathrm displaystyle {\i}frac {v_mathrm {\i} “i_mathrm A_{\an8}}=A_{\an8} (R_{\mathrm {\C2}}}(R_{\mathrm {\L}}){4843>
Similiarmente, se a saída do amplificador for tomada como sendo a corrente na resistência de carga RL, a divisão da corrente determina a corrente de carga, e o ganho é então: i L i S = A F B R C 2 R C 2 + R L . {\displaystyle {\frac {\i_{\mathrm {\L} “i_mathrm A_{\an8}}=A_{\an8} “R”, “R”, “Mathrm”, “C2″… R_Mathrm {C2} + R_R_mathrm }}}\ .}  O bloco principal do amplificador é uma porta de duas portas?Edit Figura 7: Amplificador com ligações à terra etiquetado por G. A rede de realimentação satisfaz as condições de porta.
> Seguir-se-ão alguns inconvenientes da aproximação de duas portas, destinadas ao leitor atento. Figure 7 mostra o esquema de pequeno sinal com o amplificador principal e as duas portas de realimentação em caixas sombreadas. O feedback de duas portas satisfaz as condições de porta: na porta de entrada, Iin entra e sai da porta, e também na saída, Iout entra e sai. O bloco de amplificador principal também é uma porta de duas portas? O amplificador principal é mostrado na caixa sombreada superior. As conexões de terra são etiquetadas. A Figura 7 mostra o interessante fato de que o amplificador principal não satisfaz as condições de porta em sua entrada e saída a menos que as conexões de terra sejam escolhidas para fazer isso acontecer. Por exemplo, no lado da entrada, a corrente que entra no amplificador principal é IS. Esta corrente é dividida de três maneiras: para a rede de feedback, para o resistor de polarização RB e para a resistência de base do transistor de entrada rπ. Para satisfazer a condição de porta para o amplificador principal, todos os três componentes devem retornar ao lado de entrada do amplificador principal, o que significa que todos os cabos de terra marcados com G1 devem ser conectados, assim como o cabo emissor GE1. Da mesma forma, no lado da saída, todas as conexões de terra G2 devem ser conectadas e também a conexão de terra GE2. Então, na parte inferior do esquema, debaixo das duas portas de realimentação e fora dos blocos do amplificador, G1 é conectado a G2. Isso força as correntes de terra a se dividirem entre os lados de entrada e saída, conforme planejado. Note que esta disposição de conexão divide o emissor do transistor de entrada em um lado de base e um lado coletor – uma coisa fisicamente impossível de se fazer, mas eletricamente o circuito vê todas as conexões de terra como um nó, então esta ficção é permitida. O claro, a maneira como os cabos de terra estão conectados não faz diferença para o amplificador (eles são todos um nó), mas faz diferença para as condições de porta. Esta artificialidade é uma fraqueza desta abordagem: as condições de porta são necessárias para justificar o método, mas o circuito realmente não é afetado pela forma como as correntes são trocadas entre as conexões de terra. No entanto, se nenhuma disposição possível das condições de terra leva às condições de porta, o circuito pode não se comportar da mesma forma. Os fatores de melhoria (1 + βFB AOL) para determinar a impedância de entrada e saída podem não funcionar. Esta situação é estranha, porque uma falha em fazer uma porta dupla pode refletir um problema real (simplesmente não é possível), ou refletir uma falta de imaginação (por exemplo, simplesmente não pensou em dividir o nó emissor em dois). Como consequência, quando as condições da porta estão em dúvida, pelo menos duas abordagens são possíveis para estabelecer se os fatores de melhoria são precisos: ou simular um exemplo usando Spice e comparar resultados com o uso de um fator de melhoria, ou calcular a impedância usando uma fonte de teste e comparar resultados. Uma escolha mais prática é abandonar completamente a abordagem de duas portas, e usar várias alternativas baseadas na teoria do gráfico de fluxo de sinal, incluindo o método Rosenstark, o método Choma, e o uso do teorema de Blackman. Essa escolha pode ser aconselhável se os modelos de dispositivos de pequeno sinal forem complexos, ou não estiverem disponíveis (por exemplo, os dispositivos são conhecidos apenas numericamente, talvez a partir de medições ou de simulações SPICE). |